关于DVD在线租赁决策问题研究

(重庆交通大学经济与管理学院 重庆 400074)

一、引言与原始数据

(一)引言

随着信息时代的到来，网络成为人们生活中越来越不可或缺的元素之一。许多网站利用其强大的资源和知名度，面向其会员群提供日益专业化和便捷化的服务。例如,在线DVD租赁问题,即顾客缴纳一定数量的月费成为会员，订购DVD租赁服务。会员对哪些DVD有兴趣，只要在线提交订单，网站就会通过快递的方式尽可能满足要求。会员提交的订单包括多张DVD，这些DVD是基于其偏爱程度排序的。网站会根据手头现有的DVD数量和会员的订单进行分发。

(二)原始数据

现规定，每个会员每个月租赁次数不得超过2次，每次获得3张DVD。会员看完3张DVD之后，只需要将DVD放进网站提供的信封里寄回(邮费由网站承担)，就可以继续下次租赁，为了使在线DVD租赁更好的服务大众，我们需要对下列问题进行讨论。

1.网站正准备购买一些新的DVD，通过问卷调查和历史数据得到了会员对DVD的租赁情况。假设网站现有10万个会员，对表1中的每种DVD来说，在租赁公司的能力范围内，求解能保证希望看到该种DVD的会员中至少50%在一个月内能够看到该种DVD和三个月内至少95%的会员能够看到该种DVD应该准备的张数；

2.根据表2中列出的网站上100种DVD的现有张数和当前需要处理的1000位会员的在线订单，对这些DVD进行合理的分配，使会员获得最大的满意度并具体列出前30位会员(即C0001—C0030)获得的DVD的情况。

3.在表2的基础上假设表2中DVD的现有数量全部为0。如果你是网站经营管理人员，在考虑公司收益的情况下，决定每种DVD的购买量。

4.如果你是网站经营管理人员，明确提出在DVD的需求预测、购买和分配中其他的值得研究的重要问题并建立相应的数学模型。

表1 对1000个会员调查的部分结果

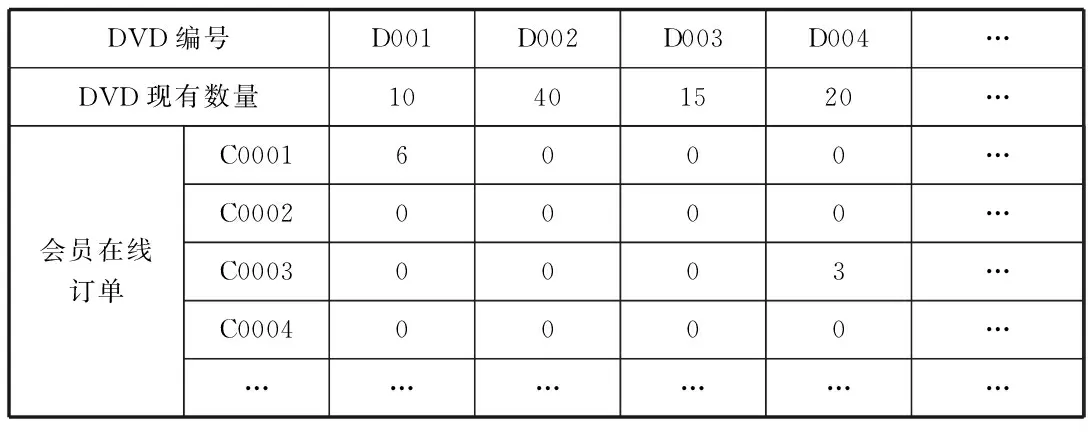
表2 现有DVD张数和当前需要处理的会员的在线订单

二、模型的假设与符号的约定

(一)模型的假设与说明

(1)假设每个月都是30天。

(2)假设每月租赁DVD一次的会员的租赁与归还日期介于每月1—30号之间，每月租赁DVD两次的会员的租赁与归还日期介于每月1—15号和16—30号 之间。

(3)假设每一位会员第一次租的碟片和第二次租的碟片完全不相同。

(4)假设碟片邮寄回来后不影响下一次租赁。

(5)不考虑DVD在租赁过程中的丢失、破损等情况。

(二)符号的约定与说明

X1每月租赁DVD一次的会员

X2每月租赁DVD两次的会员

E(X1) 每月租赁一次的会员所租赁的DVD的平均流通天数

E(X2) 每月租赁两次的会员所租赁的DVD的平均流通天数

E(X) 两种情况下碟片的平均流通天数

E1(X) 每张碟片一个月内的平均流通天数

E3(X) 每张碟片三个月内的平均流通天数

xij第i位会员选择第j种碟片

pij第i位会员对第j种碟片的满意度

Cij每种碟片的满意度

B总的碟片的满意度

S总的应该购买的碟片数

bj每种碟片应该购买的碟片数

三、问题的分析

(一)问题1的分析

对于问题一主要是解决在已知会员的人数的情况下，要使网站以准备最少的5种类型DVD的张数，来保证希望看到各种DVD的会员中至少50%在一个月内能够看到该DVD和至少95%的会员在三个月内能够看到该DVD这两个问题，利用概率论中均匀分布的相关知识可以解决该类问题。根据已知，首先确定两种租赁方式下碟片的平均流通天数，再按照两种租赁方式下会员的比例，可以确定每张碟片的平均流通天数，再根据每种碟片愿意观看的会员人数就可以确定每种碟片应该准备多少张。

(二)问题2的分析

对于问题二是对表2给出的100种DVD现有张数以及1000位会员的订单数对DVD进行分配，使会员获得最大的满意度，可建立0—1整数规划模型来进行处理，其中各名会员是否获得了各DVD类型为0—1变量，又因为会员的满意度跟会员的偏爱程度有关，表2中会员的在线订单数表示会员的偏爱程度，数字越小表示会员的偏爱程度越高，只需将会员所分配到不同种类的DVD所对应的订单数字求和取最小值，即满意度越大，所建立的目标函数的值越小。在这里又存在一个问题，由于数字0表示对应的DVD当前不在会员的在线订单中，所以为了避免出现结果为0的情况，我们把0改成100，这样就可以算出最小值从而达到对这些碟片进行合理的分配获得最大的满意度同时排除了结果不存在的可能性。

(三)问题3的分析

对于这个问题，本质上是双目标规划，我们采取逐步解决的方法，计算出DVD的购买量。对于第一小问如何决定DVD的购买量，我们注意到要购买满足题目要求的DVD张数，至少有950人可以得到满意的碟片，为此需要2850张碟片，又因为会员租赁碟片的情况有两种即一个月租赁一次和一个月租赁两次。要使一个月租赁两次的会员在第二次租赁时可以收到使自己满意的碟片，所以总共需要准备的碟片张数为2850+2850*0.4=3990张。在表2中会员对DVD的满意程度，由于数字越小，满意程度越大，因为有0的存在，为了避免结果不存在的情况(同问题2)，该题我们首先分别将表格中的1-10的对11的补数代替它们本身，这样数字越大就表示满意度越大，再分别求出每种碟片的满意度之和，然后求所有种碟片的总满意度，再根据每种满意度之和占总满意度的比例，就可以求得每种碟片的购买量。

(四)问题4的分析

因为大多数项目的最终目的就是为了盈利，为了更好的盈利和服务会员，每个月需要新增碟片，而在DVD在线租赁这个过程中，需要考虑到，碟片破损，会员逾期交费[1]等问题。因此我们想到的是在考虑这些不定因素的基础上计算当月的收益。

四、模型的建立与求解

(一)问题1的模型建立与求解

对于问题1，我们利用概率论中的均匀分布[2]，通过求数学期望得到两种租赁方式下每种碟片的平均流通天数以及两种比例下会员的租赁的碟片的平均流通天数：

通过得到的一个月内每张碟片的平均流通次数以及愿意观看的每种DVD的会员人数，根据表1，计算可得保证希望看到该DVD的会员中至少50%在一个月内能够看到该DVD至少应该准备的碟片数:

DDVD1=(200÷1000×100000×0.5)÷E1(X);

DVD2=(100÷1000×100000×0.5)÷E1(X);

DVD3=(50÷1000×100000×0.5)÷E1(X);

DVD4=(25÷1000×100000×0.5)÷E1(X);

DVD5=(10÷1000×100000×0.5)÷E1(X);

最终结果为:

DVD1≈3704;

DVD2≈1852;

DVD3≈926;

DVD4≈463;

DVD5≈185;

同理可得为使在三个月内至少95%的会员能够看到该DVD应该准备的碟片张数:

(二)问题2的模型建立与求解

对于问题2，由于1位会员可以选择3张DVD，若第i位会员选择第j种DVD记为xij,则xij=1否则xij=0;其中i=1…1000;j=1…100;pij表示会员对某种DVD的偏爱程度[3](数字越小，表示偏爱程度越大)。为此建立0-1整数线性规划模型：

首先利用表格中的数据，然后编写lingo程序求解模型，为了方便结果解释，最后将前30位会员(即C0001-C0030)分别获得哪些DVD输入到表3。如下所示表格中30行表示的是30位会员所分配到的碟片情况，第一列表示的是30位会员，第二列表示的是选择情况。

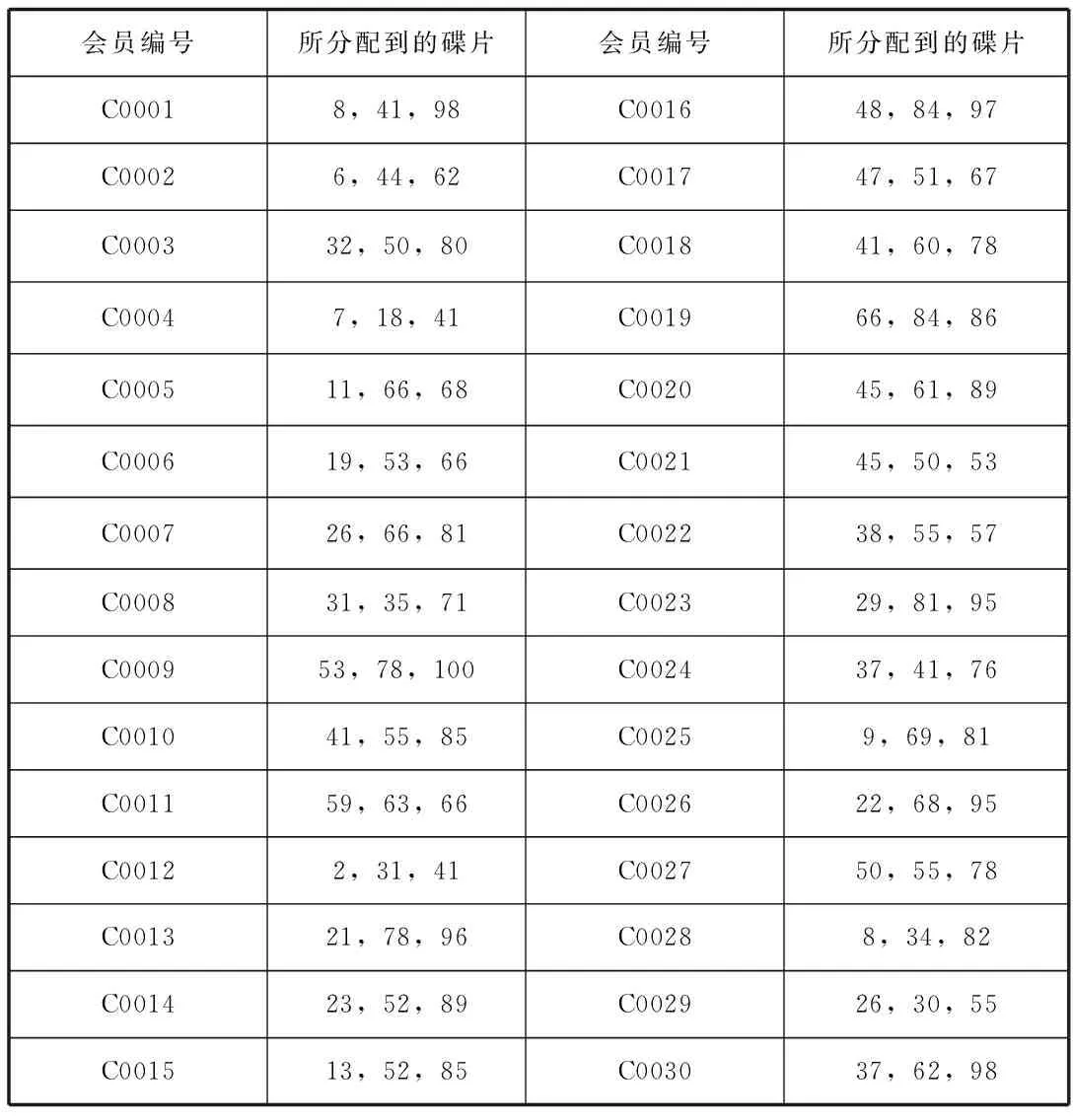
表3 会员所获得的碟片种类

(三)问题3的模型建立与求解

为了求得DVD的购买量，我们根据题目要求，因为一共有1000名会员，所以至少有950名可以获得自己满意的DVD，一次可以获得三张，又因为每月租赁一次的会员在每月租赁两次的会员进行第二次租赁时碟片不一定邮寄回来，为了使一个月租赁两次的会员可以看到网站购买的所有碟片，所以网站一共需要购买S=2850+2850×0.4=3990张碟片，确定了碟片总数，利用11这个数字将满意度扩大化，接下来需要根据每种碟片的满意度[4]占总体的比例，来求得每种碟片应该购买的数量。为此建立如下的数学模型：

利用Matlab编程求得每种DVD的购买量，如下图所示：

图1 D0001—D0020种碟片的购买量

图2 D00021—D0040种碟片的购买量

图3 D00041—D0060种碟片的购买量

(四)问题4的模型建立

假设当月购买第i种DVD的数量为ai,价格为bi,则当月购买DVD所花费的总金额为：

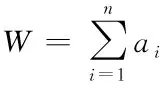
假设会员的数量E与会费c和会员的满意程度h有关，建立如下关系式：

E=f(c,h);

会员的满意程度h与可选择的DVD的数量n和种类d有关：

h=f(d,n);

假设DVD的损坏数量D可表示为：D=λE;

假设损毁DVD的单价y为所有DVD单价的平均价格：

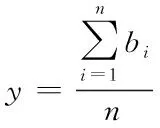
假设每月盈利Q与会员会费，购买DVD的价格和DVD的亏损费用有关。根据以上建立如下单目标规划模型：

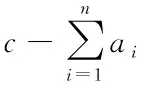
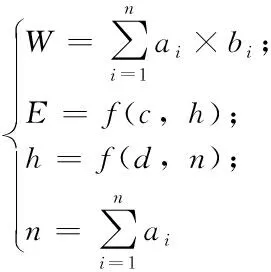
五、模型的进一步讨论

对于问题3的第二问，我们在计算时仅仅考虑了一次租赁的情况，没有按照历史数据显示的规律分为两种情况考虑，为此我们进行了如下的模型改进。

新增符号及说明：yij表示二次租赁时会员i选择第j种碟片。具体的数学模型如下所示:

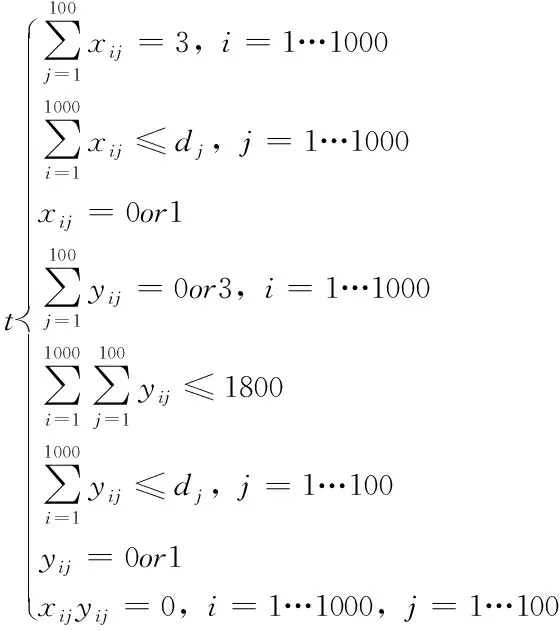
表示会员要么进行1次租赁，要么进行2次租赁，且两次均会获得三张碟片，如果进行二次租赁的话，所需碟片张数按照会员总数的60%进行计算。

六、模型的优缺点

(一)优点

(1)建立的规划模型能与实际紧密联系起来，结合实际情况对问题进行求解，使模型具有很好的通用性和推广性，比如在一些商品的销售过程中同样可以使用该类数学模型。(2)模型的计算采用专业的数学软件，可信度高，可操作性强。(3)对表格中的数据进行了处理，让建模和编程的过程变得简单方便。

(二)缺点

(1)由于是调查问卷所抽取的会员，导致数据有一定的局限性，建立的模型不一定适用于所有会员。(2)数据量太大，表格数据量大，计算容易出错。(3)计算项目多，联系性大，容易在分析过程中出现错误，导致全局出错。