基于改进集的集值优化问题的全局真有效性*

潘铭敏， 仇秋生

(浙江师范大学 数理与信息工程学院,浙江 金华 321004)

0 引 言

集值优化理论是最优化理论与应用的主要研究领域之一.随着最优化理论在经济均衡、决策博弈等领域的发展,集值优化的重要性日益得到体现.由于集值优化问题的有效解(弱有效解)是关于偏序为非劣意义下的解,这种解集一般都很大,甚至还包含一些性质比较差的解.因此,如何缩小有效解的范围一直是集值优化的重要课题.近年来,人们相继提出了各种真有效性,主要有Benson真有效性、超有效性和全局真有效性[1]等.值得注意的是,上述真有效性是基于拓扑线性空间提出的,这一特性在许多实际问题中不一定能得到满足.因此,将真有效性的概念和性质推广到线性空间具有重要的意义.在线性空间中,文献[2]提出了弱有效解的概念并利用择一性定理给出了弱有效解的最优性条件;文献[3]提出了向量闭集的概念,相对于代数闭集,向量闭集更加贴近拓扑闭集的性质;文献[4]定义了向量优化问题的Benson真有效解,并给出其标量化定理;文献[5]研究了集值优化问题的近似Henig真有效性.另一方面,由于集值优化模型是各种实际问题中的抽象，对模型的求解本身就是一种近似的过程,因此,近似真有效性的研究对解决实际问题具有重要的价值和意义.文献[6]提出改进集的概念并建立了E-有效解,它包含有效解、弱有效解、近似弱有效解等作为特殊情况;文献[7]将改进集从有限维空间推广到局部凸空间.在此基础上,文献[8]引入了近似E-次类凸集值映射的概念,并给出E-Benson真有效解的最优性条件.改进集的特性使得它为集值优化问题统一解的讨论提供了有效的途径.如何将集值优化问题的真有效性推广到更一般的线性空间,并提出统一的全局真有效性,具有理论和实际意义.

在文献[3,6-9]的基础上,本文利用改进集和线性空间中的代数性质,提出一类更加广泛并且不需要拓扑结构的E-全局真有效性,试图将一些精确和近似的全局真有效解进行统一研究,并且通过凸集分离定理获得了集值优化问题E-全局真有效解的最优性条件.

1 预备知识

若无特别申明,以下总设X,Y,Z是实序线性空间,Y*,Z*分别表示Y和Z的代数共轭空间.A是Y中的任一非空子集,0表示每个空间中的零元.K是Y的非空子集.若∀k∈K,λ≥0,有λk∈K,则称K为锥.K的锥包定义为coneK:=∪{λk:λ≥0,k∈K}.若锥K还是凸集,则称K为凸锥.若K∩(-K)={0},则称K为点锥.锥K是非平凡的当且仅当K≠{0}且K≠Y.

K⊂Y的对偶锥K+和严格对偶锥K+i定义如下:

K+:={y*∈Y*|〈y,y*〉≥0,∀y∈K};

K+i:={y*∈Y*|〈y,y*〉>0,∀y∈K{0}}.

以下均假设K为凸锥.

定义1[7]设E是Y中的非空子集,若0∉E且E+K=E,则称E是关于锥K的改进集,简称E是改进集,记Y中所有改进集的集合为ζY.

定义2[3]若A是Y中的非空子集,则称

corA:={a∈A|∀y∈Y,∃λ′>0,∀λ∈[0,λ′],a+λy∈A},

vclA:={a∈A|∃y∈Y,∀λ′>0,∃λ∈(0,λ′],a+λy∈A},

linA:=A∪{x∈Y|∃a∈A,[a,x)⊂A}

分别为A的代数内部、向量闭集和代数闭集.

注1由定义2可得到以下包含关系:

1)corA⊆A; 2)A⊆linA⊆vclA.

引理1[10]设K是Y中代数内部非空的凸锥.若E∈ζY,则corE=E+corK.

引理2[11]若A是Y中的非空凸集,则对∀x1∈corA,x2∈linA,有[x1,x2)⊂corA.

命题1设A是代数内部非空的凸集,则A+=(corA)+.

证明 因为corA⊆A,所以A+⊆(corA)+.

下证(corA)+⊆A+.事实上,对∀ψ∈(corA)+,有

〈a1,ψ〉≥0, ∀a1∈corA.

因为A⊂linA,所以由引理2知,∀a2∈A,有[a1,a2)⊂corA.因此,对∀t∈(0,1],有

ta1+(1-t)a2=a2+t(a1-a2)∈corA.

由于ψ∈(corA)+,所以〈a2+t(a1-a2),ψ〉≥0,∀a1∈corA,∀a2∈A.当t→0+时,〈a2,ψ〉≥0,∀a2∈A,即ψ∈A+.因此, (corA)+=A+.命题1证毕.

定义3[9]设A是Y中的非空子集,F:A→2Y为集值映射,K是Y中的凸锥.若vcl(cone(F(A)+K))在Y中是凸集,则映射F在A上是近似K-次类凸的.

定义4设A是Y中的非空子集,E∈ζY,F:A→2Y是集值映射.若vcl(cone(F(A)+E))是凸集,则映射F在A上是近似E-次类凸的.

注2当corK⊆E⊆K时,vcl(cone(F(A)+E))=vcl(cone(F(A)+corK))=vcl(cone(F(A)+K)).此时,线性空间上的近似E-次类凸集值映射就是近似K-次类凸的.但近似E-次类凸映射不一定全是近似K-次类凸映射.

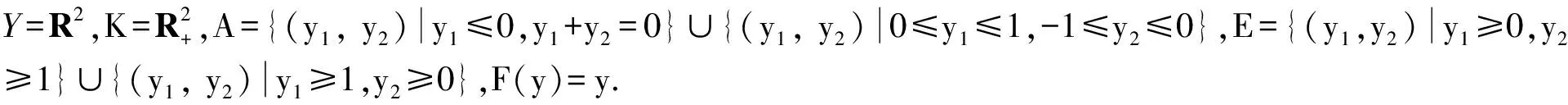
引理3[2]设K是Y中代数内部非空的凸锥.若y∈corK,且y*∈K+{0},则〈y,y*〉> 0.

引理4[11]设A,B是2个非空凸集,corA≠Ø,且(corA)∩B=Ø,则A和B可用超平面分离.

2 E-全局真有效性的代数性质

下面给出实序线性空间中基于改进集的全局真有效点的定义,其次说明该定义的合理性,最后讨论E-全局有效点与其他真有效点之间的关系.

首先引入线性空间中的近似和精确全局真有效点的概念.

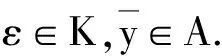
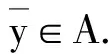
注3线性空间中集合的全局真有效点也具有平移性质.

命题2设A是Y中的非空子集,K⊂Y为凸锥,则G(A,K)=G(A+K,K).

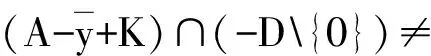
下证G(A+K,K)⊆G(A,K).

对∀y′∈G(A+K,K),存在点凸锥D满足K{0}⊆corD,使得(A-y′+K)∩(-D{0})=Ø.由于A⊂A+K,所以

(A-y′)∩(-D{0})=Ø.

(1)

假设y′∉A,由y′∈G(A+K,K)⊂A+K知,存在a∈A,a≠y′,使得y′-a∈K{0}⊂corD⊂D{0}.故a-y′∈-D{0},与式(1)矛盾.因此,y′∈A.结合式(1)知,y′∈G(A,K).从而G(A+K,K)⊆G(A,K).命题2证毕.

下面给出实序线性空间中基于改进集的全局真效性的定义.

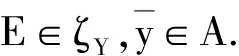
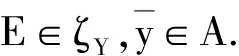
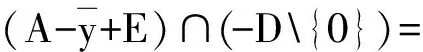
(2)

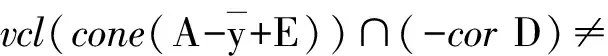
(3)

已知d∈-corD,则d∈cor(-corD).对式(3)中的y1,存在λ′>0,∀λ∈[0,λ′],有d+λy1∈-corD.因为λn→0+,所以存在充分大的n0∈N,使得λn0∈[0,λ′].因此,

d+λn0y1∈-corD.

(4)

注4线性空间中基于改进集的全局真有效性是一个很广泛的概念,E-全局真有效性对一些精确和近似全局真有效性进行了统一,例如:

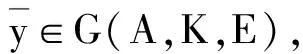
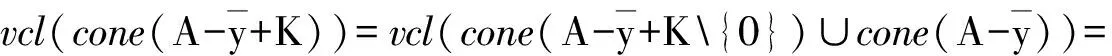
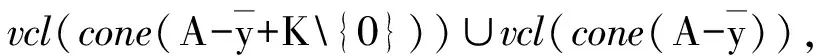
(5)

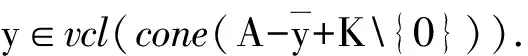
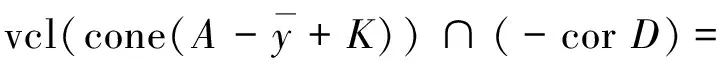
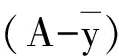
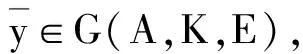
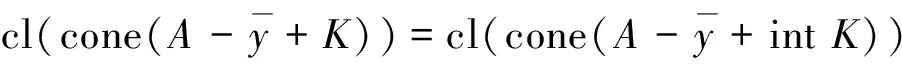
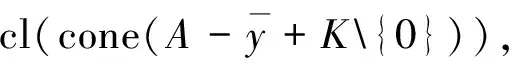
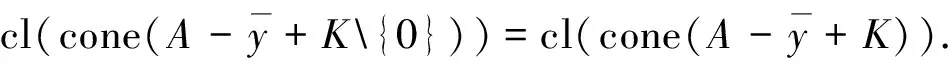
下面引入E-有效点和E-Benson真有效点的定义,讨论E-全局真有效点和它们之间的关系.

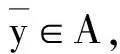
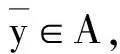
命题4设E∈ζY,A⊂Y为非空子集,则

1)G(A,K,E)⊆E(A,K,E); 2)G(A,K,E)⊆B(A,K,E).

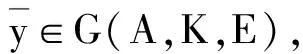
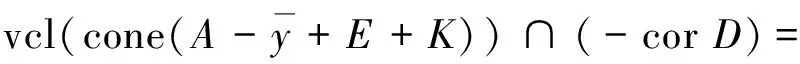
Ø.

(6)

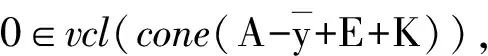
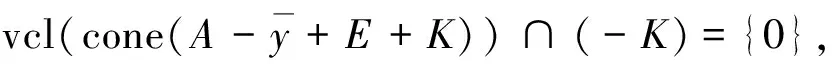
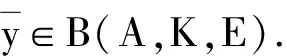
注5命题4中1)的逆命题不一定成立,即G(A,K,E)真包含于E(A,K,E).

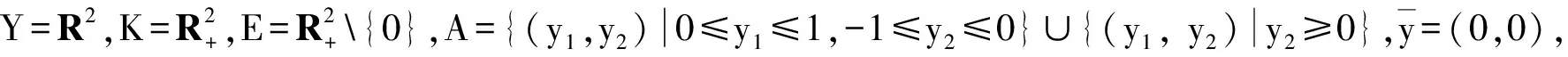
3 集值优化问题E-全局真有效解的最优性条件

下面给出集值优化问题E-全局真有效解的概念,其次讨论E-全局真有效解的标量化特征和Lagrange乘子定理.

设S⊂X是非空子集,F:S→2Y和G:S→2Z是2个集值映射,K和P分别是Y与Z中的凸锥.

考虑如下集值优化问题:

其中,W={x∈S|G(x)∩(-P)≠Ø},称W为(VP)的可行集.

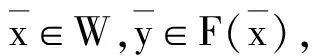
由(VP)诱导的标量优化问题如下:

其中,φ∈Y*{0}.

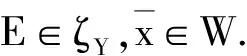
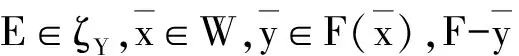
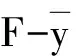
当式(7) 中的r =0 时，〈d，φ〉≥0，∀d∈cor D.因此，φ∈(cor D)+.由命题1知，φ ∈D+{0} .而K {0}⊂cor D，所以由引理3 知〈k，φ〉> 0，∀k∈K {0} ，即φ∈K+i.将式( 7) 中的d 固定，有

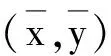
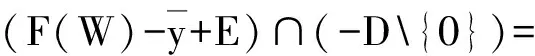
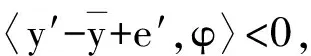
注7当E=ε+K,ε∈K{0}时,定理2就退化为文献[9]中的定理4.2.

下面给出线性空间中集值优化问题的Lagrange乘子定理.设L(Z,Y)是由空间Z到Y的所有连续线性算子组成的集合,记L+(Z,Y)={T∈L(Z,Y)|T(P)⊆K}.

考虑由(VP)诱导的无约束集值优化问题:

其中,T∈L+(Z,Y).

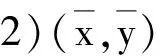
3)H(x)在S上是近似E×P-次类凸的,

⊆(corK∪{0})(corE).

cone(H(W)+E×P)∩(-cor(D×P))=Ø.

显然,cone(H(S)+E×P)∩(-cor(D×P))=Ø.由命题3可得

vcl(cone(H(S)+E×P))∩(-cor(D×P))=Ø.

由条件3)知,vcl(cone(H(S)+E×P))在Y×Z上是非空凸集,又cor(D×P)在Y×Z上也是非空凸的,所以由引理4知,存在(y*,z*)∈(Y*,Z*)(0,0),使得∀r≥0,x∈S,p1∈P,(y,z)∈F(x)×G(x),(d,p)∈cor(D×P),e∈E,

(9)

下面分3步进行证明.

1)证明y*∈K+i.在式(9)中令p1=0,则

(10)

令式(10)中的r=0,有〈d,y*〉+〈p,z*〉≥0,∀(d,p)∈cor(D×P).因D和P都是锥,故y*∈(corD)+,z*∈(corP)+.由命题1知,(y*,z*)∈(D×P)+.固定式(10)中的d和p,可得

当r→∞时，有

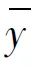
(11)

下证y*≠0.假设y*=0,则z*≠0.因此,式(11)可简化为

〈z,z*〉≥0, ∀x∈S,z∈G(x).

(12)

(13)

因为(cone(G(S)+P))+=(vcl(cone(G(S)+P)))+,所以z*∈(vcl(cone(G(S)+P)))+=Z+,从而〈z,z*〉≥0,∀z∈Z.由于Z是线性空间,∀z∈Z,有-z∈Z,所以〈-z,z*〉≥0.进一步可得z*=0,这与假设矛盾.因此,y*≠0,即y*∈D+{0}.由于K{0}⊆corD,所以〈k,y*〉>0,∀k∈K{0}.这表明y*∈K+i.

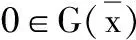
-〈e,y*〉≤〈z′,z*〉≤0, ∀e∈E.

(14)

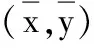
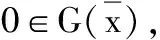
所以

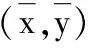
注8定理3推广了文献[12-13]中关于集值优化问题全局真有效解的Lagrange乘子定理.

1)当E=ε+K,ε∈K{0}时,文献[13]中的定理3.1就是定理3的特殊情况;

2)当Y是局部凸的拓扑线性空间时,若-int(D×P)是非空的,则近似E×P-次类凸就等价于ic-E×P-类凸,取E=K{0}时，定理3就退化为文献[12]中的定理3.1.

4 结 语

利用改进集,将集值优化问题的全局真有效解从局部凸的拓扑线性空间推广到实序线性空间.提出集值优化问题的E-全局真有效性,统一了全局真有效性和近似全局真有效性等概念.通过凸集分离定理,获得了线性空间中E-全局真有效解在目标函数为近似E-次类凸下的最优性条件.同时,给出了具体的例子,阐述一些概念和结论之间的关系.可以看出,线性空间中集值优化问题的E-全局真有效解具有广泛性和一般性.