单边Lipschitz时滞系统的H∞函数观测器设计*

周诚来， 蔡秀珊

(浙江师范大学 数理与信息工程学院,浙江 金华 321004)

0 引 言

实际生活和工程应用中,时滞现象常引起系统的不良反应甚至破坏系统的稳定性,因此希望对时滞系统设计一个控制器，使之稳定[1-3].另一方面,系统的状态估计也是控制研究的一大主题.外部未知干扰的存在不仅影响系统本身的状态变化,更影响了状态观测的准确性.Kalman滤波法[4]与H∞滤波法[5]是常用的两类观测器设计方法.值得注意的是,若用H2范数作为系统的性能指标,特别是存在不确定项或者外部干扰的系统,将不能保证其鲁棒性.因此,本文考虑设计一类H∞观测器.

对于非线性系统,渐进观测器可以精确地估计系统的状态[6-14].现有观测器设计大多针对于满足Lipschitz条件的一类非线性系统,设计方法存在保守性,因而,2006年文献[15]提出了单边Lipschitz概念.此后对单边Lipschitz及准单边Lipschitz系统的观测器设计得到了一些研究成果[16-20].

然而,对于非线性时滞系统满足单边Lipschitz条件的H∞函数观测器设计还未见报道.因此,本文考虑设计一类可有效抑制外部干扰的非线性时滞系统的H∞函数观测器.同时,还希望所设计的观测器具有灵活性：既可以是全维的，也可以是降维的.对于降维的观测器,则期望寻求一种简单的设计,且能通过统一的观测器设计算法得到.研究成果将与一类Lipschitz非线性观测器[21]作比较.

1 系统描述

考虑如下非线性时滞系统:

(1)

式(1)中:x∈Rn,u∈Rm,y∈Rp分别为系统的状态、输入和输出;xτ(t)是x(t)的滞后时间为τ的滞后状态;ω(t)∈Rs为外部噪声或干扰;A∈Rn×n,B∈Rn×n,C∈Rp×n,D1∈Rn×s,D2∈Rp×s为已知实矩阵;函数Φ(x,u):Rn×Rm→Rn是分别关于变量x,u连续的非线性函数.本文假定(A,C)可观测,且C为行满秩矩阵,初始条件ψ(t)在区间[-τ,0]上连续,并要求非线性函数Φ(x,u)满足以下2个条件：

定义1(单边Lipschitz条件[15]) 设O为包含原点的区域,若存在ρ∈R,使得对∀x1,x2∈O,有

〈Φ(x1,u)-Φ(x2,u),x1-x2〉≤ρ‖x1-x2‖2,

(2)

则称非线性函数Φ(x,u)满足单边Lipschitz条件.其中,称标量ρ为单边Lipschitz常数,可取正值、负值或0.

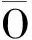
(Φ(x1,u*)-Φ(x2,u*))T(Φ(x1,u*)-Φ(x2,u*))≤

β‖x1-x2‖2+γ〈Φ(x1,u*)-Φ(x2,u*),x1-x2〉,

(3)

则称非线性函数Φ(x,u)满足二次内部有界条件.其中,称标量β,γ为二次内部有界常数.

2 H∞函数观测器设计

2.1 观测器形式

针对系统(1),考虑如下形式的观测器:

(4)

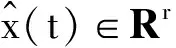
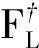
由系统状态x(t)和观测器状态ξ(t)得到观测误差为

ε(t)=ξ(t)-Tx(t).

(5)

对式(5)两边关于t求导,得到ε(t)的动态方程

(HT-TB)xτ(t)+TΔΦ+Dω(t).

(6)

式(6)中:

(7)

D=MD2-TD1.

(8)

且得到估计状态为

(9)

若待定矩阵满足下列3个等式：

NT+MC=TA,

(10)

HT=TB,

(11)

GT+FC=FL,

(12)

即

(13)

则由式(6)和式(9)得

(14)

式(14)中,e(t)为观测状态与系统实际状态之间的观测误差.

2.2 待定矩阵可解性

对于方程(13)解的存在性问题,可利用矩阵方程理论和矩阵广义逆[22]的相关性质定理.对于负定(半负定)矩阵Y,记作Y<0(Y≤0).

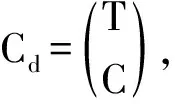
(15)

式(15)中:TG∈Rn×r;CG∈Rn×p.于是

(16)

秩条件1

(17)

若方程(13)满足秩条件1且Δ2为列满秩矩阵,则方程(13)存在可行解.并且

(18)

式(18)中,Y1,Y2,Y3为任意r×(r+p)维实矩阵.

(19)

最后得到观测器中各待定矩阵的表达式：

(20)

3 主要结果

这一节,基于线性矩阵不等式(linear matrix inequality,LMI)理论,主要解决系统(1)的H∞观测器设计问题,即观测误差应满足以下2个性质：

性质1在ω(t)=0时,观测误差e(t)=Gε(t)能渐近收敛于平衡点.由表达式易知,当误差系统状态ε(t)渐近收敛于平衡点时,e(t)也渐近收敛于平衡点.

性质2在ω(t)≠0时,∀ω(t)∈L2[0,∞),在假设误差动态系统的初始状态为0的情况下,ε(t)=0,∀t∈[-τ,0],且对于任意给定的μ>0满足H∞性能指标

‖e(t)‖2<μ‖ω(t)‖2.

以下是本文的主要结果:

定理1若非线性函数Φ(x,u)满足式(2)和式(3),并且存在标量τ1,τ2>0,2个正定矩阵P,Q和适当维数的矩阵N,M,H,G和F,使得式(13)有解且满足

(21)

证明 取Lyapunov-Krasovskii泛函

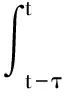
(22)

令ζ=(ε(t),ετ(t),ΔΦ,ω(t))T,则V沿着误差动态系统(14)轨线的导数为

ε(t)TQε(t)-ετ(t)TQετ(t)=

(23)

由非线性函数满足单边Lipschitz条件(2)得

则∃τ1>0,有

(24)

同理,因非线性函数满足二次内部有界条件(3),故∃τ2>0,有

(25)

令

(26)

将式(26)的右端与式(24)和式(25)的左端相加,利用条件(21)得J≤0,即

(27)

对于式(27),当干扰ω(t)=0时,根据Lyapunov稳定性定理知误差系统渐近稳定.因此,性质1成立.当干扰ω(t)≠0时,对式(27)两边积分后得

(28)

由于H∞性能指标条件下要求误差动态系统为零初始状态,即ε(t)=0,∀t∈[-τ,0],故V(0)=0,于是

‖e(t)‖2<μ‖ω(t)‖2.

从而性质2成立.定理1证毕.

定理1中的矩阵不等式(21)并不是一个LMI,目前不能在MATLAB LMI toolbox中求解.这是因为矩阵的(1,1)位置中含有2个矩阵变量的乘积项NTP和PN.下面分析如何将矩阵不等式(21)转化为线性矩阵不等式.

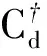
令X=PY1,则

(29)

为线性的.

于是得到如下基于定理1的LMI：

(30)

式(30)中,Σ11如式(29)所示.

经过前面的理论分析,证明了本文所设计的观测器的存在性.下面的算法将具体给出本文所设计的观测器的计算步骤.

算法1

步骤1：给定行满秩矩阵FL∈Rr×n,选取合适的矩阵T∈Rr×n,判断秩条件1,若满足,则进入下一步,否则重新选取矩阵T.

步骤3：给定适当的Y3,由式(20)中的第3,4,5式确定G,F和H.

步骤4：对于给定的衰减度μ>0,解LMI(30),若式(30)有解P,X,τ1,τ2,则进入步骤5,否则调整T,重回步骤1.

步骤5：得到Y1=P-1X,并且通过式(20)的第1,2式得到M,N.系统(1)的H∞观测器设计完毕.

4 算例仿真

本文所设计的观测器既可以是全维的也可以是降维的,因此在算例仿真中,笔者安排2个对比方案来验证本文观测器的有效性.例1为全维观测器与文献[21]的对比,例2为全维与降维观测器之间的对比.

例1全维观测器比较

文献[21]中机器人模型的状态空间描述如下：

其中:Jm,Jl,θm,θl,ωm,ωl分别代表电机的转动惯量、连杆的转动惯量、电机转动角位移、连杆角位移、电机转动角速度和连杆角速度;m表示机器人质量;h表示连杆长度;g为重力加速度;k,B,Kτ为模型转换系数.考虑如下非线性时滞模型：

y(t)=Cx(t)+D2ω(t).

干扰信号如图1所示.

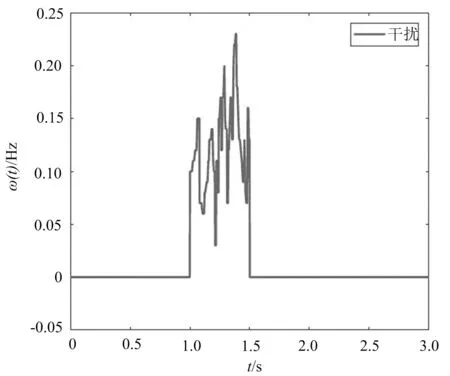
图1 外部干扰信号

由于非线性函数Φ(x,u)满足单边Lipschitz条件和二次内部有界条件,故可选取一组(ρ,β,γ)=(-9,11.088 9,-1),利用算法1,得到相应的增益矩阵分别为：

H=I4;

且得到对应的正数τ1=0.422 6,τ2=0.258 9.

用本文设计的观测器分别观测机器人的电机转动角位移和连杆角位置,结果如图2所示.

图2 电机转动角位移和连杆角位置的真实值与观测值

图3 针对电机的不同观测器观测效果对比

图4 针对连杆的不同观测器观测效果对比

定理1推论2[21]电机转动角位移观测误差对比θm的误差上界/radθm的误差下界/rad5.614 3-0.124 27.000 0-7.620 8连杆角位移观测误差对比θl的误差上界/radθl的误差下界/rad5.579 6-8.991 422.950 8 -24.581 0增益矩阵数量级比较10kk=2k=3误差收敛时间/s(‖e‖≤1)0.975 01.112 5

注2文献[21]中的系统模型并未考虑外部干扰信号输入的情况,本文设计的观测器不仅考虑了上述情况,观测效果也比较好.

例2降维与全维观测器比较

本例用机器人的模型,比较本文设计的降维观测器与全维观测器之间的区别.降维观测器设计方法如下：

同样选取几项指标,对于全维观测器和降维观测器的数据比较记录在表2中.对于收敛时间的统计,选取误差精度为0.1,提取介于稳定在[-0.1,0.1]的初始点.

图5 状态ωm的实际值和观测器及观测误差

图6 状态ωl的实际值和观测器及观测误差

图7 状态θl的实际值和观测器及观测误差

指标ωm的误差上界/(rad5s-1)ωm的误差下界/(rad5s-1)ωl的误差上界/(rad5s-1)ωl的误差下界/(rad5s-1)θl的误差上界/(rad5s-1)θl的误差下界/(rad5s-1)收敛时间/s误差ωm误差ωl误差θl全维2.881 5-2.401 22.630 5-2.073 01.231 34.145 75.635 112.581 912.581 9降维0.791 4-0.249 11.414 5-0.201 30.215 2-0.025 71.552 711.841 612.095 5

由表2可知,在例2中,相对于全维观测器,降维观测器能更快地观测到被挑选的系统状态.并且误差的上下界更小.

5 结 语

本文基于一类有干扰的时滞非线性系统设计H∞函数观测器.利用矩阵方程组和Lyapunov稳定性理论得到了误差系统的渐近稳定.所设计的观测器既可以是全维也可以是降维的.研究成果应用到了一类机器人观测器设计.