二步迭代法在中心仿射Hölder条件下的收敛性*
2018-11-23徐秀斌周文静
徐秀斌, 周文静
(浙江师范大学 数理与信息工程学院,浙江 金华 321004)
0 引 言
设X,Y是Banach空间,D⊆X是一个非空开凸子集,F:D⊆X→Y为非线性算子,且有连续的Fréchet导数F′,本文考虑非线性算子方程
F(x)=0
(1)
的求解问题.求解上述非线性算子方程最经典的方法是Newton法,取定初始点x0∈D,其迭代过程为
xk+1=xk-F′(xk)-1F(xk),k=0,1,….
(2)
在非线性算子F的一阶Fréchet导数连续且满足Lipschitz条件的情况下,Newton法的收敛阶为2.由于广泛的应用背景,众多学者对Newton法的收敛性做了大量研究,得到了各种收敛条件,如文献[1-5]中所述.
文献[4]给出了L平均的径向Lipschitz条件:
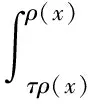
(3)

文献[5]在文献[4]的基础上提出了更一般的L平均仿射径向Hölder条件:
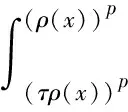
(4)
在条件(4)下证明了Newton法(2)的局部收敛性,得到了收敛阶为1+p和解的唯一性.
有些学者对Newton法进行了修正,如文献[6-10]研究了如下的二步迭代法:
(5)
受以上文献启发,本文假定F′,F″分别满足L平均中心仿射Hölder条件和L平均Lipschitz条件:
(6)
式(6)中:x,y∈B(x*,r);ρ(x)=‖x-x*‖;p∈(0,1];L1,L2是正的单调非减可积函数.本文将利用条件(6)证明方法(5)的局部收敛性,并给出收敛阶和解的唯一性.
1 局部收敛性分析
为证明局部收敛性定理,先引入如下引理,其中的1)和2)引自文献[10],3)引自文献[5].
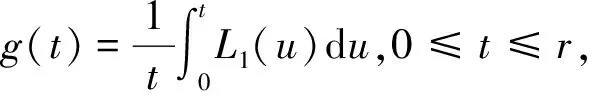

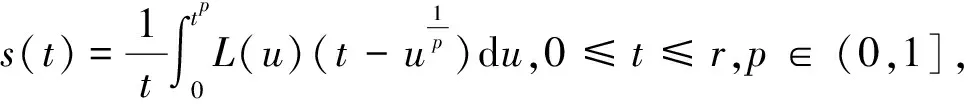
定理1设F(x)是一个非线性算子,D是非空开凸子集,F:D⊆X→Y.假定
1)F(x)=0有解x*∈D,F′(x*)存在且可逆;
2)在B(x*,r)⊂D内F′,F″存在,且分别满足L平均中心仿射Hölder条件和L平均Lipschitz条件(6);
3)r>0且满足

(7)
4)r0,r1∈(0,r),并且是下面方程组的解:
(8)
进一步,其误差估计满足:
(9)

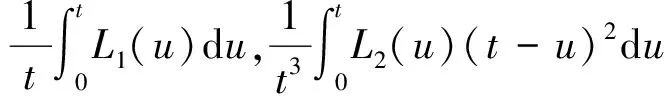
设x,y∈B(x*,r),则由式(6)和式(7)可得

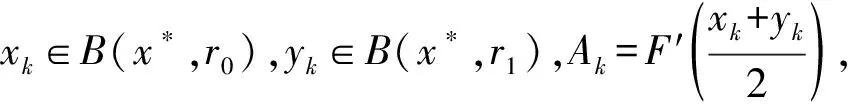
(10)
由文献[10]中的引理1得
故
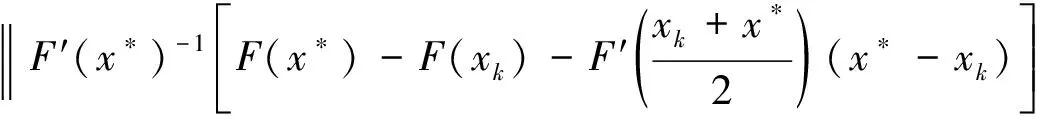
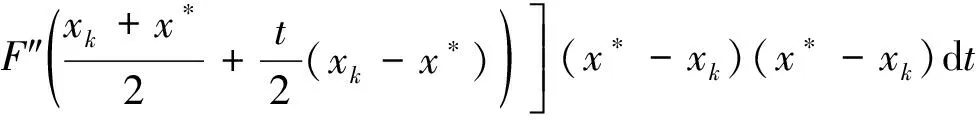
且
根据引理1、式(6)和式(7)有
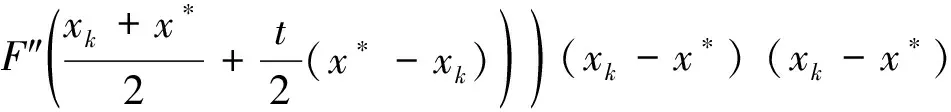
所以,
‖xk+1-x*‖≤
(11)
因此,
(12)
式(12)中,Zk=ρ(xk)+ρ(yk)+ρ(xk+1).式(11)说明数列{‖xk-x*‖}单调递减且有界,所以极限存在.下证其极限为0.设极限为α(0≤α 下证R收敛阶.由式(11)和式(12)可得: ρ(xk+1)≤Jρ(xk)3+Cρ(xk)ρ(yk)p,k=0,1,2,…; ρ(yk+1)≤[Jρ(xk+1)2+E(ρ(xk)+ρ(yk)+ρ(xk+1))p]ρ(xk+1)≤ 定理2假设F(x*)=0,F在B(x*,r)内有连续的导数,F′(x*)-1存在,且F′满足L平均中心仿射Hölder条件 其中:ρ(x)=‖x-x*‖;L是正的非减可积函数.若r满足 则方程F(x)=0在B(x*,r)的解唯一. 证明 对任意的x0∈B(x*,r),引入迭代法 xk+1=xk-F′(x*)-1F(xk),k=0,1,2,…, (13) 则 x1-x*=x0-x*-F′(x*)-1(F(x0)-F(x*))=F′(x*)-1[F′(x*)(x0-x*)-F(x0)+F(x*)]. 因此,当ρ(x0)≠0时, 其中, 由数学归纳法易证 方程组(8)有一组解为r1≈0.32,r2≈0.49,且x0∈B(x*,r0),y0∈B(x*,r1).在今后的工作中可考虑怎样简化定理1的条件.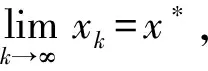

2 解的唯一性
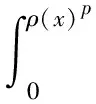
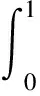
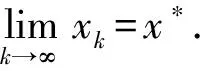
3 结 语