圆柱与其展开图

刘善娜（特级教师）

【教学时机】

人教版六年级下册《圆柱的认识》学习之后，圆柱的表面积、体积学习之前。

【教学目标】

1.通过画圆柱与其展开图的草图，使学生进一步掌握圆柱的特征。

2.通过图形的“动态展开”，让学生感受面与体的关联，帮助其理解抽象的数据转换。

【教学过程】

一、回顾特征

师：这两天，我们认识了圆柱，谁来说说它们有什么特征？

（板书：两个底面，一个侧面，无数条高，直柱体）

【设计意图：通过对圆柱外部特征的回顾，为学生画草图做好知识准备。】

二、尝试画圆柱

1.明了“草图”。

师：同学们能试着在纸上画一个圆柱的草图吗？

要求：数据不必准确，也不必用作图工具，但是要让大家能看出这是一个圆柱，要具备圆柱的基本特征。（板书：不必精确，但需具备基本特征）

【设计意图：学生通过对作图“要求”的解读，加深对草图的认识。】

2.学生尝试作图。

3.展示交流。

投影呈现圆柱草图，指认底面、侧面、底面周长、高、直径，并标上字母d和h。

三、从“立体”到“平面”

1.尝试画展开图。

师：这个圆柱（如上图），如果沿着h将它的侧面展开，会是什么形状？（长方形）既然侧面展开是长方形，决定它的大小的就是——长和宽。长和宽分别怎么画？请你试一试，要求展开图的大小尽可能符合要求。

【设计意图：在实际学习过程中，我们经常发现学生能口答“侧面的长就是底面周长，侧面的宽就是圆柱的高”，但是在具体转化应用时却又一筹莫展。学生对立体与平面之间的转化仅仅停留在动态展示的理解中，而没有深入地去感受过转化中的数据关系。让学生画大小尽可能符合数据要求的侧面展开图，是需要学生从关系的角度展开深度地思考，而不仅仅是简单地画一个长方形。】

2.展示汇报。

●展示一：大概估计，心里没有估的标准。

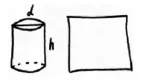
师：看着他画的圆柱与侧面展开图，你从展开图的长和宽两个维度去观察，有什么想说的吗？

追问1：他画的宽度超过了圆柱的高，那我们在草图上应该如何确定展开图的宽呢？

追问2：长方形的长，自然比圆柱底面的直径要长，但到底是多长？与圆柱底面的直径之间有什么关系？为什么是π倍的关系？（展开图的长，就是圆柱的底面周长）

●展示二：虑及π倍的草图。

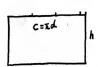
师：谁能看明白他这个草图的画法？这三个分割点代表什么意思？每一段代表什么意思？

【设计意图：在这一展示过程中，从“大概估计”的作品切入，暴露不关切具体数据的问题，再展示关注了具体数据的作品，通过“你能看明白吗？”达成互动交流，为改进作图做好准备。】

3.再画巩固。

（1）实物动态，辅助理解。

结合侧面展开图的草图，将一张A4纸卷成的圆柱侧面展开，指认圆柱的底面周长和高分别变成了长方形的长和宽，理解草图中的立体图与平面图之间的联系。

（2）从直径出发，画一个侧面展开图。

根据草图中圆柱的底面直径长度，画出侧面展开图的长，根据圆柱的高，画出侧面展开图的宽。

（3）补充展开图。

师：这是一个圆柱侧面的展开图，你能根据展开图将圆柱的两个底面添上去吗？圆柱的底面的大小如何确定？

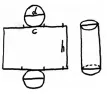
小结：从侧面展开图的长中，确定直径的大概程度，就能画底面的圆。

四、从“平面”到“立体”

1.学会确定圆柱的底面直径和高。

师：如果现在有这样一张长方形的纸，你能画出它左右相卷，卷成圆柱体后的草图吗？如何确定圆柱的底面直径和高？

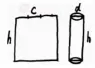
小结：长方形的宽就是圆柱的高，而将长方形的长分成三份多余一点的形式，其中的一份就是圆柱底面直径的长度。

2.学会画长方形纸从两种方向卷成圆柱的草图。

师：请利用给你的两个长方形草图继续来画。

要求：（1）配上底面。不同方向卷起来的两种底面。

（2）画出对应的圆柱。

（3）同桌交流方法，集体小结。

【设计意图：通过已知的长方形的平面图形画立体的圆柱草图，进一步把握侧面展开图的长与圆柱底面直径的关系，帮助学生建立相互转化的连接。】

3.特殊的侧面。

师：如果圆柱的侧面展开图是一个正方形，说明什么？

生：底面周长=高。

师：你能根据这个侧面展开图画出圆柱吗？

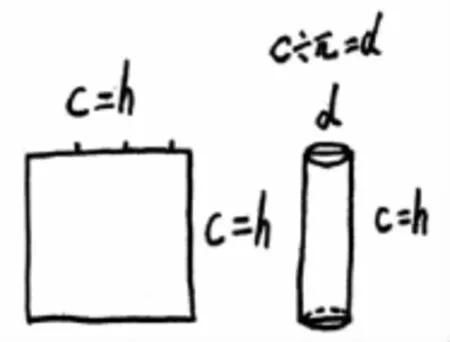
师：如果现在告诉你圆柱的侧面展开是一个边长为2cm的正方形，看谁画的圆柱草图最接近准确数据。（允许用尺子测量）

师：谁来说说你是如何让自己的草图接近准确数据的？

小结：侧面展开图的正方形边长2cm→底面周长2cm→（分成三份多一点）底面直径→高2cm。

【设计意图：通过侧面展开图为正方形的特殊圆柱，让学生画接近准确数据的草图，用数据估着画，能使学生进一步把握正方形的边长与圆柱的底面直径、高的联系。】

五、全课总结

师：这节课，画了圆柱和它的展开图，你有什么收获？圆柱的大小和它的侧面展开图密切相关，有哪些具体的数据联系？

小结：从圆柱草图，画出较为准确的侧面展开图，从侧面展开图，画出较为准确的圆柱草图，最重要的就是找到它们之间的联系。

【教学建议】

本节课内容，重在帮助学生理解面、体转化中内在数据的关联。学生在后期解决问题中，经常遇到根据平面展开图的数据无法计算立体图形的表面积、体积，或者根据立体图形的数据无法解决平面展开图的相关问题。这份“画数学”教学内容，让学生通过画草图对其中的关系有了深度的理解。在实际教学中要关注两个重点：

一、直观感知要充分

在这节课画草图之前，要让学生有充分的直观感知。

1.认识圆柱时，可以给每位学生一张A4纸反复操作演示侧面的“面曲成体”，让学生指一指、说一说这张长方形的纸卷成圆柱后，它的长和宽分别变成了圆柱的什么。

2.认识圆柱后，可以让每位学生动手制作完整的纸质圆柱（可以利用学具纸片），不仅直观体验“面曲成体”，而且在两个底面贴合的过程中，感受到底面与侧面的关联。在学生制作完成后，要让学生在“侧面”和“底面”上分别指认“底面周长”，要抓住几个重点问题：“底面周长”怎么在“侧面”上也能找到？如果“侧面”的大小确定了，对“底面”有什么影响？如果“底面”的大小确定了，对“侧面”有什么影响？

有了这些感知，课堂上学生就能更顺利地在体到面、面到体中穿行往复，能更好地掌握较为准确地达成平面、立体互相转化的技巧，并理解其中的道理。

二、后续作业要跟进

这节课的画图内容变化较多，过程也较为复杂，建议作业跟进。如布置“一个圆柱的侧面展开是一个边长为5cm的正方形，请画出圆柱的草图，尽可能接近准确数据。（允许用尺子测量）”。也可以设计成“侧面展开是一个长8cm、宽6cm的长方形”，使答案多样化。