阅读质疑创新——《圆锥的体积》教学实践与思考

陈继辉

【教学内容】

浙教版六年级下册第68、69页。

【教学过程】

一、预习反馈，质疑揣摩

1.交流圆锥体积的推导。

预习单

（1）阅读课本，画一画关键信息。

（2）想一想：课本上的圆锥体积公式是怎么来的？

（3）你还有什么问题？

师：课前我们已经预习了，哪位同学来说说圆锥的体积是怎么推导的？

生：找一个等底等高的圆柱，通过用圆锥往圆柱中倒水正好倒满三杯的实验，推导出圆锥体积是圆柱体积的三分之一。

2.质疑揣摩。

师：为什么在研究圆锥体积时要选择用圆柱？

生：因为在已经学过的图形中，圆柱与圆锥比较接近，“长”得有点像。

师：那么圆锥的体积和什么有关？怎么想到与底和高有关？

生：我们发现当底不变高变化时，圆锥体积发生变化；当高不变底在变时，体积也发生变化。

师：大家有问题想问吗？

生：为什么要选择等底等高的圆柱呢？

生：控制变量越少，实验越好操作。其他量不变，只看两个变量之间的关系，便于研究。

师：很好，我们在研究问题时要学会去质疑。长方形、三角形旋转一周可以得到圆柱和圆锥，猜一猜、估一估圆柱和圆锥之间的体积关系。

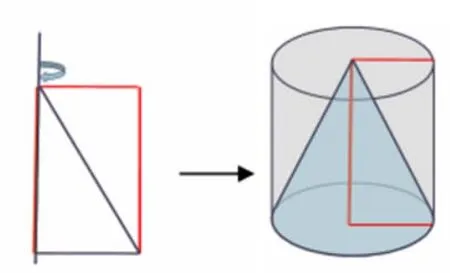
生：旋转得到了圆柱和圆锥，我估计圆锥的体积没有等底等高的圆柱体积的一半大。

3.实验操作。

教师演示：等底等高的圆柱与圆锥进行倒水实验演示。

师：等底等高的圆柱和圆锥，如果在圆锥中装满水，倒到圆柱中一次，圆柱中水的高度与圆柱的高是什么关系呢？

生：圆柱中水的高度是圆柱高的三分之一。

4.创新提升。

师：还有其他方法推导圆锥的体积公式吗？

生：我还可以通过倒沙子的实验进行推导。

生：我在课外书上见到过另外的方法，它是通过测量得到的。

师：我们在学习的过程中，不能只是接受，还要想想有没有其他的方法，要尝试创新。还有问题想问吗？

生：这个圆锥体积公式以前也是这样的吗？

师：这个问题提得真好！以前是不是这样的呢？现在和以前有没有什么不同呢？这就要求我们会质疑，包括质疑课本，这样的思考对学习很重要。

【设计意图：本环节让学生经历自主阅读学习，复述再现圆锥体积推导过程，并引导学生提问，感知圆锥体积与圆锥的高和底面积有关，估计圆锥体积与等底等高圆柱体积之间的关系；通过实验进一步明确圆锥体积与等底等高圆柱体积的关系。学生普遍已知圆锥体积公式及典型推导过程，在此基础上引导学生理解、质疑文本知识，培养发现问题、提出问题的能力，引发深度学习。】

二、阅读交流，拓展提升

1.阅读材料一。

师：我们来看看，古人是如何来推导圆锥体积公式的？请大家拿出学习单，自主阅读材料一。

（阅读要求：重点句画一画、关键词圈一圈、疑问处打问号）

我国古代劳动人民早在2000多年前，就会计算不同形状物体的体积。《九章算术》第五章《商功》中就记载了圆锥体积的计算方法是：“周自相乘，以高乘之，三十六而一”。“周自相乘”就是说底面周长乘以底面周长。“以高乘之”就是用圆柱的高来乘以刚才的积，“三十六而一”就是用刚才算出的结果再除以三十六。换字母来表示，半径用字母r表示，高用字母h表示，那么底面周长就是 2πr。“周自相乘”就是2πr×2πr，“以高乘之”就再乘以高，就是 2πr×2πr×h，最后“三十六而一”再除以 36，变成了2πr×2πr×h÷36。运用商不变性质，依次去除。圆锥体积是r×r×h。这个是由于当时π的取值为3，没有现在计算得那么精确。

师：有谁找出答案了？

生：古时候是用公式2πr×2πr×h÷36 来进行计算的。

师：你阅读很认真。老师还看到你用了圈一圈、画一画关键词句的方法，大家觉得怎么样？

生：这个方法真好。以后我们阅读时也要学着这样圈一圈、画一画。

师：古时候与现在两种算法，从最终结果看起来比较接近。你们还有什么问题想问吗？

生：这个体积公式是怎么来的？

生：为什么古时候用底面周长与高来算圆锥体积？这样计算对不对呢？

师：会去揣摩、质疑阅读内容了，给同学们点赞。

生：可能是古时候为了满足生活需要，测量不够准确。

生：因为周长与高比较好测量。

师：是的，以前结合生活实物，反复测量，取一个大概的数量就可以，没有精确度的要求。另外，我们要学会去质疑、揣摩课本上的结论以及公式推导过程。

【设计意图：在实际阅读的过程中，教师指导阅读，反思、点评阅读的方法，不仅在于“画一画重点，圈一圈关键词”以提炼信息，本质上要经历质疑、迁移和改造的思维过程，从而发展批判性思维能力。另一方面，拓展学习圆锥体积的数学文化背景，提升数学素养。】

2.阅读材料二。

师：同学们，节假日出去玩吗？看过金字塔吗？

生：看过，很好玩。

师：请同学们运用刚才阅读的方法，试着来阅读材料二。

埃及金字塔始建于公元前2600年以前，共有70多座，大部分位于开罗西南吉萨高原的沙漠中，是世界公认的“古代世界七大奇迹”之一。以胡夫金字塔最为出名。现高137米，塔的4个斜面正对东南西北四个方向。底部四边几乎是正北、正南、正东、正西，误差更少于1度。这般准确的方位绝不是偶然定出来的，考古学家认为是建筑师以右框星为指标定出来的。它的塔基呈正方形，每边长约230米。

（学生自主阅读，圈一圈、画一画重点词句）

师：谁来说说，你了解到了哪些信息？

生：我了解到胡夫金字塔的塔基是边长为230米的正方形，塔高137米。

（电脑演示胡夫金字塔的数学模型）

师：塔基呈正方形是什么意思？高是什么？

生：下底面是正方形，高是底面中心到顶点的距离。

师：有问题想提问吗？

生：四棱锥有什么特点？

生：四棱锥的体积怎么求？

师：先看第一个问题。四棱锥有什么特点？

生：四棱锥有一个顶点，底面是一个四边形，材料二中的四边形比较特殊是个正方形。

师：第二个问题，你们觉得怎么计算四棱锥的体积？

生：底面积乘高除以3。

生：四棱锥的体积公式一定是这样的吗？

生：这个公式是怎么来的？与圆锥体积公式的推导一样吗？

生：我觉得四棱锥体积公式可能要借助等底等高的长方体来推导。

师：你是怎么想到的？

生：因为在推导圆锥的体积公式时我们借助了等底等高的圆柱，所以，我觉得四棱锥可以借助等底等高的长方体。

师：到底是不是这样呢？我们可以有什么方法验证？

生：我们可以通过倒水的方法来验证。

（教师利用课件动画演示倒水实验）

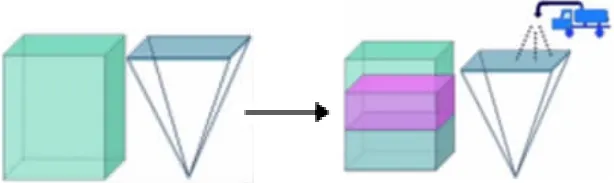
师：看来四棱锥的体积等于底面积乘高除以3，如果下底面变成五边形呢？它的体积可以怎么算？

生：底面积乘高除以3。

师：有问题问吗？

生：八边形呢？

生：也是底面积乘高除以3。

生：一直变大，n边形呢？

生：底面积乘高除以3。

师：底面边数不断变大，无限大，慢慢变成什么了？

生：底面变成了圆，整个图形变成了圆锥。

师：日常生活中，哪些地方见到过四棱锥？

生：螺丝刀口……

【设计意图：拓展、贯通图形知识，基于阅读材料，创设进一步提问研究的空间。由圆锥体积计算与推导，类比推理四棱锥的体积，利于学生形成联系的观点，发展类比推理能力。从四棱锥生发，想象、分析底面是正多边形直至圆形的锥体体积，从有限到无限，培养概括创新的能力，发展空间观念。】

三、课堂总结，回归整理

师：你有什么收获？我们是怎么学习的？

生：我们以后在预习课本的过程中，需要想一想书上的方法是怎么来的，为什么用这种方法？

生：我们要学着质疑数学课本上的结论，还要想一想有没有别的方法解决问题。

师：你们总结得真好！今天这节课我们先是用圈一圈、画一画等阅读方法，去揣摩书本编写意图，接着质疑书本结论，今后我们也要学着用这样的方法去解决数学问题。

【设计意图：本环节再现知识，整理、回顾学习的过程，培养学生反思、总结的能力，学会学习。】

【编辑点评】

《圆锥的体积》一课是在学生认识了长方体、正方体、圆柱体等立体图形，掌握了圆柱和圆锥的特征，会计算圆柱的表面积、体积的基础上进行教学的。以往教学一般只是引导学生在倒水实验的基础上进行公式推导，而本课设计不仅关注公式的由来，还有意选取了两则课外阅读材料作为引导学生阅读、质疑、拓展研究体积的课题，在相关的知识和方法之间有效地架起思考的桥梁，促进学生深度学习。

材料内涵丰富，可从多个层面解读。一是知识层面。阅读材料一，将古代算法与现代算法作比较，并通过演算转化，再次强化了基本计算公式阅读材料二，从圆锥迁移到棱锥，又从棱锥发展到圆锥，贯通有限和无限，实质是生成了对锥体体积计算的概括。二是思维层面。阅读材料一，理解不同算法，拓展学生思路，培养质疑好问的习惯；阅读材料二，则运用了类比推理的方法，实现计算知识和推导方法的迁移。三是学习信念层面。阅读材料一启示学生：运算公式并不是从天而降、刻板规定的，可以通过不同途径的探索得到，并逐步合理、优化、精准。而阅读材料二，则有利于学生形成联系的观点。

同时，陈老师注重学习内容与阅读方法紧密结合。学生通过自主阅读，经历比较、分析、推理、概括等思维过程，实现阅读理解水平从简单复述到深入概括，关注的不是文本的传递，而是借助文本来拓宽认知背景，引发对公式的深层理解，创设知识、方法应用的新空间，培养发现问题与提出问题、分析问题与解决问题的能力。