陷入循环，晕了？

王进

算法的三种基本结构——顺序结构、选择结构和循环结构中，循环结构相对其他两种结构而言，较难理解和掌握，以致不少同学常被循环转得头晕目眩！

循环结构有两种基本形式，一种是直到型循环（图1），另一种是当型循环（图2）.

这两种结构的逻辑顺序不同，直到型循环是先执行再判断，不满足条件时执行循环体，满足条件时结束循环；当型结构是先判断再执行，满足条件时执行循环体，不满足条件时结束循环.

两种结构可以相互转换，满足同样的意义.与两种结构相对应的伪代码有Do语句和While语句.

我们用循环结构及其伪代码解决问题时，主要涉及初始值、判断条件、循环体和终点值的设置，由于循环结构及其伪代码涉及的因素较多，同学们常常因判断和理解不到位，而导致一些错误.本文帮你厘清循环结构易出错的关键环节——初值、判断条件、循环体及终点值，让你神清气爽地面对循环，面不改色头不晕！

一、设置初始值不可急于求成

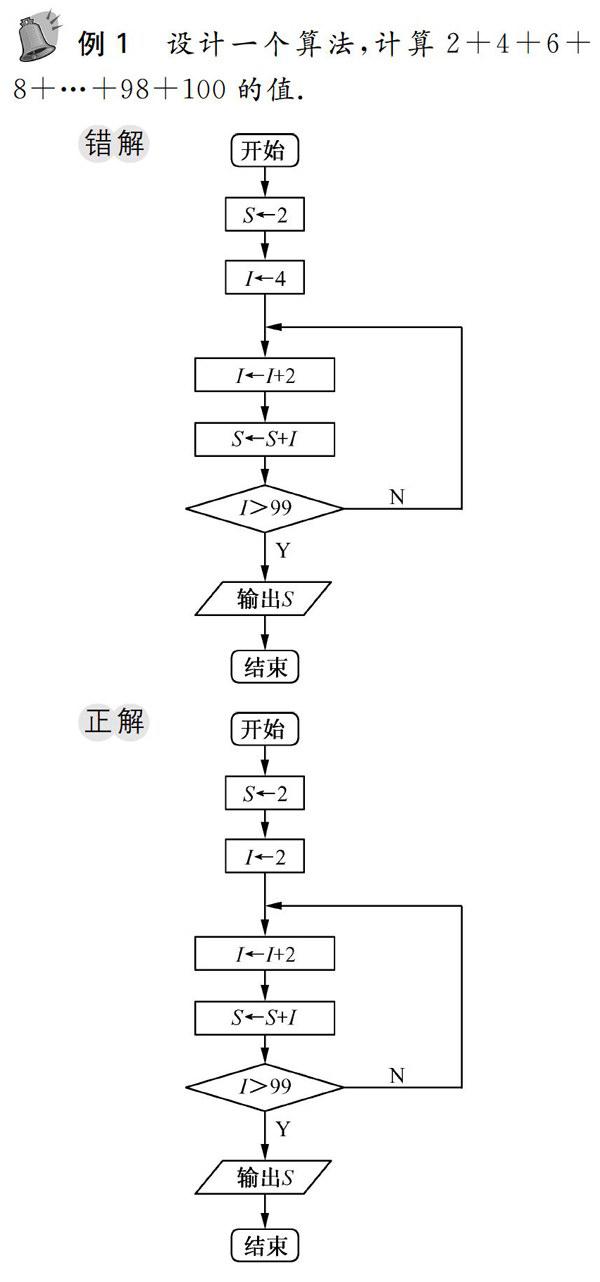
例1 设计一个算法，计算2+4+6+8+…+98+100的值.

剖析 这是一个直到型循环结构.有的同学只顾前两个值2和4，而不注意循环体执行带来的变化.按照前一个流程图执行出来的结果是2+6+8+…+100.错误的原因是I的初始值是4，而循环体中先执行了I=I+2，使得I的值变为了6，而致最终结果少加了4.简洁的修改可把初始值改为I=2即完成解答.

二、循环体内的执行先后有别

例2 设计一个算法，计算1×2×3×4×…×98×99的值.

剖析 这是一个当型循环结构.按照前一个流程图执行出来的结果是1×3×4×5×…×100.错因是循环体中按照箭头方向先执行了I=I+l，使得I的值变为了3，再执行T=T×I，而致最终结果少乘了2，多乘了100.把T=T×I与I=I+l的顺序颠倒一下即可得到正确的算法，算法是对一类问题机械的、统一的解决方法，其步骤的顺序不可随意颠倒.

三、判断条件要首尾兼顾

例3 写出一个计算10个数的平均数的伪代码.

分析 先利用循环结构计算10个数的和S，再计算10个数的平均数.句，先判断后执行.当I=l时，累加输入的第1个数，当I=2时，累加输入的第2个数，当I=3时，累加输入的第3个数……以此类推，当I=9时，累加输入的第9个数的和，而当I=10时，却不符合判断的条件而结束循环，即第10个数没有算人S，出错！简洁的修改方式可把I<10改为I

四、循环体内的赋值需各司其职

例4 写出一个计算1/1×3+1/3×5+1/5×7+…+1/99×101而的伪代码.

剖析 这是直到型结构的Do循环语句.同学们常因对变量S和变量I的认识不清，导致两者的赋值颠倒，从而出现与所求问题相差很大的结果，一般在循环结构中有两个变量，一个是变量S，用来贮存累加或累乘的结果；另一个是变量I，用来控制循环的次数和在S的基础上构建累加或累乘的变量形式，

在高考当中，命题者常常以循环结构为载体考查算法的相关内容.作为初学者，我们要认清循环结构的各种表达方式，比如直到型循环和当型循环，While语句和Do语句，理解它的每一个环节，把握算法是对一类问题机械的、统一的解决方法这一核心观念，按部就班地检验它的初值、判断条件、循环体及终点值，逐步调整，这样我们才能够以不变应万变，不被循环转昏了头！