讲究“思维”的算法

秉正

什么是算法？怎样书写算法？怎样进行“算法”的思维？

在中学阶段，这三个问题哪个才是学习算法的精髓？哪个更应该受到我们的重视？我以为是能形成“算法思维”，

何为算法思维？一句话，将解决问题的方法整理成算法的过程，是一个条理化、精确化和逻辑化的过程.怎样理解这句话的含义？怎样练就这样的思维呢？

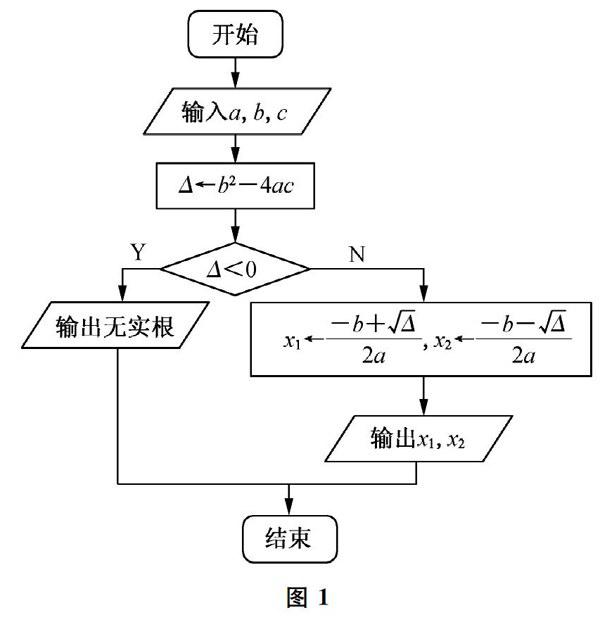
我们先来看一道课本上的例子，

流程图如图1.

解一元二次方程是我们熟悉的问题，解决问题的方法也已经在我们心中根深蒂固，事实上，本题给出的是一元二次方程的一般解法，只不过是用算法的角度进行了表达.这里把“解法”转化为“算法”，就是一个条理化、精确化和逻辑化的过程，

一、选择结构与分类讨论思想

在高中數学的学习中，我们都接触过分类讨论的思想方法，它曾经给很多同学的解题带来困扰.如上例，我们还会再继续追问.

若去掉条件“一元二次”及“a≠0”，如何求解方程呢？

分析 此时分类讨论将分为两个层次，应先对a是否为0进行讨论，因为待求解的方程已经不确定是否是一元二次方程了，若a =0，还有可能b=0，若a≠0时，再完成一元二次方程的求解过程，我们必须用到嵌套式的选择结构.写出该算法如下.

Sl 输入a，b，c，

站在算法的角度，我们更加清晰地认识了如何进行分类讨论，更加深入地理解了分类讨论的数学思想，而之前学过的分段函数也正是这一思想的实例，特别是分类讨论的标准如何建立，一直困惑着我们，同学们应该多尝试、多练习.

二、循环结构与递推思想

数列的递推关系与循环结构相结合的问题很常见，其目的是使同学们体会其中的循环思想，提高逻辑思维能力.数列与循环结构结合的本质特征是将循环结构中循环变量的初值与数列的首项作对应，将循环体中的某些语句与数列递推公式相对应.

数列中的递推关系与算法中的循环结构简直是“天造地设”的黄金搭档，不仅是两大思想的完美撞击，也是高考中的常客，对锻炼逻辑思维能力有着重要的作用，同学们应当给予足够的重视.此类问题还有如下两种常见的形式.

例3 （1）执行下面的流程图（图3），则输出的S=___

（2）执行下面的流程图（图4），计算前100项的和，则判断框应填入的关于I的条件是____________________.

不再详解，第（1）题答案为5，第（2）题答案为I≥200或I>199.

从知识角度看，以上两题也是算法与函数、算法与数列完美结合的实证，随着研究的深入，我们日渐拓展算法与其他知识的结合，近年来高考中陆续出现了算法与不等式、三角函数、概率统计相结合的题型，以算法为载体的创新题在高考试题中不断涌现，算法甚至像向量一样起到了工具性的作用，算法的思想也显得越来越重要，这将值得我们去研究和思考.