两个相同部件并联可修系统解研究
2018-11-22周莉
周 莉
( 齐齐哈尔大学 理学院, 黑龙江 齐齐哈尔 161006 )
0 引 言
两相同部件并联系统模型是可修系统模型的一种,是一种可靠性数学模型.可修系统模型包含串联和并联系统,允许对失效部件进行修理,修理后的部件可继续执行其使命,使其恢复功能.在实际生产生活中,为了改善系统的可靠性,经常采用维修的手段.由于引入了修理,模型的分析更加复杂.例如Huang等研究了多态连续n中取k可修模型[1-4],补充和深化了可修系统理论.而并联系统是包含多个部件,且有一个能够正常工作的完好系统,是具有较强的实用价值的可修系统.王定江[5]讨论了两相同部件并联可修系统的稳定性并应用强连续算子半群理论证明了系统非负解的唯一存在性;史定华[6]在∂p1(x,t)/∂t=0条件下用Laplace变换给出了解的Laplace变换公式,即得到了解的存在性.文献[7]中用C0半群理论研究了这个系统存在唯一非负的时间依赖解.郭卫华[8]用迭代法证明了该系统非负解的存在性和唯一性.本文在两相同部件并联系统中用初等阶梯函数对其修复率进行逼近,用半离散算法[9-10]将该系统转化为两个离散化数学模型,并且运用泛函分析理论证明系统模型动态解的逼近.
1 数学模型
一类两个相同部件并联可修系统的模型见图1.

图1 两个相同部件并联可修系统的模型
该模型可用积分-微分方程组(系统Ⅰ)描述为
(1)
(2)
p1(0,t)=λ(k+1)p0(t)
(3)
p0(0)=1,p1(x,0)=0
(4)
式中:p0(t)表示在时刻t两个部件完好的概率;p1(x,t)dx表示在时刻t一个部件完好另一个部件故障并且故障的部件在(x,x+dx]内被修好的概率;λ表示部件的平均寿命;μ(x)表示部件的修复率,满足
0≤μ(x)<∞

k表示正比失效率,k=1时表示并联,0
2 泛函分析处理
下面在Banach空间中用抽象Cauchy问题的形式来描述这个系统.
设算子
取状态空间
显然,X是Banach空间.算子A的定义域为

则式(1)~(4)可以描述成Banach空间X中一个抽象的Cauchy问题.
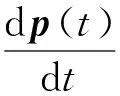
(5)
p(0)=(1 0)T
(6)
3 计算模型半离散化
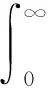
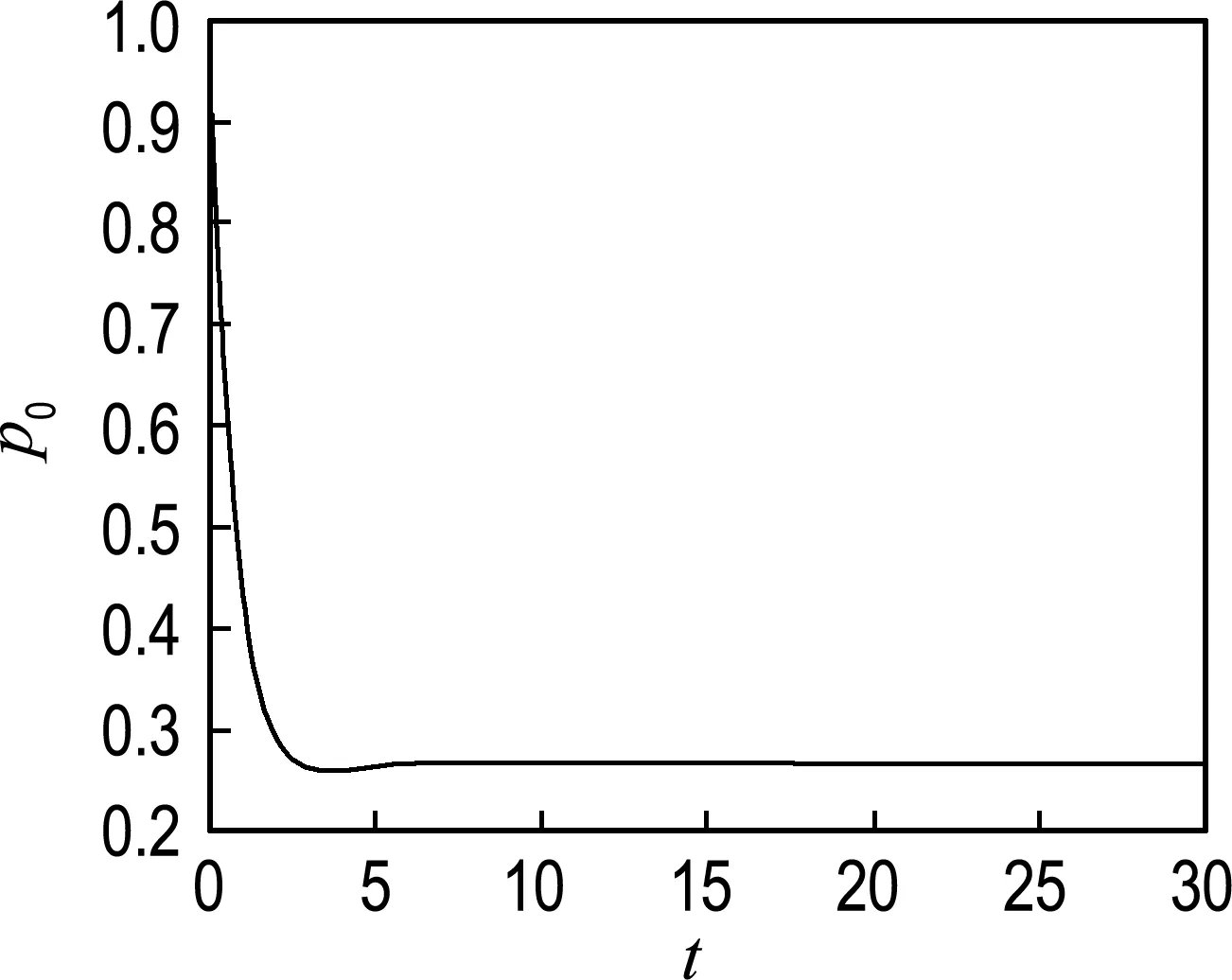
0=a0 令 Δi=[ai-1,ai],x0∈(0,∞) 下面构造阶梯函数: 则由假设,对任意的ε>0,存在x0∈[0,∞)使得 |μ(x)-μ*|<ε 与 |μn(x)-μ(x)|<ε 进而原模型经离散后化为式(1)′~(4)′(即原系统的修复率μ(x)置换为μn(x)),则原偏微分方程变为常微分方程系统(1)′~(4)′,如同前面一样把式(1)′~(4)′用Banach空间中的抽象Cauchy问题来描述: (7) pn(0)=(1 0)T (8) 由线性算子半群对偏微分方程的应用及文献[11]知:A+B生成一个C0压缩半群,又因为生成C0半群具有唯一性,所以此压缩C0半群就是T(t). 首先估计线性算子A+B和(An+Bn)的预解式分别为R(v;A+B)和R(v;An+Bn),然后对系统动态解的逼近问题用Trotter定理加以证明. 考虑方程[vI-(A+B)]p(x)=y(x),即 (9) (10) p1(0)=λ(k+1)p0 (11) 由式(11)可得 (12) 令 将式(12)代入式(9)得 (13) 令 整理得 (v+λ(k+1)(1-ω))p0=y0+φ(y1) (14) 令 |D|=v+λ(k+1)(1-ω)= 所以由文献[12]得出当v>0时|D|≠0方程(14)的解是唯一的,因此方程组(9)~(11)的解也是唯一的,进而有R(vI-A-B)X,(vI-A-B)是闭算子,且(vI-A-B)-1也存在并且是有界的.而|D|能用ω线性表示,所以当v>0时 (exp(-vx)为减函数)= 即0<|ω|<1,那么|D|也是有界的.所以由式(14)得 将p0代入p1(x)则有 取 因此A+B的预解式为 将(vI-A-B)-1中ω、φ(y1)、W、Q(y1)、|D|含有的μ(x)变为μn(x)得到(vI-An-Bn)-1,相应的ω、φ(y1)、W、Q(y1)、|D|记为ωn、φn(y1)、Wn、Qn(y1)、|Dn|,Λ记为Λn,于是得到 现在来证明系统修复率的逼近,只要证明R(v;An+Bn)y→R(v;A+B)y. 只需证明 且|Dn||D|≠0,|Dn|、|D|有界(n→∞).|D|≠0同理|Dn|≠0,且|Dn|有界,|D|为ω的线性表示,ω中含有μ(x),要证明|Dn|→|D|,只需证明ωn→ω(n→∞). 考虑 则有|ωn|→|ω|(n→∞),即|Dn|→|D|(n→∞). 证明Λn→Λ(n→∞),只需证明相应元素逼近,即 φ(yn)→φ(y1),Wn→W, Q(yn)→Q(y1)(n→∞) μ(ξ)|dξ→0 (n→∞) 0 (n→∞) |μn(x)-μ(x)|· μ(x)|dξdτdx→0 (n→∞) 综上所述 |Λn|→|Λ| (n→∞) 亦即 即 R(v;An+Bn)y→R(v;A+B)y(n→∞) 这样就证明了系统动态解的逼近. 为了验证以上离散后的常微分方程组解的收敛性,用实践证明理论的正确性.下面利用数值计算方法[13],对上述结果进行数值模拟. (15) (16) p0(0)=1,p1(0)=0 (17) 下面用Matlab数学软件求常微分方程组的数值解,此时令λ=0.5,μ=0.5,其结果如图2所示. 对图2进行分析表明本文建立的离散化模型具有系统动态解.这个结论与理论证明的结论是一致的,进而说明半离散算法对于该可修系统模型是可行的. (a) p0 (b)p1 图2 系统(Ⅱ)的数值解(μ(x)=μ,为常数) Fig.2 Numerical solution of system (Ⅱ) (μ(x)=μ,is constant) 理论分析表明半离散化逼近方程能够保持许多原来重要问题的物理意义,所以该逼近方程就可以作为原物理问题的常微分方程模型[14-15].本文利用半离散化方法将两相同部件并联可修系统模型转化为矩阵常微分方程组,证明了该方程组解是收敛的.当假设修复率为常数时对模型解进行数值分析与计算,得到该模型的拟合图.4 动态解逼近的证明


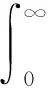


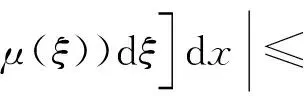


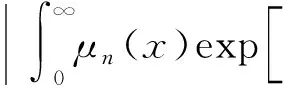












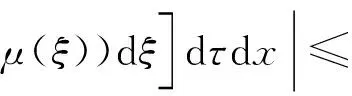





5 数值计算模型
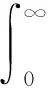



6 结 语
