优雅图猜想

赵 科， 李 敬 文， 魏 众 德

( 兰州交通大学 电子与信息工程学院， 甘肃 兰州 730070 )

0 引 言

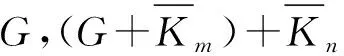
国内外学者主要在研究特殊图的优雅性，例如圈、路、扇图等目前已经证明是优雅的．Rosa提出非优美图产生的3个原因[8]：(1)图G的顶点过多而边数太少；(2)图G边数过多而顶点太少；(3)图G的边数具有错误的奇偶性．以上条件同样适用于优雅标号．本文根据文献[9]中生成非同构图的算法，得到9个点之内的所有连通图，结合设计的优雅标号算法，得到所有优雅图和非优雅图的数量．

1 定义及基本概念

定义1[1]对于任意的简单连通图G=(V，E)，如果对每一个顶点v∈V，都对应一个非负整数f(v)(f(v)为顶点v的标号)，且满足

(1)∀v1，v2∈V，如果v1≠v2，则f(v1)≠f(v2)；

(2){f(v)|v∈V}∈{0，1，2，…，|E|}；

(3)∀e1，e2∈E，如果e1≠e2，则g(e1)≠g(e2)，其中g(e)=(f(v1)+f(v2))mod (q+1)，e=v1v2；

(4){g(e)|e∈E}∈{1，2，…，|E|}

则称f为图G的一个优雅标号，图G称为优雅图．

定义2对于边数为q的优雅图，满足以下条件：

(1)min(f(u)，f(v))≥0；

(2)max(f(u)，f(v))≤|E|；

(3)(f(u)+f(v))mod (q+1)=g(e)，且g(e)≠0

则称为边数为q的优雅集合，又称q优雅空间．如表1所示，对于每个g(e)，只取一个二元组(m，n)，这些二元组集合组成的图都是优雅的．

m的取值范围为{0，1，…，q}；n的取值范围可通过如下公式：n=g(e)-m≥0？g(e)-m：g(e)-m+q+1判断取得．

在优雅空间中，当m=n时，因每个点的标号不同，故去除；为了避免重复，当m>n时，去除该二元组(m，n)．具体如表1所示．

表2为(5，10)图的优雅空间，其中粗体的二元组为它的一种优雅标号，如图1所示．

表1 q优雅空间

表2 q=10优雅空间

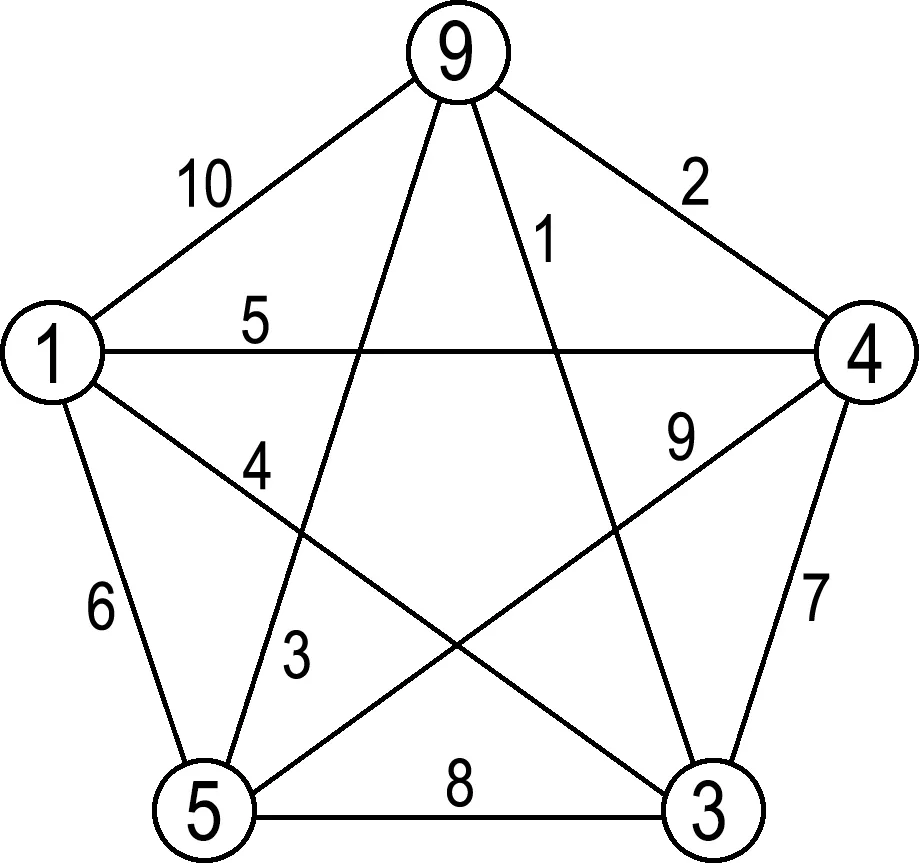
图1 (5，10)图优雅标号

猜想1[1]所有的树都是优雅的．

2 解决思路及算法

2.1 解决思路

本文所研究的图均为简单连通图，具有p个顶点和q条边的图称为(p，q)图，其中q的范围为p-1≤q≤p(p-1)/2．当p-1>q时，该图为非连通图，不在本文研究范围之内．判断任意一个连通图是否为优雅图的解决思路如下：

(1)根据(p，q)图的边数q生成图的优雅空间，可组合成的图G如下：

(2)G个图都是优雅图，由连通图与非连通图组成；

(3)任意一个连通图若是优雅图，则一定在图G中；若不在其中，则该图一定为非优雅图．

2.2 设计的优雅图判定算法

算法的基本思想是：对于给定的任意一个连通图，可以用矩阵形式将它表示，记为M(n，n)，其中n表示顶点个数，若顶点i与顶点j之间有边，则Mij=1(i≠j)，若无边Mij=0(i≠j)．标号过程为根据该图的边q生成优雅空间，先根据预判函数判断q=1时的二元组(i，j)是否可用，若可用将相邻的顶点标号，将两个顶点对应的边标为1，边数以1递增，直到边为q+1时标注成功．在选择二元组过程中，若二元组(i，j)不可用，则寻找下一个二元组．

具体算法步骤如下：

Input：一个图的邻接矩阵M(n，n)

Output：该图是否为优雅图

1.Begin：

2.Calculate the number of edges， generate an Elegant space；

3.edgeCount∈{1，2，…，q，q+1} SetedgeCount=1；

4.DeepSearch(edgeCount)

5.{

6. If (edgeCount=q+1)

7. Success and quit；

8. Select a two tuple (p1，p2)；

9. Forp10→q

10.p2=edgeCount-p1>=0?edgeCount-p1：edgeCount-p1+q+1；

11.edgeCount=(p1+p2)%(q+1)

12. Checkp1andp2in Matrix；

13. Fori1→n

14. If (Miican be used)Mii=p1；

15. Forj1→nandi≠j

16. If (Mjjcan be used &&Mij==1)

17. {

18.Mjj=p2；

19.Mij=edgeCount；

20.edgeCount=edgeCount+1；

21. DeepSearch(edgeCount)；

22. }

23. End Forj1→nandi≠j

24. End Fori1→n

25.}

26.If (Elegant space is Finished)

27. This Graph is UnElegant；

28.End

3 算法结果与分析

本文根据文献[9]提供的算法，生成9个点之内的所有非同构图，用邻接矩阵的形式将其保存到p_q.txt文件中．运用本文设计的任意图的优雅判断算法，对所有图进行验证，列表统计了9个点内所有优雅图和非优雅图的数目，并对比了各点对应的图中非优雅图所占比率．

3.1 点数为2～9的所有图优雅图个数统计

当q=p-1时，图为树图；当q=p(p-1)/2时，图为完全图．即对于所有的连通图，其边数q的取值范围为p-1≤q≤p(p-1)/2．

程序结果表明，当p=2时，图的个数为1，且为优雅图；当p=3，q=2，3时，图的个数为2，且都是优雅图，为简洁不再列表说明．对点数4～9的所有图列表给出，其中N(UG)为非优雅图个数，N(EG)为优雅图个数，N(G)为图的总数，见表3～8．

由表3～8可以看出，(4，3)、(6，5)、(8，7)图为树图，其中至少有一个非优雅树图，即图G有太多的顶点且没有足够的边会导致产生非优雅图；(6，14-15)、(7，20-21)、(8，25-28)、(9，31-36)图都是稠密图，且都是非优雅图，即图G有太多的边且没有足够多的顶点会导致产生非优雅图；(4，4-6)、(5，5-10)、(6，6-13)、(7，7-15)、(8，8-17)、(9，9-21)图中，当边q=1(mod 4)时，存在非优雅图，且所占比例逐渐递增，而当q≠1(mod 4)时，所有图都是优雅图，即图G的边数具有错误的奇偶性会产生非优雅图．

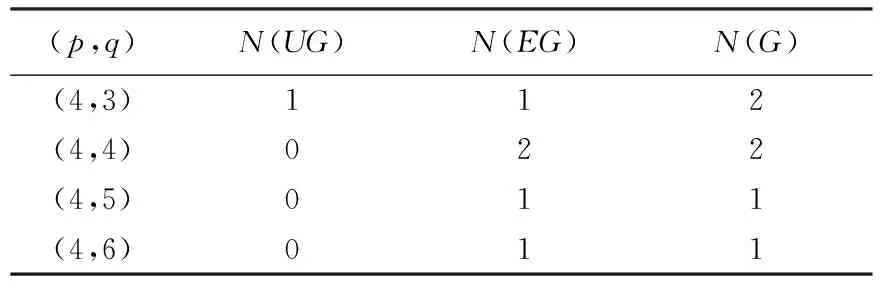
表3 点数为4的图

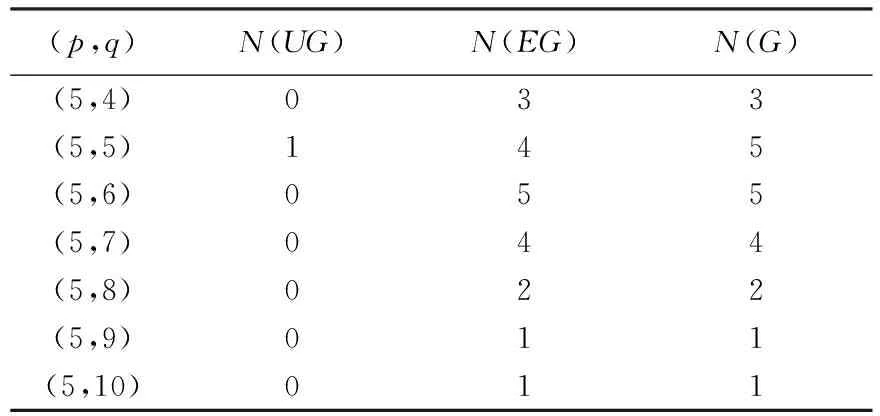
表4 点数为5的图

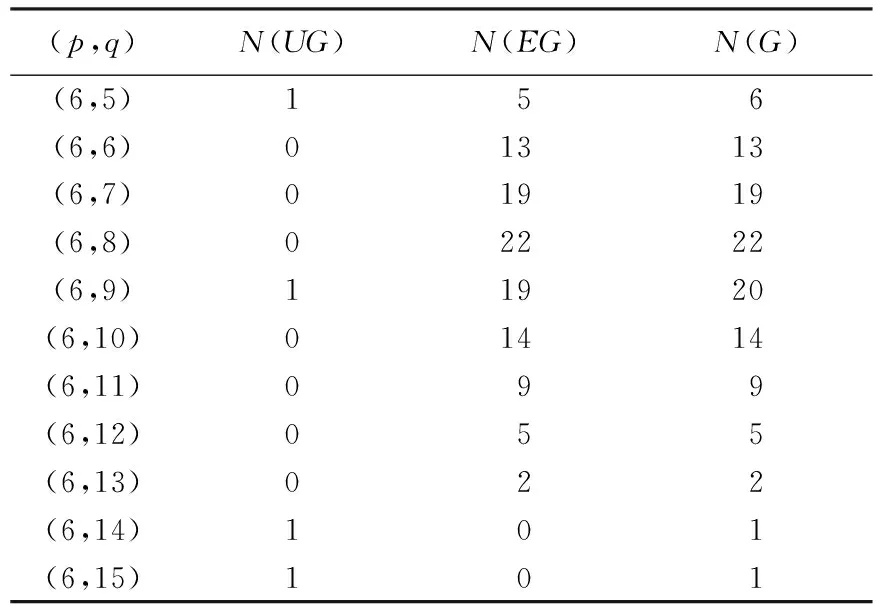
表5 点数为6的图

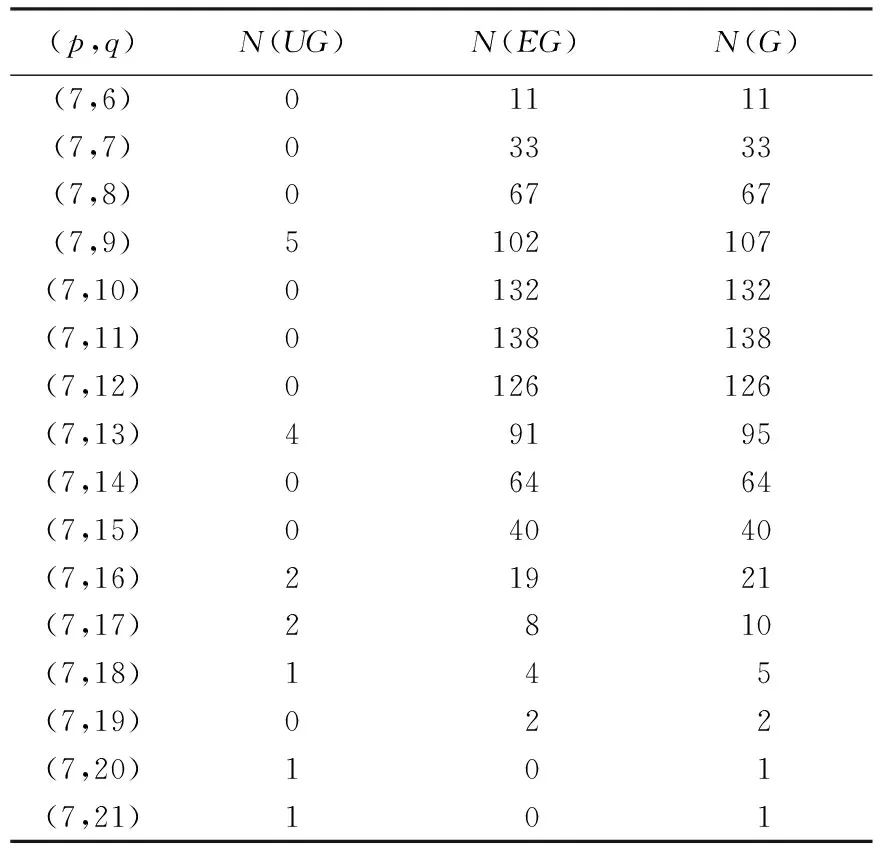
表6 点数为7的图

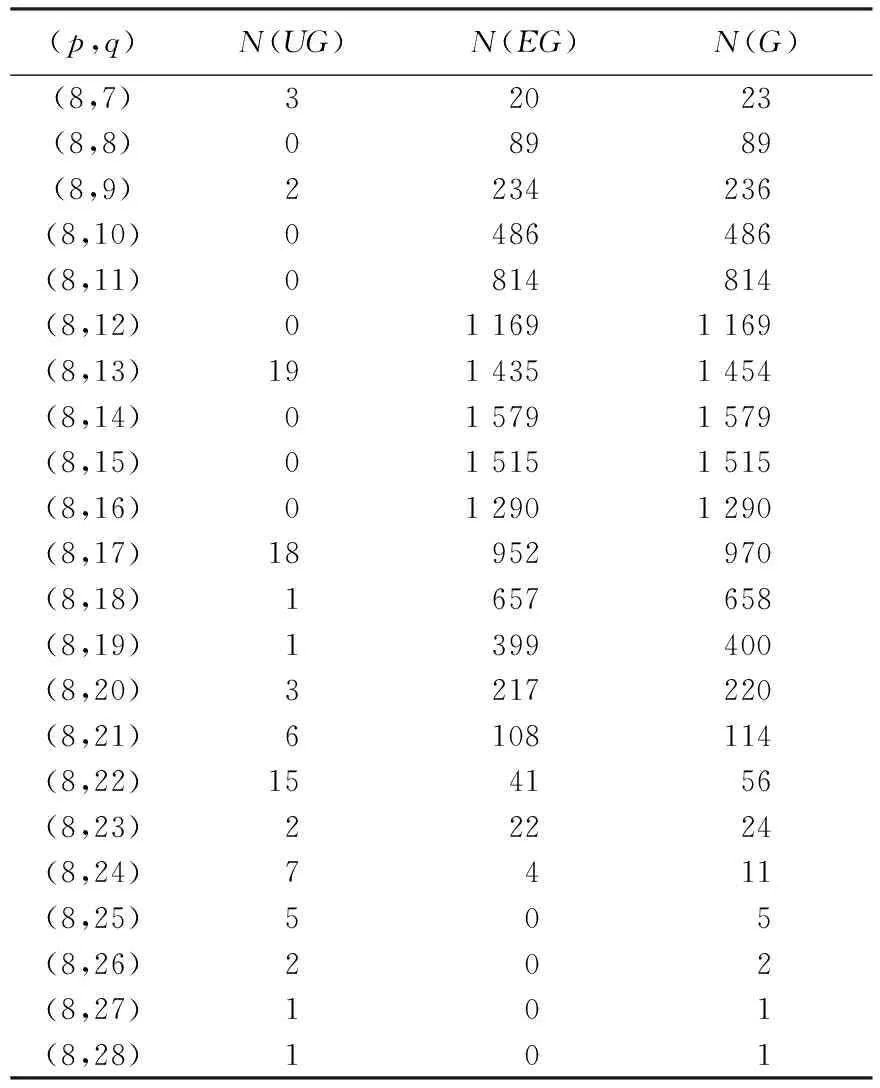
表7 点数为8的图

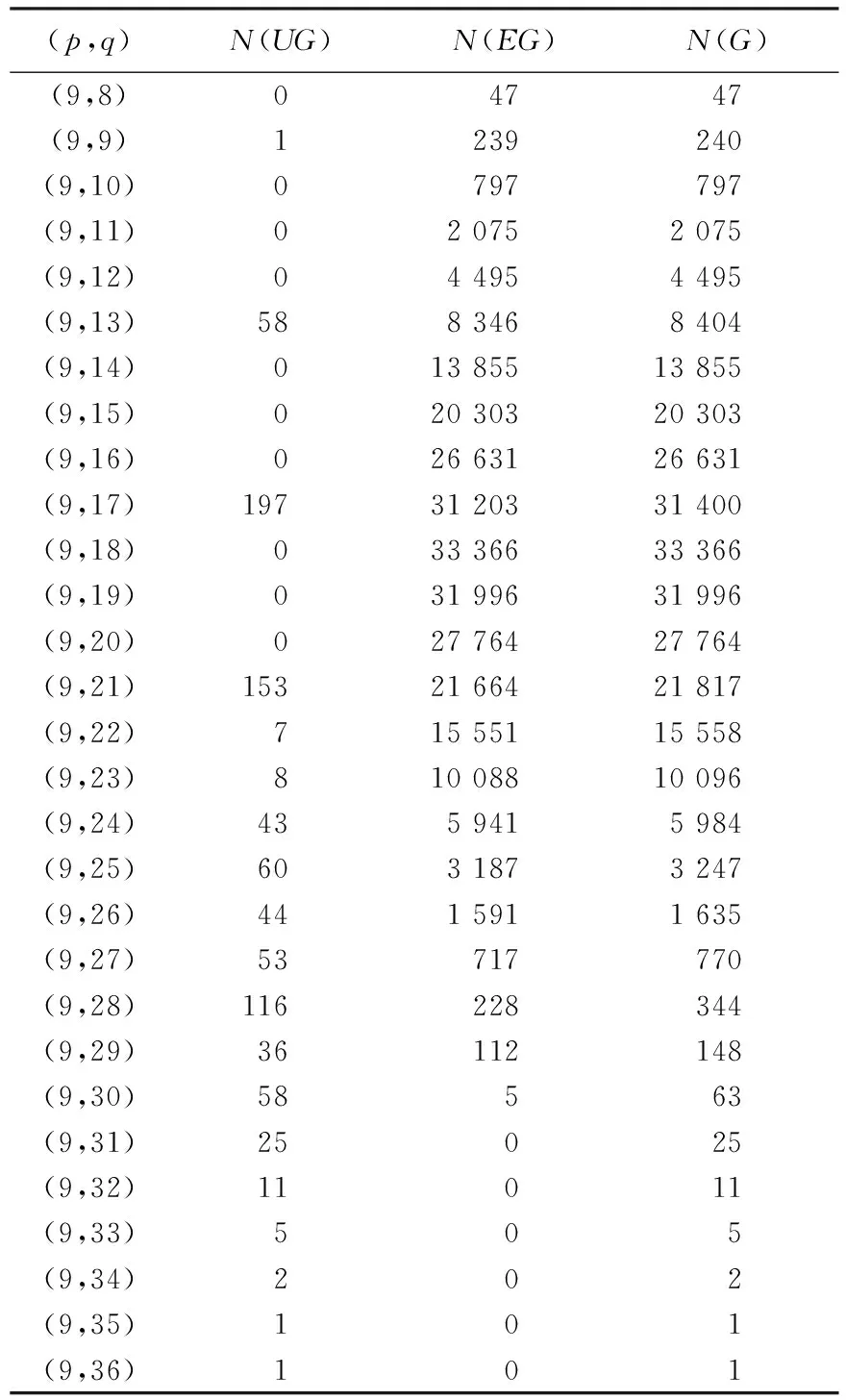
表8 点数为9的图

3.2 定理和猜想

根据上述实验结果，得到以下结论：

定理1当3≤p≤9时，树T(p，q)几乎都是优雅的，其中

证明(1)当p为奇数时，所有的树T(p，q)的优雅性如表9所示．由表可知，所有的奇树T(p，q) 都是优雅的．

(2)当p为偶数时，树T(p，q)的优雅性如表10所示．由表可知，随着点数的增加，非优雅树的比率递减．

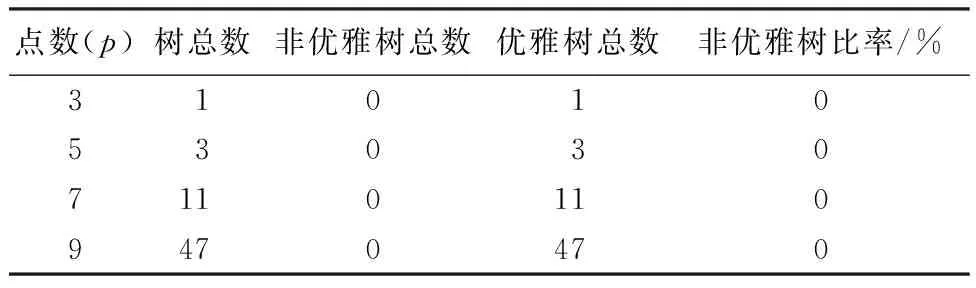
表9 3～9个点内所有奇树的非优雅数对比

表10 3～9个点内所有偶树的非优雅数对比

综合(1)、(2)可知，当3≤p≤9时，树T(p，q)几乎都是优雅的．

定理2当3≤p≤9时，除了图C5、C9外，所有的单圈图都是优雅的．

证明9个点以内的单圈图由表3～8得出．

猜想2当q≠1(mod 4)时，所有的单圈图是优雅的．

定理3当2≤p≤9，p≤q≤2p且q≠1(mod 4)时，所有(p，q)图都是优雅的．

证明由表3～8可知，当q=p-1时，所有的图都是树图，满足定理1．当p≤q≤2p且q≠1(mod 4)时，所有(p，q)图都是优雅图．而q=1(mod 4)时，其中部分图是非优雅的．由此可知，图的优雅性与图的边数存在一定的相关性．

猜想3当p-1≤q≤2p且q≠1(mod 4)时，所有图都是优雅的．

虽然非优雅图较多，但在图的总数中占比极小，如表11所示．除顶点p=2，3之外，随着顶点数的增加，非优雅图占比越来越小，从而提出猜想4．

表11 2～9个点内所有图的优雅数对比

猜想4所有图几乎都是优雅图．

3.3 9个点之内的部分非优雅图

虽然9个点以内的所有非优雅图数量占总图数的比例较低，但数量依然较大，只选取其中比较特殊及常见的部分非优雅图，命名方式为p_q_number，其中number表示为(p，q)图中列举的非优雅图顺序，若只有一个非优雅图，则number予以省略．

点数为4的非优雅图已经由文献[2]给出，共有1个，如图2(a)所示．

点数为5的非优雅图有1个，由文献[1]给出，并证明了圈图Cn的优雅性，如图2(b)所示．

(a)p=4

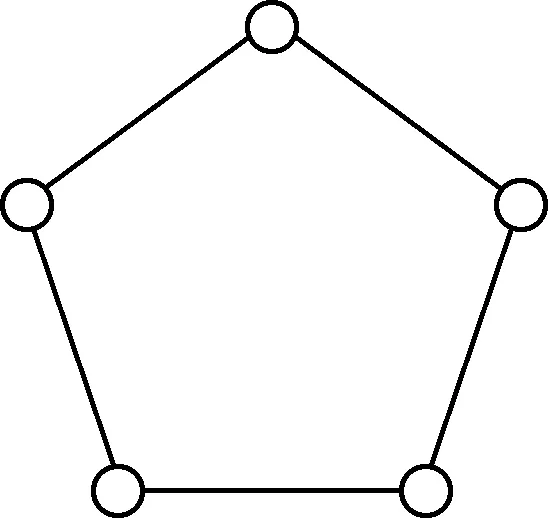
(b)p=5

图2p=4，5的非优雅图

Fig.2 Non-elegant graph whenpis equal to 4, 5

点数为6的非优雅图共4个，如图3所示．点数为7的非优雅图共16个，部分如图4所示．

图3 p=6的非优雅图

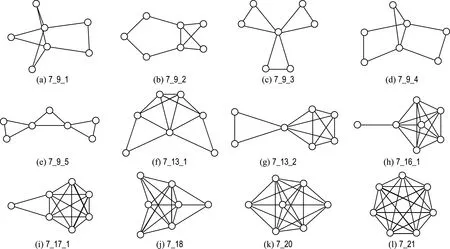
图4 p=7的部分非优雅图

点数为8的非优雅图共86个，部分如图5所示．点数为9的部分非优雅图如图6所示．

3.4 9个点内部分优雅图

为了证明本文提出算法的可行性及有效性，随机选取了部分优雅图，其顶点数及边数都较大，在不借助计算机程序的条件下，传统人力标注较难完成．(8，19)、(8，23)、(9，14)、(9，18)、(9，20)、(9，29)图部分优雅图如图7、8所示．

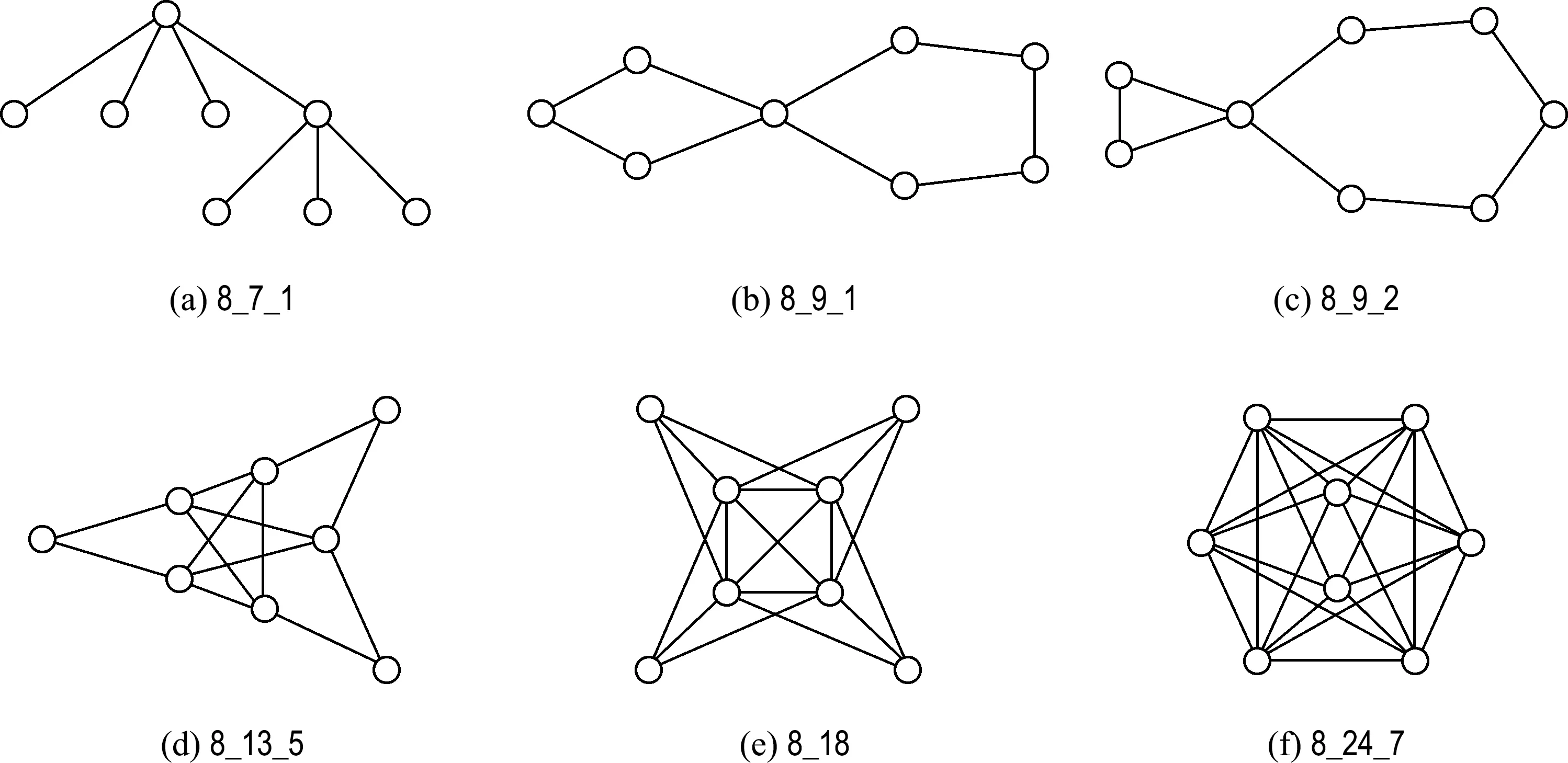
图5 p=8的部分非优雅图

图7 p=8的部分优雅图

图8 p=9的部分优雅图

4 结 语

图的标号问题由来已久，传统的研究方式往往局限于小点数图形及某类特殊图，通过对小点数的图形进行标号，观察其中的规律，然后拓展去验证大点数的该类型图，但这种方式具有局限性，且效率低下，无法完成对9个点内的所有图进行标号，因而无法发现优雅标号的普遍规律．本文通过程序设计，提出了深度遍历搜索优雅空间的思想，可以搜索出该图的所有优雅标号．本文完成了9个点之内所有图的优雅性判断，提出了定理和猜想并给出相关数据及部分非优雅图，为图标号领域内进一步证明相关猜想提供了基础数据支持．

通过对程序的结果进行分析，对一个图G是否优雅做如下判断：(1)所有的奇树都是优雅的；所有的偶树中至少有一棵非优雅树，但大多数偶树都是优雅的．(2)当p-1≤q≤2p且q≠1(mod 4)时，所有图都是优雅的．

研究可知，2～9个点内图的总数为273 192，优雅图为272 205，优雅比率达到99.638 7%；针对研究中的发现，本文提出一个公开问题如下：当q≥2p时，这类(p，q)图全部是优雅的，如(9，19)图中31 996个图、(9，20)图中27 764个图全部是优雅的，这类图具有怎样的特性？该如何刻画？