基于修正压力场理论的活性粉末混凝土梁抗剪分析
2018-11-22王强,金凌志*,蒋春松
王 强, 金 凌 志*, 蒋 春 松
( 1.桂林理工大学 土木与建筑工程学院, 广西 桂林 541004;2.桂林理工大学 广西岩土力学与工程重点实验室, 广西 桂林 541004 )
0 引 言
普通的钢筋混凝土梁的抗剪问题十分复杂,国内外规范中的抗剪承载力计算方法大多为半理论半经验公式,力学模型不明确,基本以试验数据回归得到.且出于对工程安全的考虑,其计算结果一般都比较保守.20世纪初Ritter与Mörsch提出了经典45°桁架模型,以力学为基础的计算方法逐渐得到认可,并不断发展完善,其中以20世纪80年代加拿大学者Vecchio和Collins[1-2]提出的修正压力场理论(MCFT)较为经典,并成为《加拿大桥梁结构设计规范》[3]、《加拿大混凝土结构设计规范》[4]和《美国桥梁结构设计规范》[5]中抗剪计算方法的理论基础.该理论忽略纵筋的消栓作用,将裂后混凝土仍看成连续性材料,应力和应变都取平均值,同时满足莫尔圆定理.依据混凝土和钢筋微元体单元在整个受荷过程都需满足假定的本构关系、相容方程和应力平衡条件,考虑裂缝间混凝土骨料的咬合力和摩擦力,给出钢筋混凝土构件在纯剪作用下的模型公式,若叠加弯矩作用,则可得到其在弯剪共同作用下的计算模型[6-7].该模型未忽略开裂后混凝土的拉应力,故钢筋混凝土构件的非线性性能即全阶段荷载-变形特征能被准确描述.
活性粉末混凝土(reactive powder concrete,RPC)是法国Bouygues试验室在20世纪90年代研制出的一种具有超高强度、高韧性、高耐久性的新型水泥基复合材料[8],且在材料特性方面已有较多研究[9-11].2015年《活性粉末混凝土》(GB/T 31387—2015)[12]颁布,对RPC各组分的配合比、制备技术、养护条件、强度等级的划分与测试方法等进行了统一规定,标志着RPC工程应用时代的到来,所以相关结构设计规范也理应被提上日程.RPC的强度较高,若受力纵筋仍采用现行工程中主推的HRB400级钢筋,对于非预应力构件则会出现配筋率过高的情况,对施工造成不便,故用高强度钢筋与RPC组成的结构构件近年来受到更多的关注[13-14].鉴于此,本文采用的主受力筋为HRB500级钢筋.
文献表明[15-17],配筋RPC构件的研究主要以试验为主,而相应深入的理论模型分析较少.本文在Vecchio和Collins提出的MCFT(混凝土板受纯剪)基础上,叠加弯矩效应,结合RPC材料特点,建立在弯剪复合作用下配筋RPC梁截面受荷全过程分析模型,并将分析结果与试验结果进行对比.
1 模型的建立
1.1 平衡方程和相容条件
(1)基本假定
如图1所示,平面钢筋单元和RPC单元共同承担开裂钢筋RPC单元的外力,假定钢筋只能承担拉力和压力,忽略其抗剪作用,则
fx=fcx+ρsxfsx
(1)
fy=fcy+ρsyfsy
(2)
vsxy=0
(3)
vxy=vcxy+vsxy=vcxy=v
(4)
式中:ρsx和ρsy分别为钢筋单元x向和y向配筋率;fcx和fcy分别为RPC单元x向和y向正应力;fsx和fsy分别为钢筋单元x向和y向正应力;fx和fy分别为钢筋RPC单元x向和y向正应力;vxy、vcxy和vsxy分别为钢筋RPC单元、RPC单元和钢筋单元的剪应力.
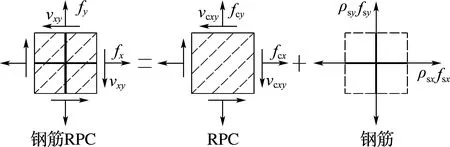
图1 钢筋RPC平面应力单元
(2)相容方程(开裂钢筋RPC单元)
如图2(a)所示,ε1和ε2分别为穿越几条斜裂缝的平均主拉应变和主压应变,裂缝倾角为θ,假定RPC和钢筋之间无滑移,即如图2(b)所示,单元整体应变符合莫尔圆理论,则
(5)
由三角形2Ax和2By的几何关系可得:
γxy=2(εx-ε2)cotθ
(6)
γxy=2(εy-ε2)tanθ
(7)
由式(5)~(7)可得:
(8)
(9)
式中:εx和εy分别为钢筋RPC单元x向和y向应变,γxy为其剪应变.
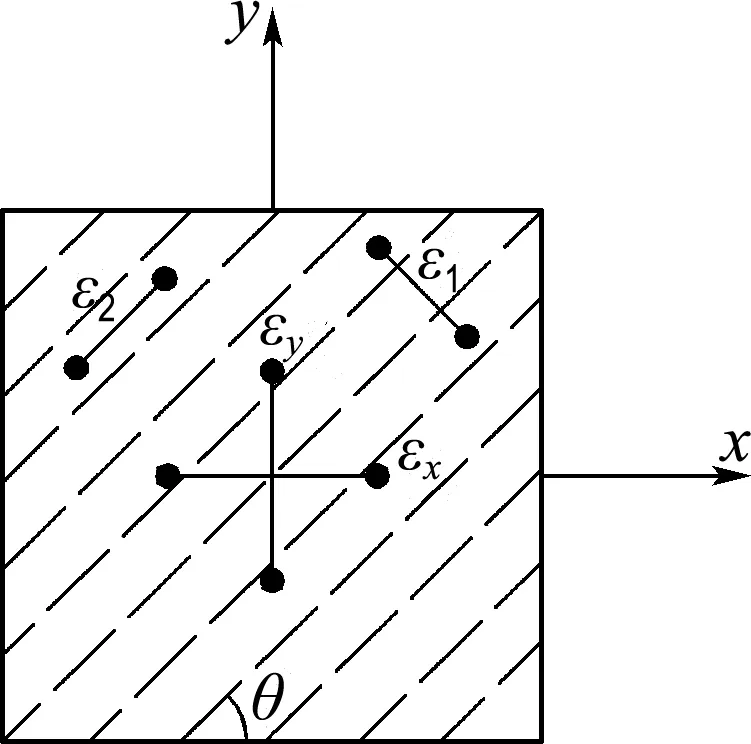
(a) 单元平均应变(开裂后)
(3)开裂RPC单元应力平衡条件
假定开裂后RPC单元主应变与主应力的倾角方向相同,大小均为θ,见图3,则
fc2=-fc1+v(tanθ+cotθ)
(10)
其中fc1和fc2分别为开裂后RPC单元的主拉应力和主压应力.
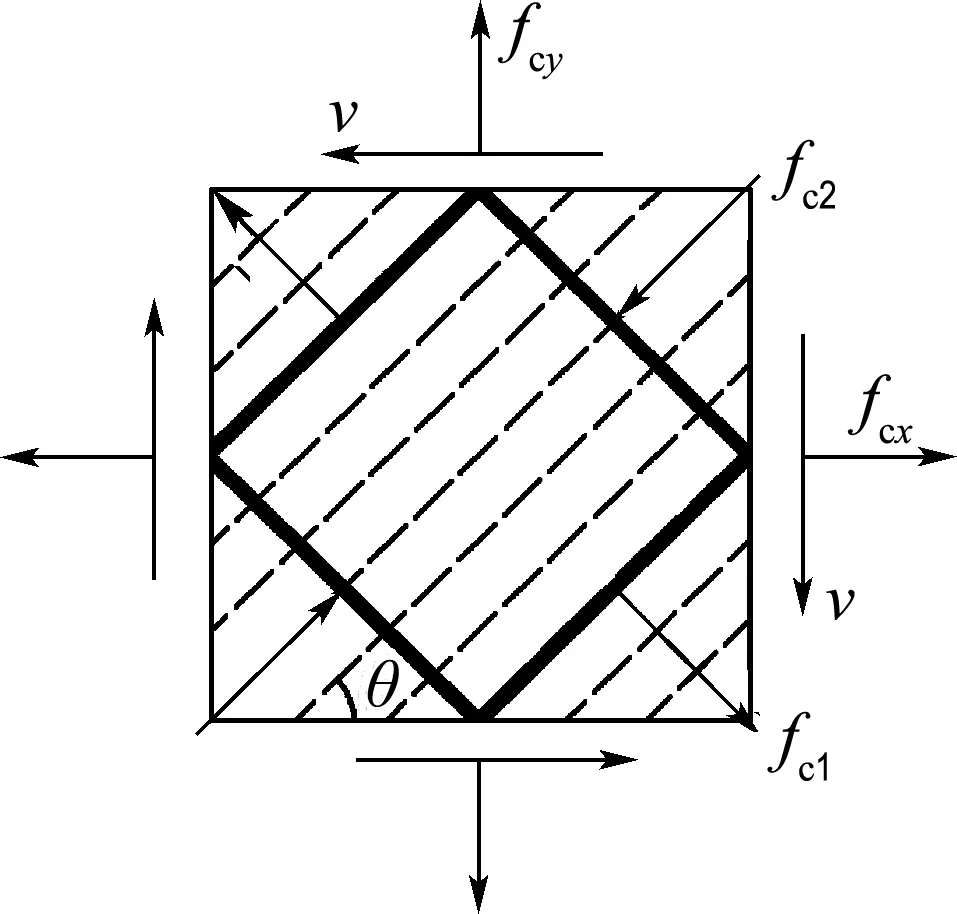
(a) RPC单元主应力(开裂后)
1.2 材料的应力应变关系
(1)钢筋
钢筋的本构关系采用双直线模型,即
当εs≤εyv时(上升段),有
fsy=εsEs
(11)
当εyv<εs≤εsu时(水平段),有
fsy=fyv
(12)
式中:εyv为箍筋的屈服应变,Es为钢筋的弹性模量,εsu为钢筋的极限拉应变,fyv为箍筋的屈服强度.
(2)RPC
①RPC受拉应力应变关系.文献[18]给出了RPC轴拉σ-ε曲线,但未给出具体模型,其形状与文献[19-20]中钢纤维混凝土材料的受拉本构模型(见图4(a))相似,故可近似采用,其公式为
当ε1≤εcr时(上升段),有
(13)
当ε1>εcr时(下降段),有
(14)
(15)
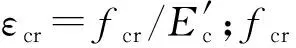
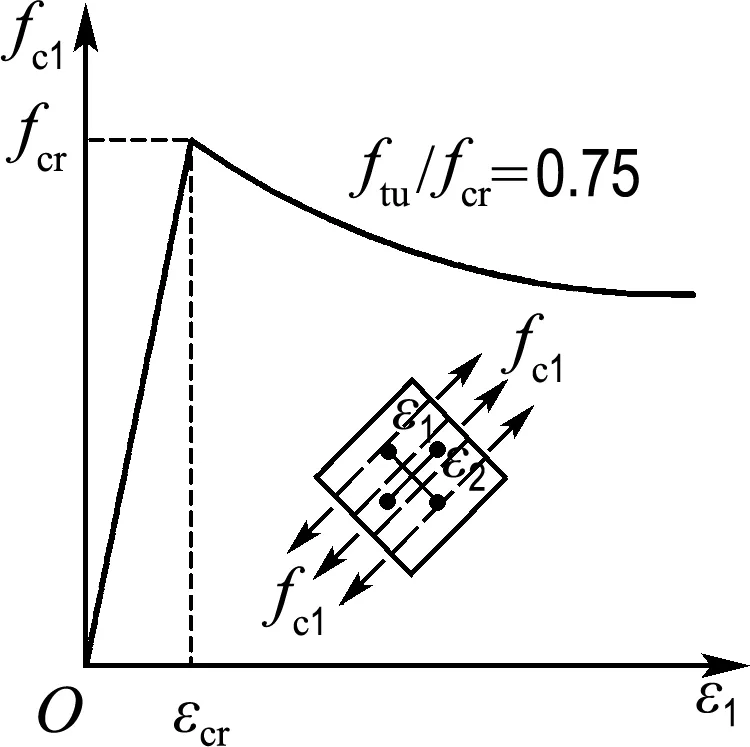
(a) 受拉本构关系
②RPC受压应力应变关系.普通混凝土材料在受到拉压二维应力共同作用时,其极限抗压强度比只受一维压应力时的极限抗压强度低的现象被称为软化现象,RPC也存在该现象.弯剪复合应力下的RPC单元也是处在拉压二维应力的共同作用下,故单元的主压应力不仅与主压应变有关,与主拉应变也有很大关系.为考虑RPC材料的软化现象,也可用文献[20]中钢纤维混凝土的受压本构模型来代替,如图4(b)所示,其公式为
(16)
(17)
1.3 梁在纯剪下的应力分析
(1)应力平衡(裂缝之间)
(18)
其中V为截面受到的剪力.由图5(c)箍筋方向力的平衡可得
fsyAsy=(fc2sin2θ-fc1cos2θ)bs
(19)
由式(10)、(18)、(19)可得
(20)
当RPC达到极限抗拉强度(fc1=ft)以及箍筋屈服(fsy=fyv)时,式(20)即为梁在纯剪下的承载力表达式.同时可求出梁在纯剪作用下所受剪力的水平分量Nv的表达式为
Nv=bdv(fc2cos2θ-fc1sin2θ)=Vcotθ-fc1bdv
(21)
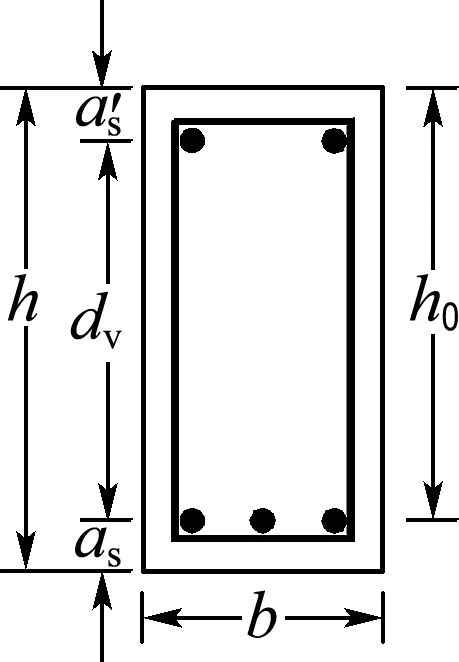
(a) 截面参数
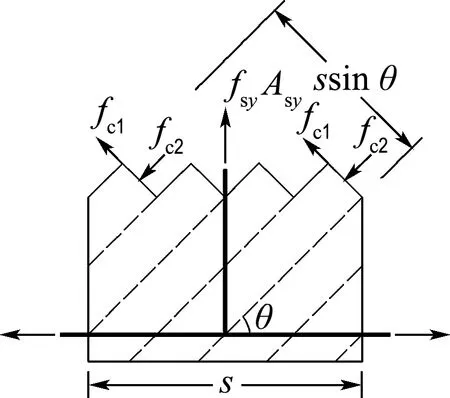
F(c) 箍筋的力
图5 纯剪下梁的应力
Fig.5 Stress of beams under pure shear
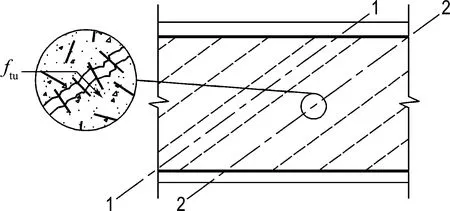
(2)跨越裂缝的力的平衡
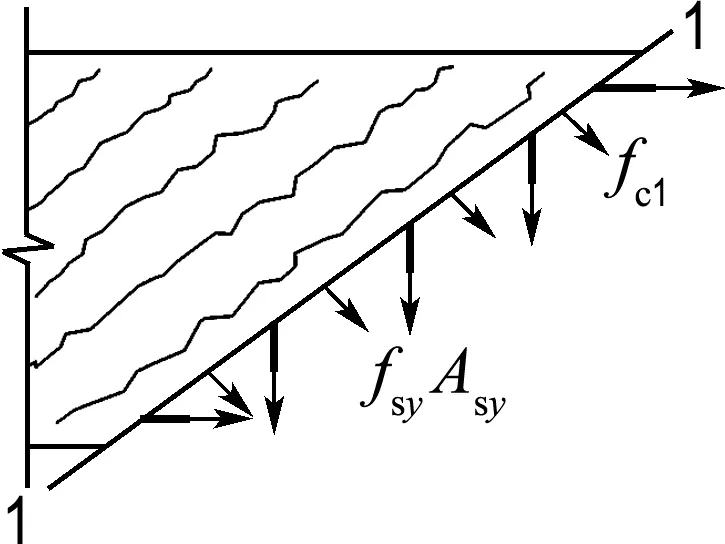
MCFT的基本假定将斜裂缝处混凝土面理想化为光滑平面,但实际情况是会存在裂缝处界面上的骨料咬合作用.RPC中虽无粗骨料,但含有钢纤维,所以开裂后界面上虽不存在骨料咬合力,但会出现钢纤维的抗拔阻力.且当外荷载较大,箍筋屈服后应力保持稳定时,RPC在裂缝处的拉应力已基本只剩余钢纤维的抗拔阻力,1-1截面(裂缝间)和2-2截面(裂缝处)两处的应力应相等,如图6所示,由竖向力的平衡可得
(22)
式中:fsycy为箍筋的拉应力,当fsycy=fyv,即箍筋屈服时,fc1达到极限值fc1max,则
(23)
(a) 裂缝处钢纤维的抗拔阻力
(b) 裂缝间平均应力
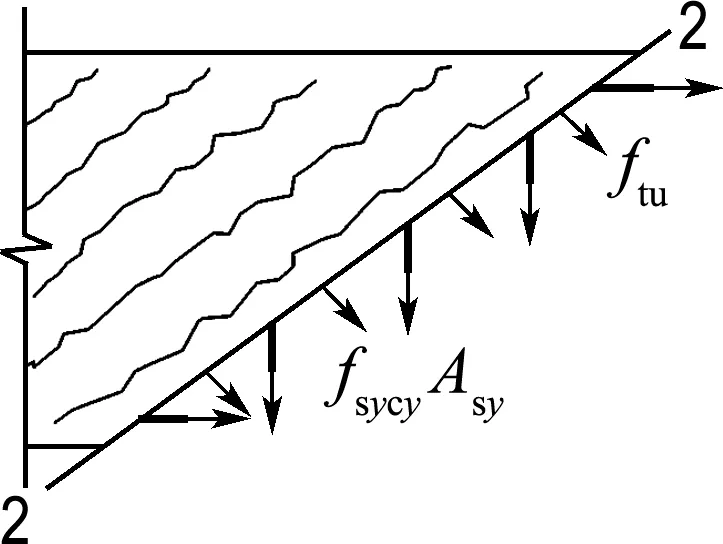
(c) 裂缝处局部应力
图6 RPC的应力分布
Fig.6Stress distribution of RPC
1.4 梁在纯弯矩作用下的受力分析
图7为纯弯矩作用下构件截面应变与应力简化图形,符合平截面假定.由于截面开裂后RPC中存在钢纤维的抗拔阻力,故不能忽略RPC的拉应力,参考文献[19]的分析方法,用集中力的方式将截面应力全部简化,见图7(e).
将梁截面压应力的曲线图形转化为等效矩形,再转化为集中力Nc,则
(24)
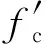
(25)
(26)
式中:εtop为梁顶受压边缘最大压应变.将中和轴下RPC拉应力曲线图形转化为等效三角形,再转化为拉力Tc,则
Tc=0.5ftbb(h-xc)
(27)
(a) 截面尺寸
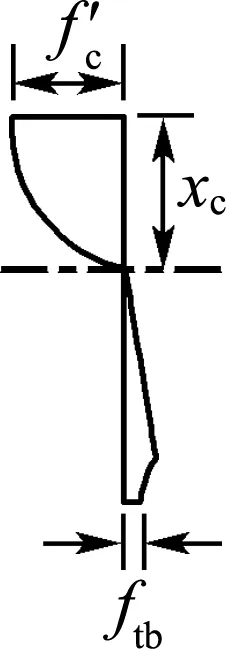
(c) RPC真实应力
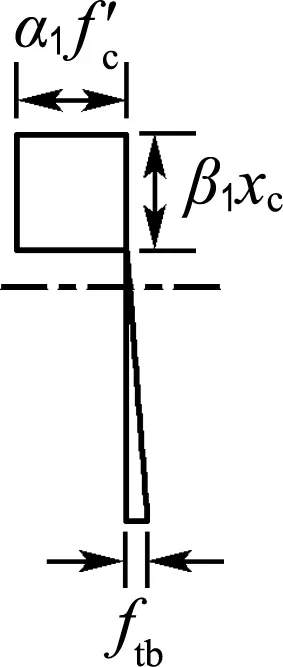
(d) 简化应力
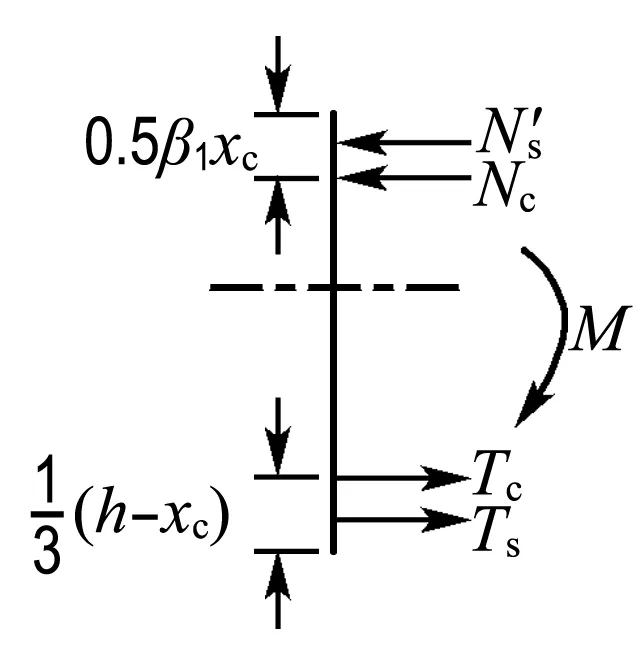
(e) 简化为集中力
图7 纯弯矩下的应力应变
Fig.7 Stress and strain under pure bending moment
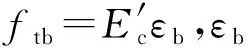
Ts=EsεsAs
(28)
(29)
(30)
(31)
(32)
(33)
(34)
截面合力Np为
(35)
1.5 弯剪共同作用下的截面分析
1.5.1 分析假定
(1)将弯剪共同作用下梁截面的剪应力图形的抛物线型简化为均布力,则εx沿截面也为均匀分布.
(2)弯剪共同作用下梁截面仍符合平截面假定.如图7(b)所示,在确定xc时叠加了剪切变形的影响,由于在纯剪作用下εx的存在,xc减小,且随着εx的增大而减小,若材料为均质弹性体,梁截面中点的应变值就是弯剪组合作用下的εx.
1.5.2 计算步骤
(1)确定截面几何尺寸及材料强度.
(2)给定初始的ε1值.
(3)给定初始的θ值.
(4)给定初始的fsy值.
(5)由式(23)计算fc1max,再结合式(13)~(15)计算fc1.当ε1≤εcr时,fc1取式(13)的计算结果;当ε1>εcr时,fc1取式(14)和(23)结果的较小值.
(6)由式(20)计算V.
(7)由式(10)和(18)计算fc2.
(8)由式(17)计算fc2max,判断fc2是否小于等于fc2max,是则继续下一步,否则说明RPC达到极限抗压强度,退出计算.
(9)由式(16)、(8)和(9)分别求ε2、εx和εy.
(10)由式(11)、(12)求fsy,并与第4步中给定的fsy值比较,若相等则继续下一步,否则重回第4步,调整所给fsy的值,直至相等.
(11)由第6步计算的V以及公式M0=Va计算M0.
(12)给定一个初始的εtop,由式(25)和(26)求α1β1和β1.
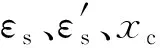
(14)由式(34)以及式(24)、(27)和(29)联合求解M,并验算M与M0是否相等,是则继续下一步,否则回到第12步,调整εtop直到满足为止.
(15)由式(21)计算Nv,由式(35)以及式(24)、(27)、(28)和(29)联合求解Np,验算Np是否等于Nv,相等则输出此时所需的变量,否则返回第3步调整θ直至满足.
(16)记录下此时数值然后返回第2步,增大ε1,进入下一个循环.
2 试验概况

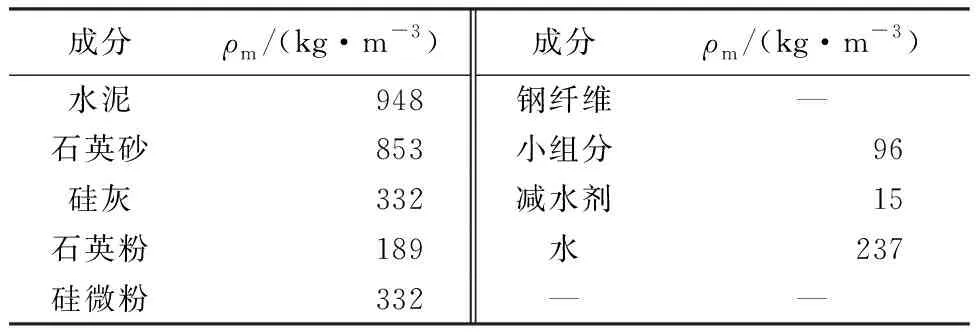
表1 RPC配合比

表2 RPC力学性能

表3 钢筋力学性能
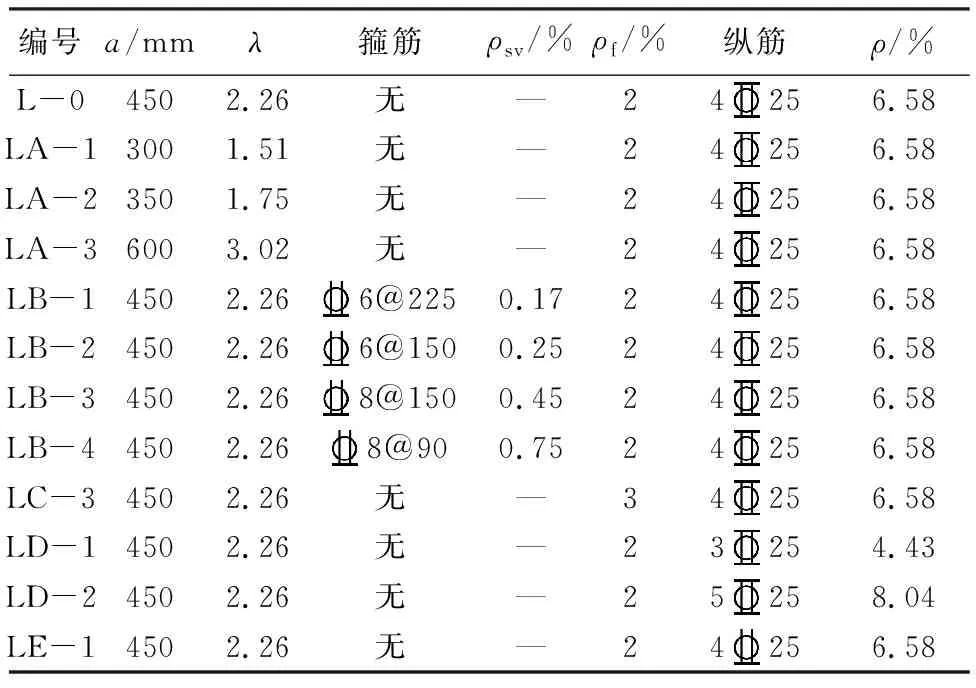
表4 试件参数
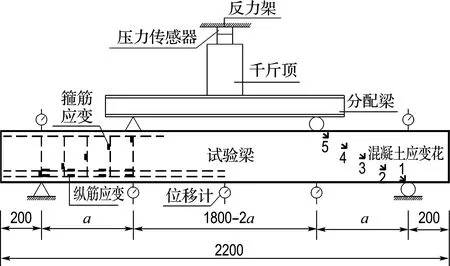
图8 试验方案及加载方式
3 结果分析
3.1 梁端剪力-箍筋平均应变关系
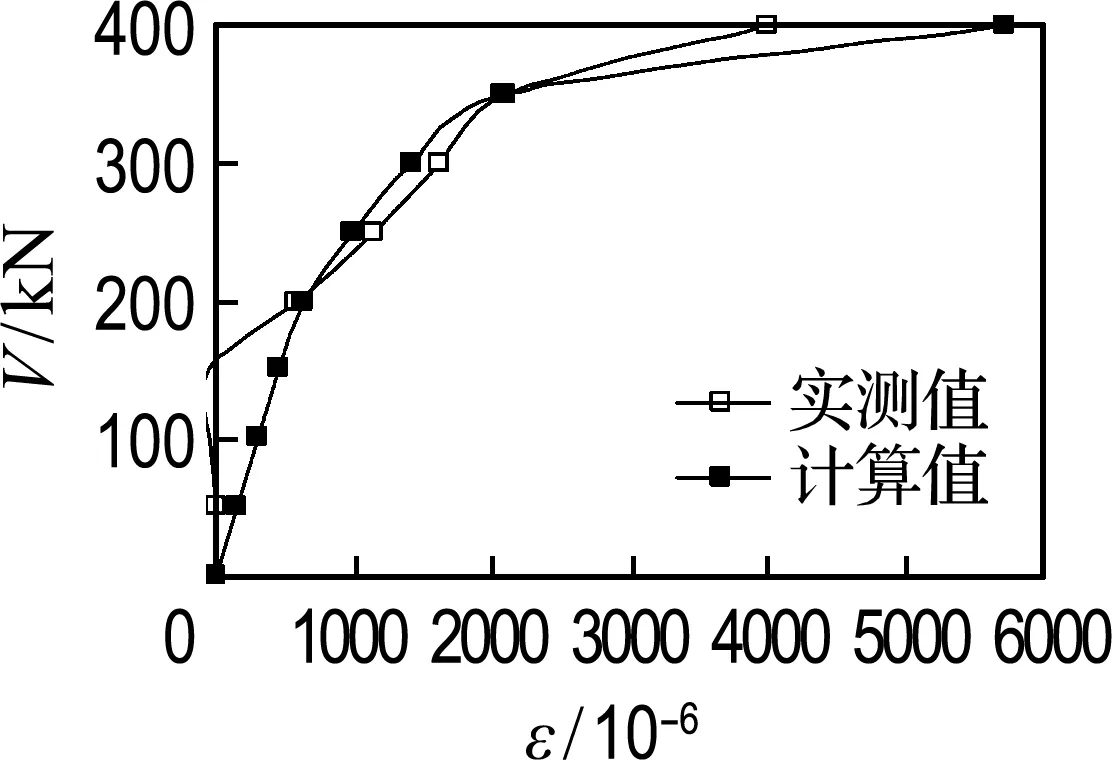
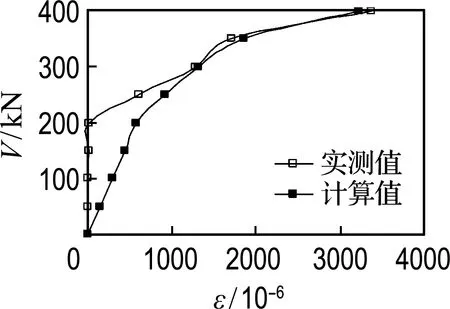
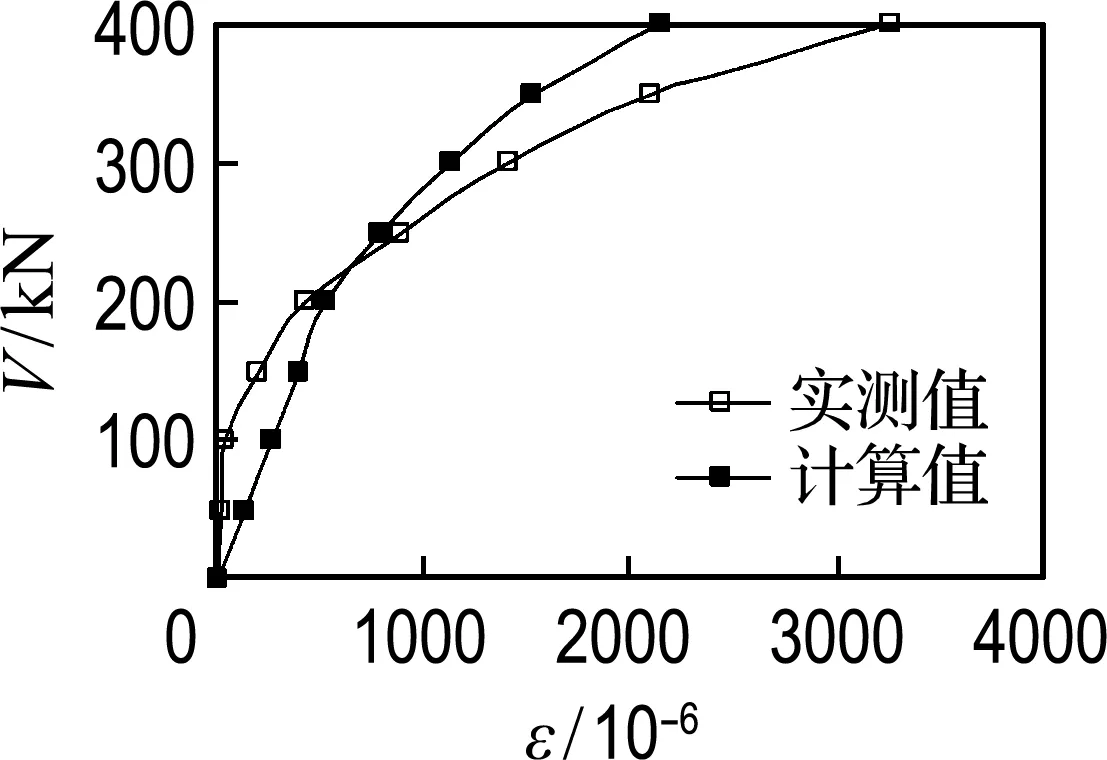
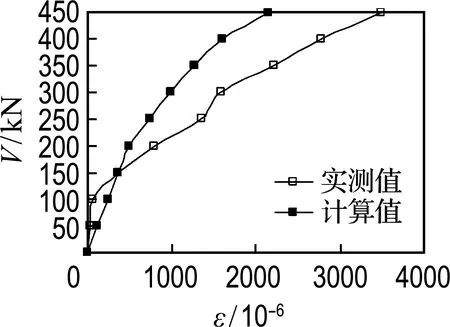
箍筋应变取加权平均值,其目的是消除加载点与支座处箍筋应变的影响,输出计算模型中各级梁端剪力对应的箍筋应变,试验梁在整个加载过程中箍筋应变实测值与理论计算值的对比见图9.
由图可得,计算值与实测值吻合较好,均能体现出随着荷载的增加,箍筋应变随梁端剪力的非线性增长趋势,并且还能体现随着配箍率的增加,箍筋应变随梁端剪力增长放缓的趋势.
3.2 梁端剪力-RPC主拉应力关系
基于B组试验梁数据,输出各级梁端剪力所对应的RPC主拉应力数值,其变化规律见图10.
将图10与RPC受拉本构关系以及文献[16]中的试验现象描述进行对比分析可得出以下结论:
(1)试验梁的开裂机理为RPC主拉应力达到材料的极限抗拉强度,开裂荷载主要与RPC的极限抗拉强度有关,且随着材料抗拉强度的增大而增大.
(2)截面出现斜裂缝后,由于RPC中存在钢纤维的抗拔阻力,开裂截面的拉应力仍能保持较高的强度,从而使得构件具有较好的延性与韧性.
(3)箍筋可以起到延缓裂缝开展的作用,随着配箍率的提高,RPC的残余主拉应力,即钢纤维的抗拔阻力下降速度变慢,直到构件快破坏时,其下降速度才变快.
3.3 极限承载力分析
将MCFT的计算结果与实测值进行比较,见表5.其中,Vcu为MCFT的计算结果,Vex为抗剪承载力实测值,公式中材料强度均取实测值.
由表5可以看出,MCFT计算值与实测值吻合良好,但也存在如下问题:
(a) LB-1
(b) LB-2
(c) LB-3
(d) LB-4
图9 箍筋应变随剪力的变化
Fig.9Variation of stirrup strain with shear force

图10 剪力-RPC主拉应力(B组)
(1)该模型更适用于以剪压破坏形态为主的试验梁,对于剪跨比较小、破坏形态接近于斜压破坏的试验梁,没有充分考虑到加载点与支座之间RPC斜压柱的有利影响,造成极限承载力的低估.

表5 基于MCFT的计算值与实测值比较
(2)模型没有考虑纵筋消栓作用的影响.表中抗剪承载力随配筋率的增加而微弱增加的原因是因为纵筋参与了弯剪承载力中的抗弯,且由文献[19]可知,弯矩对剪力的影响十分有限,故在本模型中,配筋率与纵筋强度对极限承载力的影响也十分有限.
对比文献[21]中的塑性理论、《混凝土结构设计规范》(GB 50010—2010)[22]以及《美国ACI规范》[23]的计算结果,并结合剪跨比、配箍率、配筋率以及纵筋强度(A、B、D、E组试验梁)的影响,分析各方法对抗剪承载力计算结果以及对结果趋势预估的情况,见图11.
对比各影响因素下不同计算方法的结果,文献[22]和[23]的计算结果偏保守,但能较好地估算出箍筋增强抗剪承载力的趋势.塑性理论与MCFT的计算方法对抗剪承载力的预估较精准,但在计算结果的趋势上,MCFT与试验结果更加吻合.
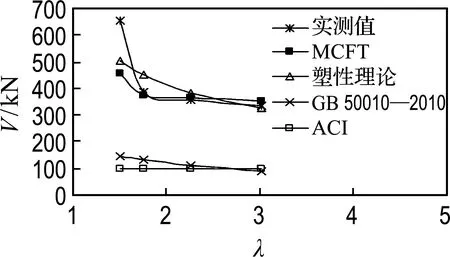
(a) 剪跨比
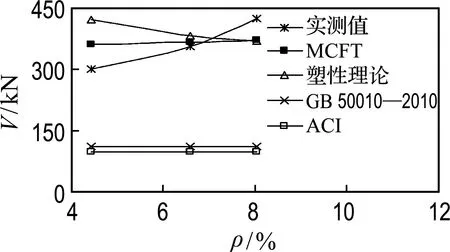
(c) 配筋率
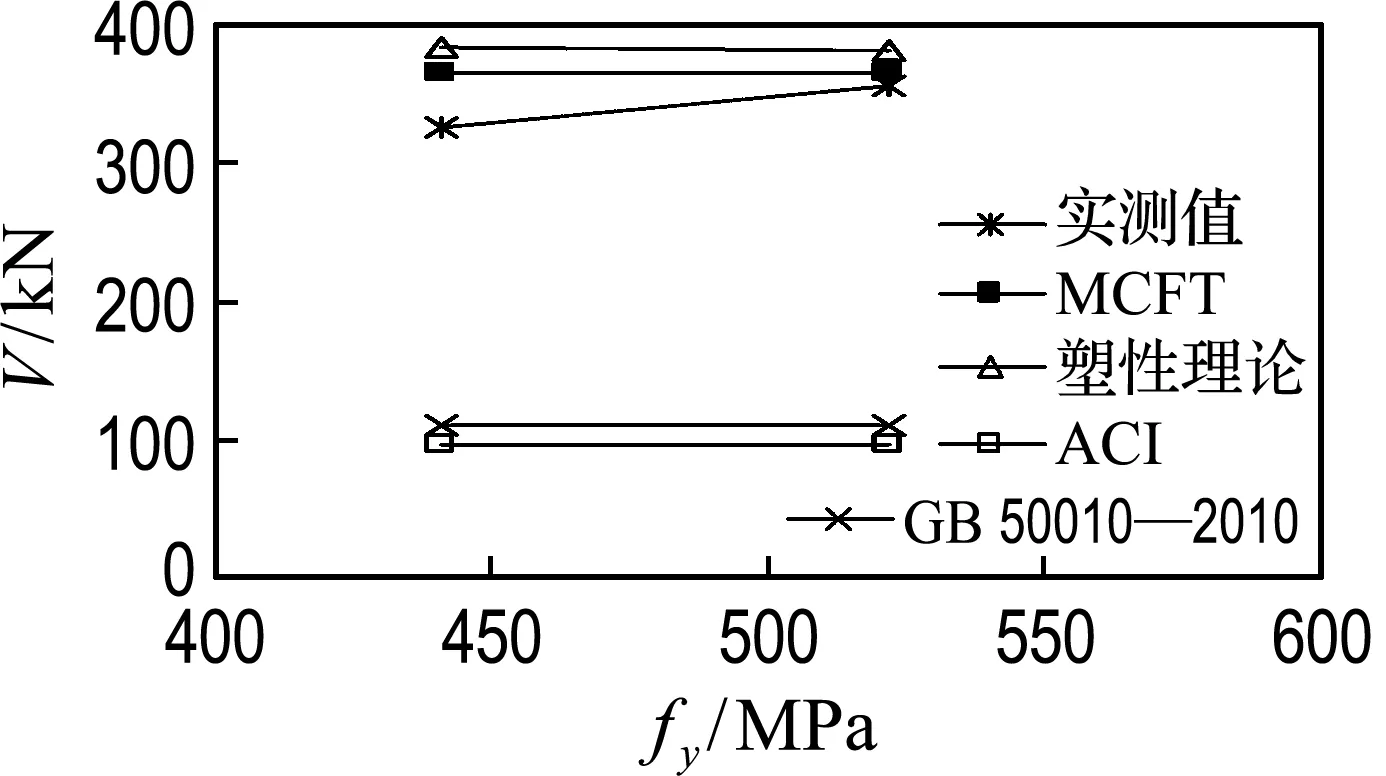
(d) 纵筋强度
图11 各影响因素下不同模型预测的抗剪承载力
Fig.11 Prediction of shear capacity under different influencing factors by different models
4 结 论
(1)基于MCFT的弯剪复合作用下截面分析模型能很好地模拟计算配筋RPC梁弯剪段的整个受荷过程,模型预估的箍筋平均应变随荷载的变化规律与实测情况较为符合,能表现出受荷后期弹塑性变化的趋势.
(2)在计算跨越裂缝的力的平衡时,由于RPC去粗骨料而含有钢纤维的材料特性,原本普通混凝土粗骨料的咬合力则被RPC中钢纤维的抗拔阻力所代替.模型预测的精准性受RPC的受拉本构关系的影响较大,不仅直接影响计算构件的开裂荷载,还可根据该关系估算出破坏时截面上残留的平均拉应力,从而为评估构件延性性能创造条件.
(3)基于MCFT预测的配筋RPC梁抗剪极限承载力与实测值的误差较小,优于现行规范,且从对4种影响因素(剪跨比、配箍率、配筋率和纵筋强度)所得结果的走势上看,还略优于塑性理论的计算结果.
(4)该模型更适用于以剪压破坏形态为主的构件,由于未充分考虑到加载点与支座之间RPC斜压柱的有利影响以及纵筋消栓作用的影响,会低估剪跨比较小、破坏形态接近于斜压破坏构件的极限承载力,同时也未体现纵筋对极限承载力的影响.
