FRP筋材加固矩形截面混凝土柱的极限强度分析
2018-11-22郭容宽唐迎春饶晓文
郭容宽 唐迎春 饶晓文
(1.广西机电职业技术学院,南宁 530007; 2.广西财经学院,南宁 530003)
0 引 言
纤维增强复合材料(Fiber Reinforced Polymer)以其轻质、高强、耐腐蚀等优越的性能,广泛地应用于工程结构加固领域中。在FRP加固混凝土结构的各种技术中,外贴FRP片材加固法因其具有施工简单、加固效果易于把握等优点,被广泛地应用于各类结构构件的加固中,尤其在加固柱、桥墩等方面应用越来越广泛[1]。因此,对FRP约束混凝土柱力学性能的研究也成为了目前结构加固领域研究的热点之一[2-4]。
在结构工程中,钢筋混凝土柱作为竖向承重的主要构件,其受力承载性能尤为关键,往往决定了整体结构工程的安全性能,钢筋混凝土柱的受损破坏通常将直接引起整个结构的破坏和倾覆,造成巨大人员和财产损失。在建筑结构出现抗力衰减、承载力不足、功能减弱时,使用者往往会更加关心对钢筋混凝土柱的加固、修复。当采用外贴FRP法加固矩形混凝土柱后,其能够有效约束受压状态下矩形截面混凝土柱的侧向变形,迫使矩形柱由轴向受压转变为三向受力状态,从而能提高混凝土的抗压强度与变形能力[5]。
就目前而言,国内外学者越来越重视对 FRP 约束混凝土矩形柱力学性能的研究:Amir Mirmiran等[6]进行了7根FRP 管约束混凝土柱轴心受压试验,对FRP管约束混凝土柱稳定性能、长细比限值等问题进行了较为详细的研究。Azadeh Parvin等[7]对9根单向碳纤维复合材料壳约束混凝土方柱的偏心受压性能进行了试验研究,对约束柱的应变梯度进行了试验和数值分析。试验中考虑了偏心率和壳厚对混凝土偏心受压强度和应变的影响。李静等[8]进行了CFRP 和GFRP 加固混凝土矩形柱的试验,发现试件的破坏有斜剪和轴压破坏两种形式,而后对两种材料混合使用后的加固效果问题进行了研究。李忠献等[9]研究了轴压比、FRP 用量、配箍率、加载顺序对CFRP 布加固混凝土短柱抗震性能的影响。
敬登虎[10]在对试验数据分析的基础上,得出了FRP约束方形截面混凝土强弱约束临界点计算式,给出了强、弱约束情况下的极限应力、应变回归分析式,提出了FRP约束方形截面混凝土的抛物线段加直线段应力-应变关系模型。Lam等[11-12]在对试验数据分析的基础上给出了FRP布约束圆形和矩形截面混凝土的应力-应变关系模型。
然而,上述研究的对象绝大多数并非正真正意义上的矩形柱,相互之间差别较大,无论是基于箍筋约束混凝土矩形柱体强度模型还是基于试验结果的经验模型,在预测FRP约束混凝土矩形柱强度方面尚未取得统一的认识,需要对其进行进一步地研究,从而给出较为合理的强度计算模型和本构关系模型。
本文在已有文献基础上,基于ABAQUS有限元软件,构建FRP约束矩形截面混凝土柱轴压试验模型,分析混凝土柱应力-应变曲线,并与已有试验进行对比。在此基础上,结合侧向约束强弱界限的判定标准,推导出修正的FRP加固矩形截面混凝土柱的应力-应变关系模型,并利用已有试验曲线进行了验证,以更好地指导工程实践。
1 FRP加固矩形截面柱有限元模拟
1.1 有限元模型构建
为了研究FRP加固矩形截面混凝土柱的轴压性能,参考文献[10]中的试验,选用C30强度的混凝土和FRP材料,总共构建3组高度L为450 mm,截面宽度b为150 mm (即长细比L/b为3),截面长度a为150 mm (即截面长宽比a/b为1)的FRP加固矩形截面混凝土柱有限元模型,各组分别设置FRP加固层数为0、1、2层,其边界条件为:在三个对称面分别施加约束以限制混凝土与FRP在对称面法线方向的位移。模型的加载方式:在柱顶设立一个刚性面,刚性面和矩形混凝土柱间设置库伦摩擦力来考虑试验时加载板对混凝土柱的环箍效应。此外,由于混凝土与FRP之间的作用机理相当复杂,因此建模过程中采用在混凝土与FRP表层设置摩擦单元实现两者的粘结效应。其计算网格划分图如图1所示。

图1 FRP加固矩形截面混凝土柱有限元网格划分Fig.1 FEM of reinforced concrete columns with rectangular cross section by FRP
模型中,C30混凝土的强度为24.5 MPa,混凝土受压本构采用《混凝土结构设计规范》中给定的混凝土受压应力-应变曲线,该曲线为二次抛物线加水平直线的模型。其数学表达式为式(1):
(1)
根据大量的材料试验表明FRP为线弹性材料,因此在建模过程中,将FRP的本构模型设置为线弹性关系。根据万能试验机对FRP筋材的物理力学性质进行室内试验,得到其在建模过程中表现的基本性质如表1所示。
表1FRP筋材的物理力学性质

Table 1 Physical and mechanical properties of FRP tendons
1.2 有限元结果分析与验证
计算中,提取各组工况下模型横向应变、轴向应变与应力关系曲线,为验证本次有限元计算结果的准确性,将有限元计算提取的结果与文献[10]中的试验结果进行对比验证。其中,有限元计算所得变形、应力云图如图2和图3所示。
将数值计算得到的轴向平均应力-轴向平均应变曲线与文献[10]中的试验曲线进行对比,对比曲线图分别如图4-图6所示。由图4-图6可见,数值计算结果与文献[10]中试验结果吻合较好,轴向应力-应变曲线误差基本在10.28%之内,轴向应力-横向应变曲线的误差在13.63%之内。

图2 变形计算云图Fig.2 Deformation calculation cloud

图3 应力计算云图Fig.3 Calculation of stress in stress
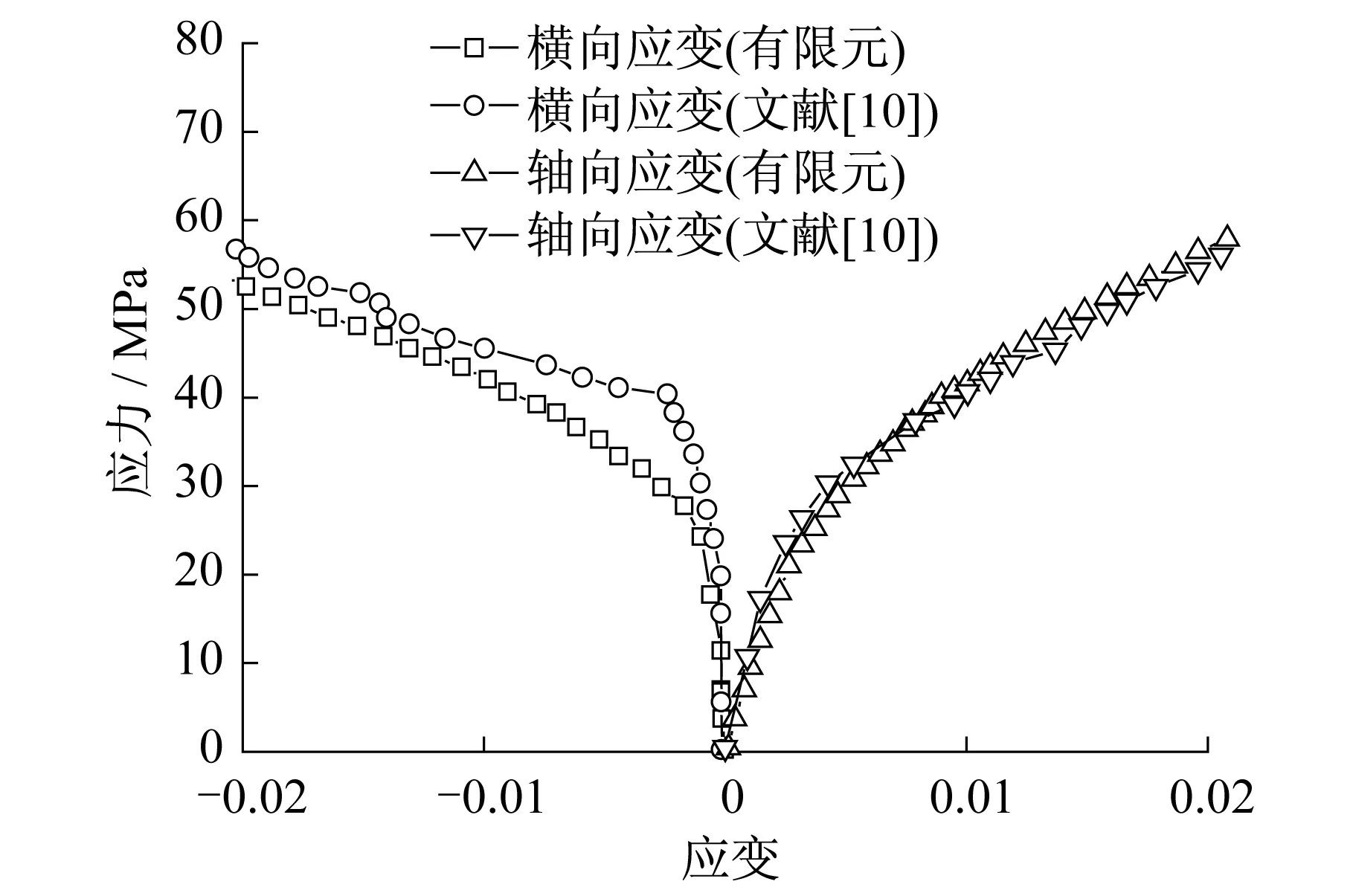
图4 轴向平均应力-轴向平均应变曲线(未加FRP)Fig.4 Axial mean stress-axial average strain curves (without FRP)
在FRP筋材约束应力达到未约束混凝土峰值应力之前,混凝土处于弹性状态,其横向膨胀变形很小,此时FRP筋材提供给混凝土的约束力较小,当约束混凝土应力超过未约束峰值应力后,此时横向应变快速增加,FRP筋材提供的约束力逐渐增大,因此矩形混凝土受到三向约束作用,承载力和变形能力都产生了较大幅度增加。

图5 轴向平均应力-轴向平均应变曲线(1层FRP)Fig.5 Axial mean stress axial average strain curves (1 layer FRP)
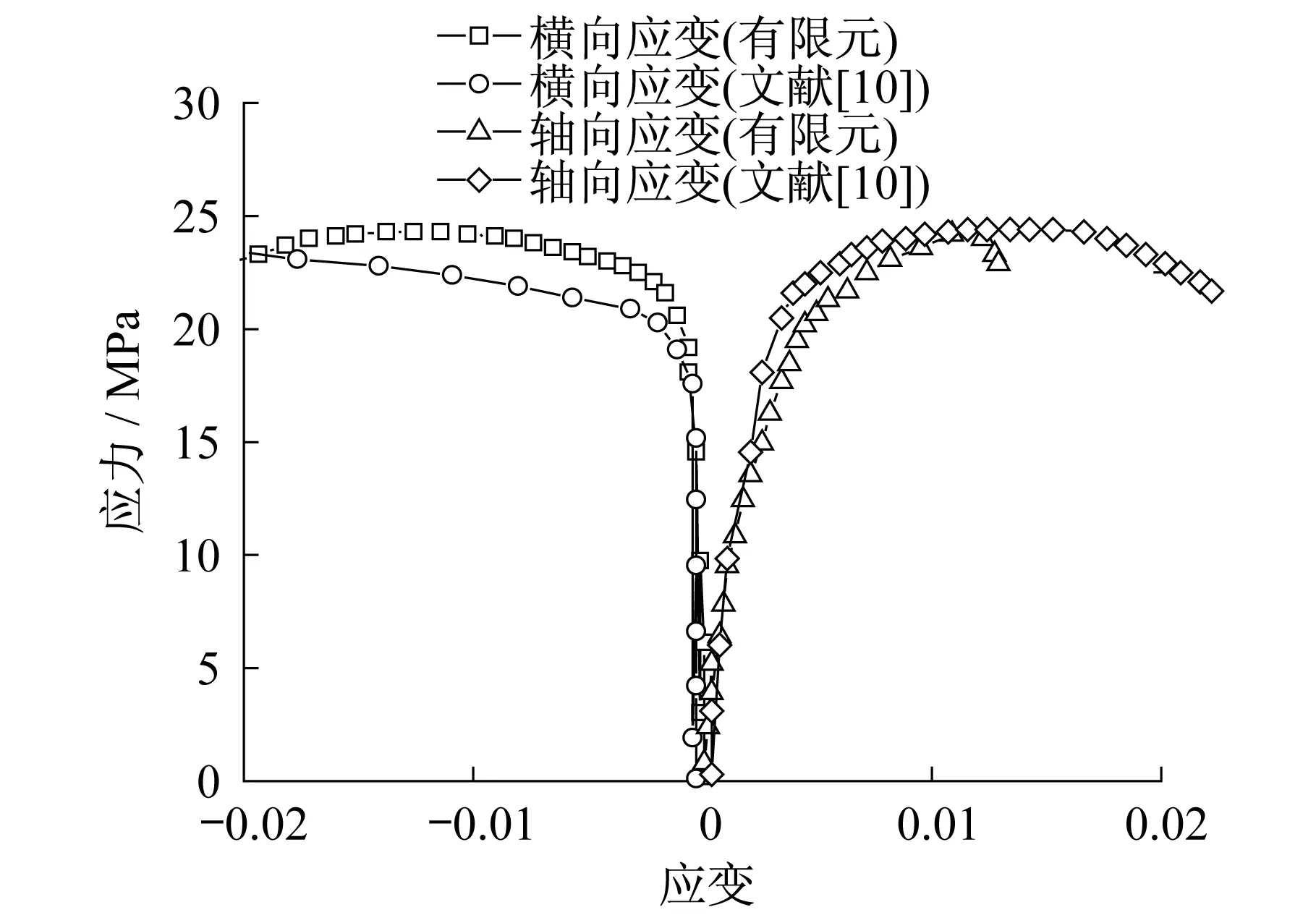
图6 轴向平均应力-轴向平均应变曲线(2层FRP)Fig.6 Axial mean stress axial average strain curves (2 layer FRP)
2 FRP加固矩形截面混凝土柱应力-应变关系
2.1 已有计算模型的局限
现有文献对于FRP加固矩形截面柱的应力-应变关系已有很多[13],纵观已有研究成果,虽然在一定条件下,这些应力-应变模型能够满足计算需要,但不可都认,大多数模型都是建立在试验研究中有限个试验数据分析的基础上提出的,具有较大的局限性,在推广使用方面还存在较大问题,还未能得到一个较普适的计算模型。
因此,下文将利用前述数值模拟方法,建立更多组不同工况下的FRP加固矩形截面混凝土柱模型(长细比L/b=2、3、4,长宽比a/b=1、1.5、2,加筋层数取0、1、2、3),将数值计算获得的应力-应变曲线进行数据拟合,从而提出一种修正的FRP加固矩形截面混凝土柱应力-应变计算模型。
2.2 截面形状系数ks
为了反映FRP约束混凝土矩形柱的截面应力不均匀的情况,往往通过定义截面形状系数来对FRP材料约束混凝土矩形柱侧向约束应力进行折减,以此反映这种截面应力不均匀的情况。目前较为普遍使用截面形状系数模型主要为有效约束面积模型,其利用有效约束面积比作为截面形状系数来降低FRP 筋材对矩形截面柱混凝土产生的侧向约束应力。
模型假定在短边的抛物线与直角边交点处的切线倾角为45°,但长边抛物线与直角边交点处的切线倾角,随着截面长宽比变化而变化。长边抛物线高度等于b/2(1-b/2d),矩形柱截面积为Ac=bd-86r2,如图7所示。

图7 有效约束面积计算示意图Fig.7 A schematic diagram of effective constraint area calculation
则FRP材料约束混凝土矩形柱的有效面积计算公式为
(2)
2.3 倒角削弱系数
经研究表明[14],FRP加固矩形截面混凝土柱时,如果不做倒角,FRP的利用率往往较低,不同拐角半径下FRP有效平均拉应力相对约束圆柱体情况时横向拉应力差异比较显著。但是仅用倒角相对大小无法直接表现出倒角对加固效果的影响,因此本文采用文献[10]给出的拐角削弱系数,其具体表达式为
(3)
式中:r为倒角半径;b为矩形截面短边长。
2.4 侧向约束应力和约束刚度
对于混凝土圆柱,在轴压荷载作用下,FRP筋材抑制、约束混凝土柱的横向膨胀变形,对混凝土产生均匀的约束压力f1(图8),其中,tfrp,ffrp分别为FRP 筋材的厚度与环向抗拉强度。
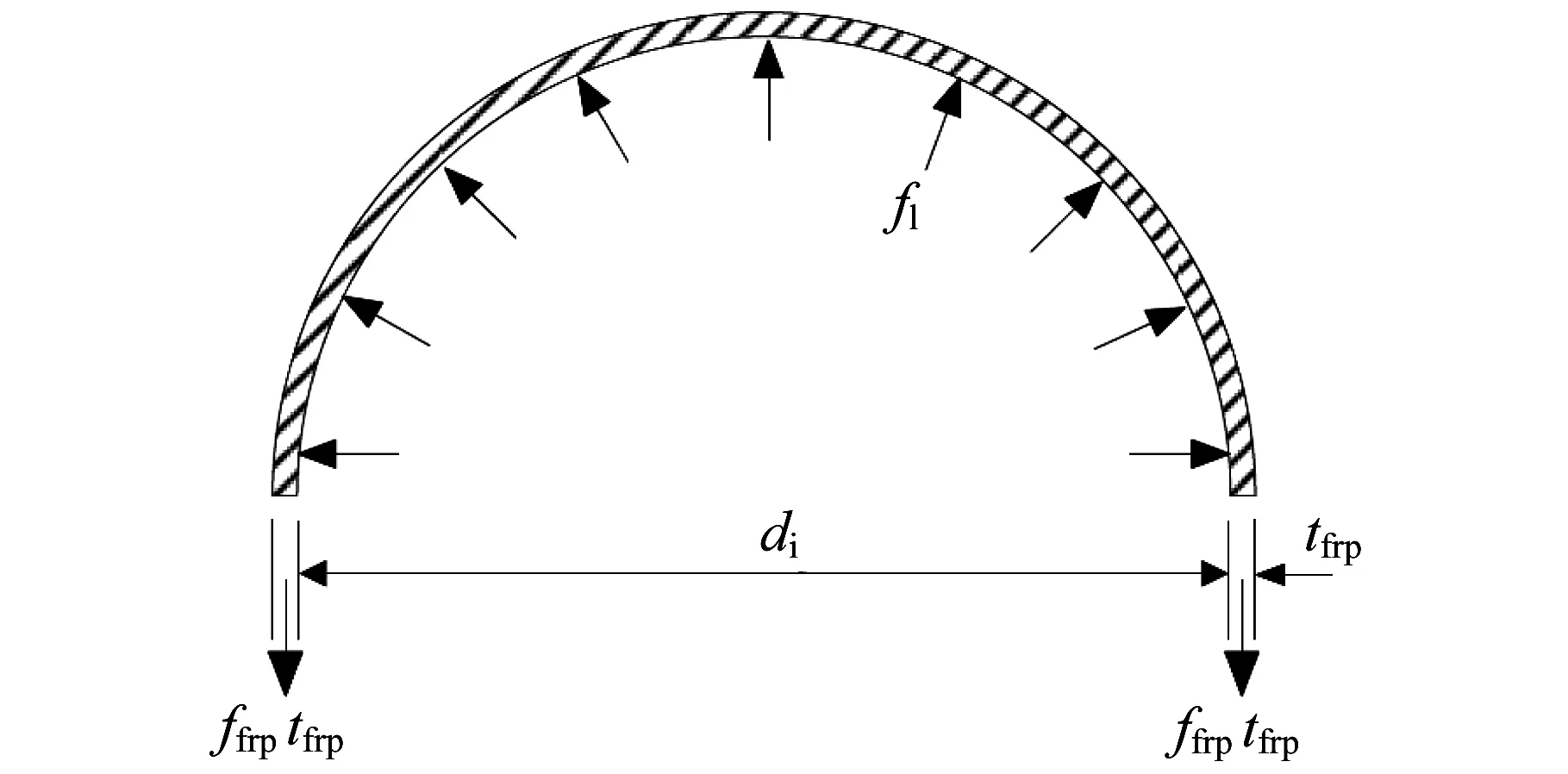
图8 FRP材料对圆柱的侧向约束应力Fig.8 Lateral confinement stress of a FRP material to a cylinder
根据静力平衡条件,FRP材料产生的侧向约束应力,可以由下面的公式求出:
(4)
(5)
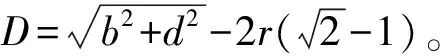
综合对各个参数的分析,FRP约束混凝土矩形柱的侧向约束应力为
(6)
(7)
2.5 强度计算模型
2.5.1弱约强度计算模型
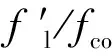
(8)
进而可以得到FRP约束矩形截面混凝土柱弱约束极限应变计算式为
(9)
图9所示为弱约束数值计算结果与文献[10]中预测模型预测结果的对比情况。从图中可以看出,数值计算构建的弱约束修正极限应力-应变计算模型精度比较合理,其绝大部分计算数值位于±18%的误差范围之内。
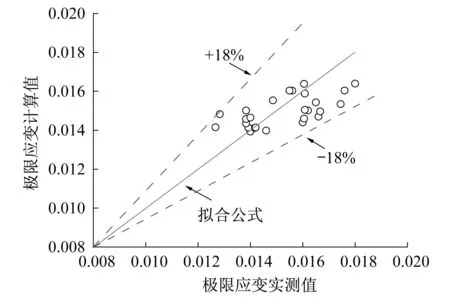
图9 弱约束极限应变数值与文献值[10]比较Fig.9 Comparison of weakly constrained limit strain values and literature[10] value
2.5.2强约束强度计算模型

(10)
进而可以得到FRP约束矩形截面混凝土柱强约束极限应变计算式为
(11)
图10所示为强约束数值计算结果与文献[10]中预测模型预测结果的对比情况。从图中可以看出,本文数值计算的强约束峰值应力和峰值应变模型有较好的精度,其大部分数值位于±22%的误差范围之内。
2.6 修正的应力-应变计算模型
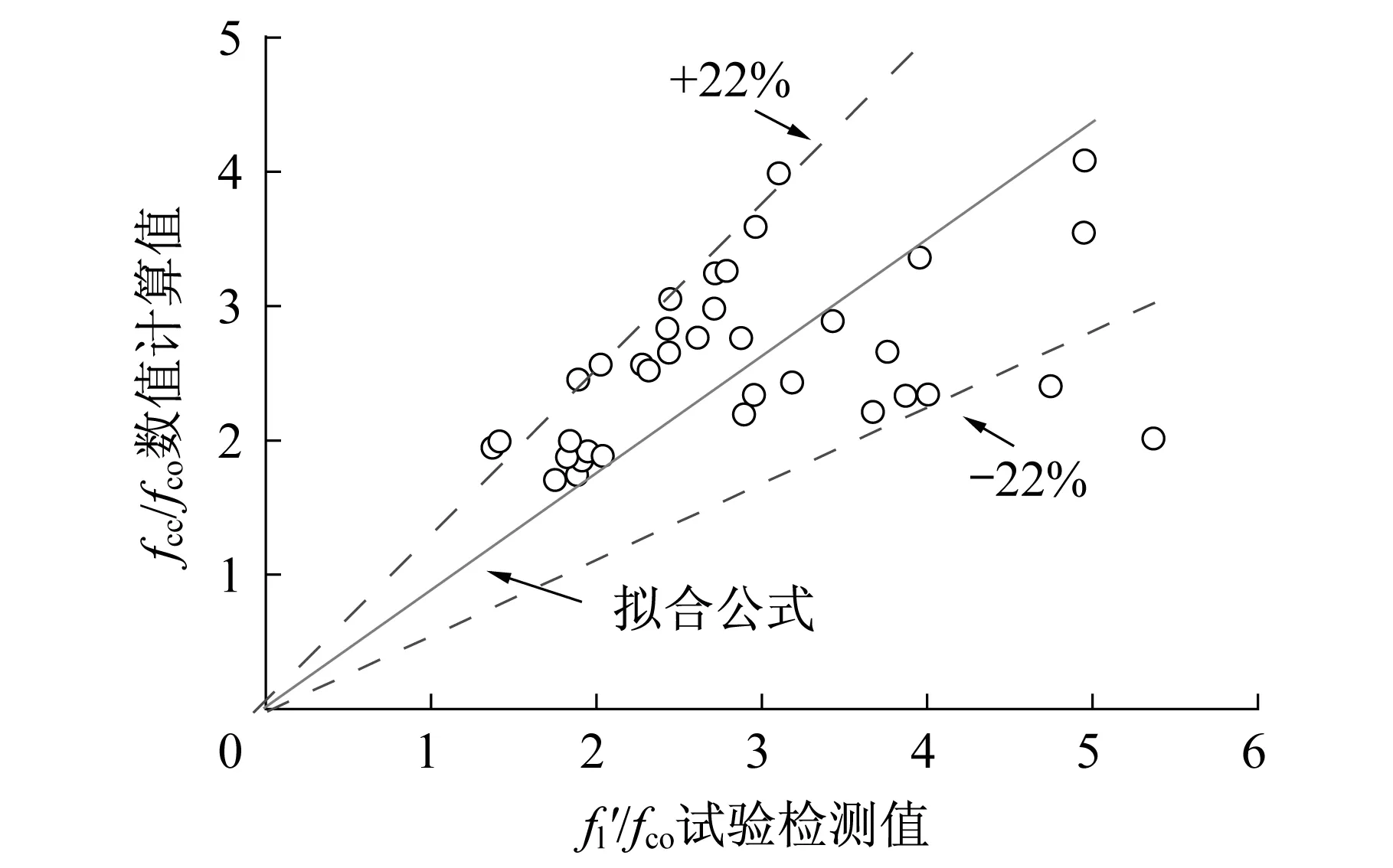
图10 强约束数值计算值与文献值[10]比较
通过对比分析文献[10]的试验曲线和数值计算结果后发现,可以将FRP约束混凝土的应力-应变曲线分为三个阶段:
(1) 弹性变形的阶段:当轴向应力较小时,混凝土未开裂,横向变形较小,FRP筋材对混凝土的约束应力也较小,FRP约束的混凝土柱的应力-应变曲线与未约束混凝土柱的应力-应变曲线类似;
(2) 弹塑性阶段:随着荷载的增加,当轴向应力超过未约束混凝土的抗压强度后,就会进入弹塑性阶段,内部混凝土开始出现裂缝,FRP筋材的约束应力迅速增大;
(3) 塑性阶段里,FRP筋材约束混凝土的应力-应变情况根据FRP筋材约束混凝土强弱可以分为强约束和弱约束两种情况,当FRP约束混凝土的能力比较强时,随着轴向压力的增大,混凝土横向变形也在增加,FRP筋材达到极限应变直至试件破坏。而当FRP约束混凝土的能力较弱时,混凝土横向变形快速增大,使得试件因FRP拉断而发生毫无征兆的断裂破坏,FRP约束的混凝土应力-应变曲线出现急剧下降段。
通过对比发现无论是强约束还是弱约束,应力-应变最终将趋近于一条直线。故本文提出的FRP筋材加固矩形截面混凝土柱的应力-应变计算模型为
σ=fcp(2(ε/εcp)-(ε/εcp)2) 0≤ε≤εcp
(12)
(13)
为验证所提应力-应变模型的准确合理程度,通过MATLAB编制相应计算程序,将文献[10]中试验获得的应力-应变曲线与本文所提模型的计算曲线进行了对比(图11),经比较可知,对于本文所提应力-应变曲线与试验曲线吻合较好,具备了一定的精度,且计算表达式结构形式简单,参数选取更加合理简便。
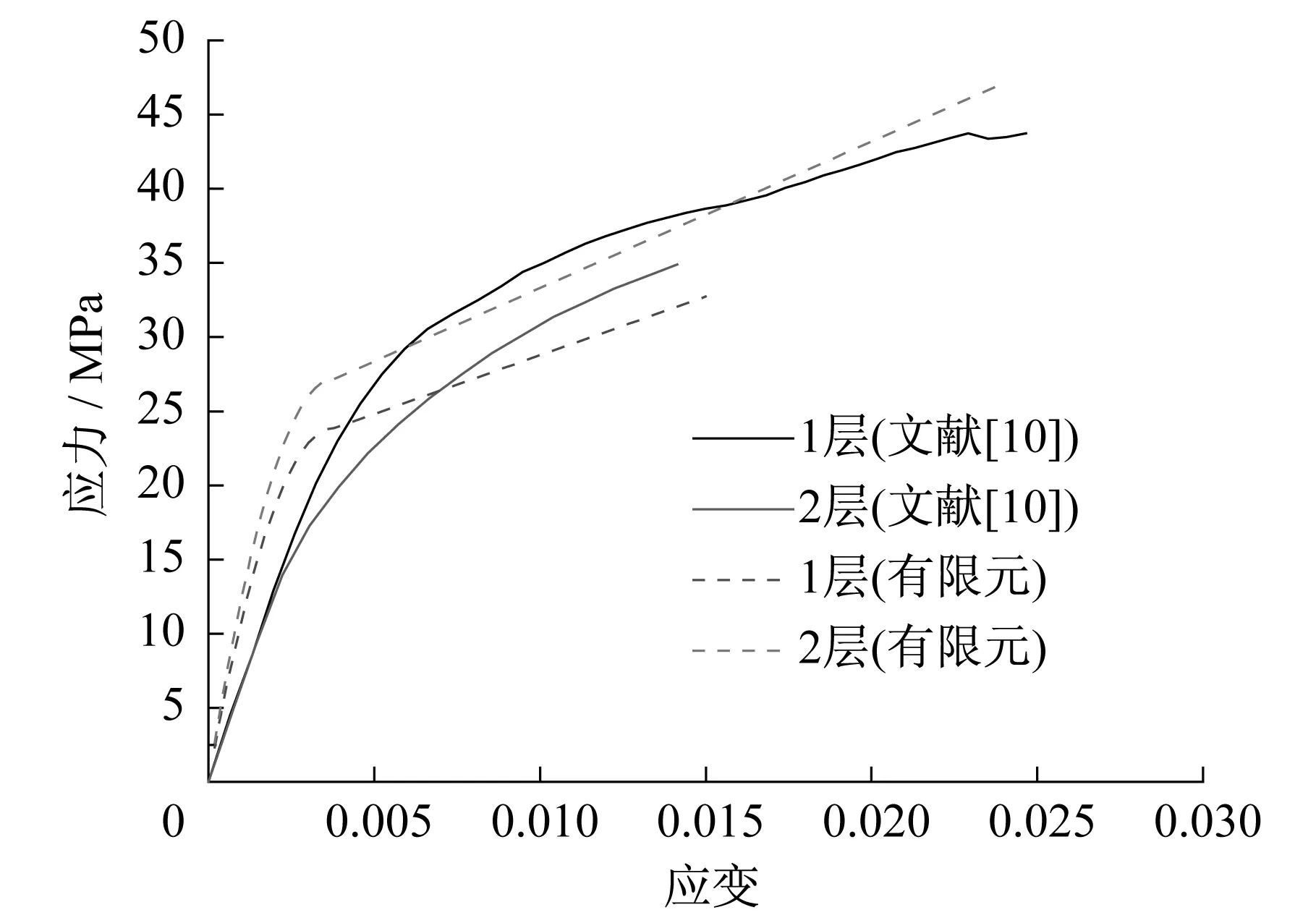
图11 本文预测曲线与文献[10]预测曲线对比Fig.11 Comparison between prediction curve of this paper and literature[10] prediction curve
3 结 论
采用ABAQUS构建了FRP筋材加固矩形截面混凝土柱承载力性能有限元分析模型,分析了FRP加固矩形截面混凝土柱应力-应变关系。结合数值模拟计算结果与已有试验结果,研究了FRP加固矩形截面混凝土柱应力-应变关系模型。主要结论为:
(1) 在FRP筋材约束应力达到未约束混凝土峰值应力之前,混凝土处于弹性状态,其横向膨胀变形很小,此时FRP筋材提供给混凝土的约束力较小,当约束混凝土应力超过未约束峰值应力后,此时横向应变迅速增加,FRP筋材提供的约束力逐渐增大,其承载力和变形能力都产生了较大幅度增加。
(2) FRP对矩形截面混凝土柱的约束效果主要取决于混凝土横向膨胀性能和FRP的横向约束能力,由于约束作用改善了构件的延性,提高了构件的承载力。
(3) FRP约束混凝土的应力-应变曲线分为弹性阶段、弹塑性阶段以及完全塑性三个阶段,当FRP约束力较弱时,混凝土横向变形快速增大,引起FRP拉断而发生急剧断裂破坏,FRP约束的混凝土应力-应变曲线出现下降段。
