钢管混凝土抗冲击性能研究现状及计算建议

王潇宇 肖 岩 徐金俊

(1.湖南大学土木工程学院,长沙 410082; 2.南京工业大学土木工程学院,南京 211816)

0 引 言

钢管混凝土(Concrete-filled Steel Tubes,CFST)结构具有承载能力高、塑性和韧性好、抗震性能优良、施工方便以及经济性能良好等优点,目前已在高层及超高层建筑、大跨度桥梁、电力基础设施等领域得到越来越广泛的应用。这些工程结构多数为一个国家或地区的重大建设项目,且直接与生命线工程相关,一旦发生诸如倒塌、坍塌等破坏性事故,必将造成重大财产损失和威胁人民的生命安全,因此,防灾减灾事业任重而道远。除地震、海啸等自然灾害外,撞击和爆炸是由人为因素而引起的一类高频灾种,其破坏程度不亚于自然界施加于人造设施的破坏力,这些人为灾害更需要引起科研工作者、工程设计人员、政府管理部门的重视。由于钢管混凝土结构具有良好的力学性能,尤其是抗变形能力较强,这已引起有关学者对其抗冲击性能方面的研究兴趣,目前国内外对钢管混凝土柱抗冲击性能的研究越来越多,大致可分为抗轴向冲击和抗侧向冲击两类研究方向。为了将这些研究成果及时地展现给学界同行,本文系统地梳理了现今有关钢管混凝土柱抗冲(撞)击性能的试验方法、试验结果、数值技术以及理论模型,同时对未来钢管混凝土柱抗冲击性能的研究给出了相关建议。

1 轴向冲击性能

1.1 研究现状与分析

迄今为止,国内外对钢管混凝土构件轴向抗冲击性能方面的研究主要为快速加载试验机加载试验、霍普金森杆加载试验、重力式落锤试验机加载试验,通过试验研究揭示其在轴向冲击荷载下的动态力学性能与破坏机理。

1) 快速加载机加载

采用快速加载试验机进行冲击加载试验的特点在于易于控制加载过程,但加载速率较低,不适合用于研究在高应变率下构件的动力效应,适应于低应变率下的加载试验。陈肇元等[1]利用快速加载试验机对钢管混凝土试件进行了快速加载试验,应变率为60×10-3～ 75×10-3s-1,同时为方便对比,该课题组还进行了钢管混凝土短柱的轴向静力加载试验以及混凝土材料和钢材在快速变形下的强度试验。研究结果表明:与静力加载相比,快速加载下钢管混凝土短柱的轴向受压强度提高了约20%,其提高幅值与混凝土抗压强度提高幅度17%和钢材强度的提高幅度20%相当。Lahlou等[2]利用MTS试验机对钢管约束高强混凝土试件完成了快速轴向压缩加载试验,加载速率为3.6×10-3～ 6.5×10-3s-1,试验发现随着钢管对混凝土约束程度的提高,钢管混凝土的轴向动态抗压强度增加明显,同时延性也得到显著提高。

2) 霍普金森杆加载

霍普金森杆装置的优点是可以实现构件在高应变率下的冲击加载试验,并能较好地控制应变率,易于操作,试验成本较低;但其缺陷也是十分明显的,目前仅能对尺寸较小的构件进行加载,主要用于材料层面的冲击力学性能测试。Xiao[3]采用霍普金森杆装置对钢管混凝土圆柱体试块进行了冲击加载试验,并提出了钢管混凝土动态增大系数(DIF)的简化计算公式和动态约束系数的概念;基于试验测试,得到钢管混凝土圆柱体试块的动态增大系数DIF与计算公式所得的DIF较为接近;同时,试验结果还表明钢管混凝土的动态约束系数与相应的静态约束系数较为相近。Huo[4]对小尺寸钢管混凝土试块在经历不同温度场后进行了霍普金森杆冲击试验,探索了高温后钢管混凝土抗轴向冲击荷载的性能,由此发现,随着温度的升高,钢管混凝土的动态强度显著降低。此后,何远明等[5]进一步利用大尺寸的霍普金森杆装置对高温下钢管混凝土试块进行了轴向冲击试验,发现了钢管混凝土试块在冲击荷载下高温劣化作用明显,温度越高,钢管混凝土试块的极限强度越低;但动态增大系数DIF随着温度的升高先略有下降之后又呈现出增长的趋势。

3) 落锤实验机加载

重力式落锤试验机加载是冲击试验最常用的方法,其优点在于直观、原理简单、易于控制、使用灵活、应用范围广泛等。国内外许多学者采用了落锤试验机对钢管混凝土进行了轴向冲击试验。

Prichard和Perry[6]对1.2 mm、3.0 mm、5.0 mm和6.3 mm四种不同壁厚的钢管混凝土短柱进行了落锤冲击试验,采用了3.2 m/s、4.4 m/s、6.3 m/s三种速度,落锤重量为82.5 kg。试验结果表明随着钢管壁厚的增大,冲击力峰值略有增大;而同等壁厚下,冲击速度的增大对冲击力峰值的提升更为明显。

Xiao和Shen[7]利用落锤试验机对2 mm、4 mm两种不同壁厚的钢管混凝土柱进行了轴向冲击试验,并与约束钢管混凝土短柱做了对比研究。试验结果显示:在相同冲击荷载下,钢管壁越厚冲击力峰值越大,残余变形越小,尤其是环向残余变形减小得越明显,可见钢管对混凝土的环向约束效应明显。

霍静思等[8-9]对13根不同壁厚的钢管混凝土短柱试件在经历不同高温后进行了落锤轴向冲击试验,研究了不同温度和钢管壁厚对钢管混凝土轴向抗冲击性能的影响,结果表明:经历高温后,钢管壁较薄的试件斜向剪切破坏程度明显;随着温度的升高,钢管混凝土的动态增大系数DIF呈现出先增大后减小的趋势,但总体比常温下的动态增大系数DIF有所提高;随着壁厚的增加,钢管混凝土的轴向残余变形显著减小。

钢管混凝土轴向冲击试验汇总情况见表1,表中各试验的试件截面类型均为圆形截面,暂时未发现其他类型的截面的试验报告。由于不同学者对钢管混凝土抗轴向冲击性能研究的侧重点不同,所选取的影响因素也往往有所差别,综合来看,主要有以下几类影响因素:冲击速度(应变率)、构件尺寸、温度、钢管对混凝土的约束程度等。通过对各研究进行细致的梳理归纳,将普遍性的研究结论总结如下:

(1) 钢管混凝土轴向冲击力随着应变率、套箍系数的增大而增大,应变率对轴向冲击力的提高尤为明显;

(2) 随着温度的升高,钢管混凝土轴向的动态增大系数DIF呈现出先增大后减小的趋势,但总体比常温下的动态增大系数DIF有所提高;

(3) 钢管壁厚的增大能显著改善钢管混凝土构件在轴向冲击荷载作用下的变形性能,壁厚越大残余变形越小。

表1钢管混凝土柱轴向冲击试验信息汇总表

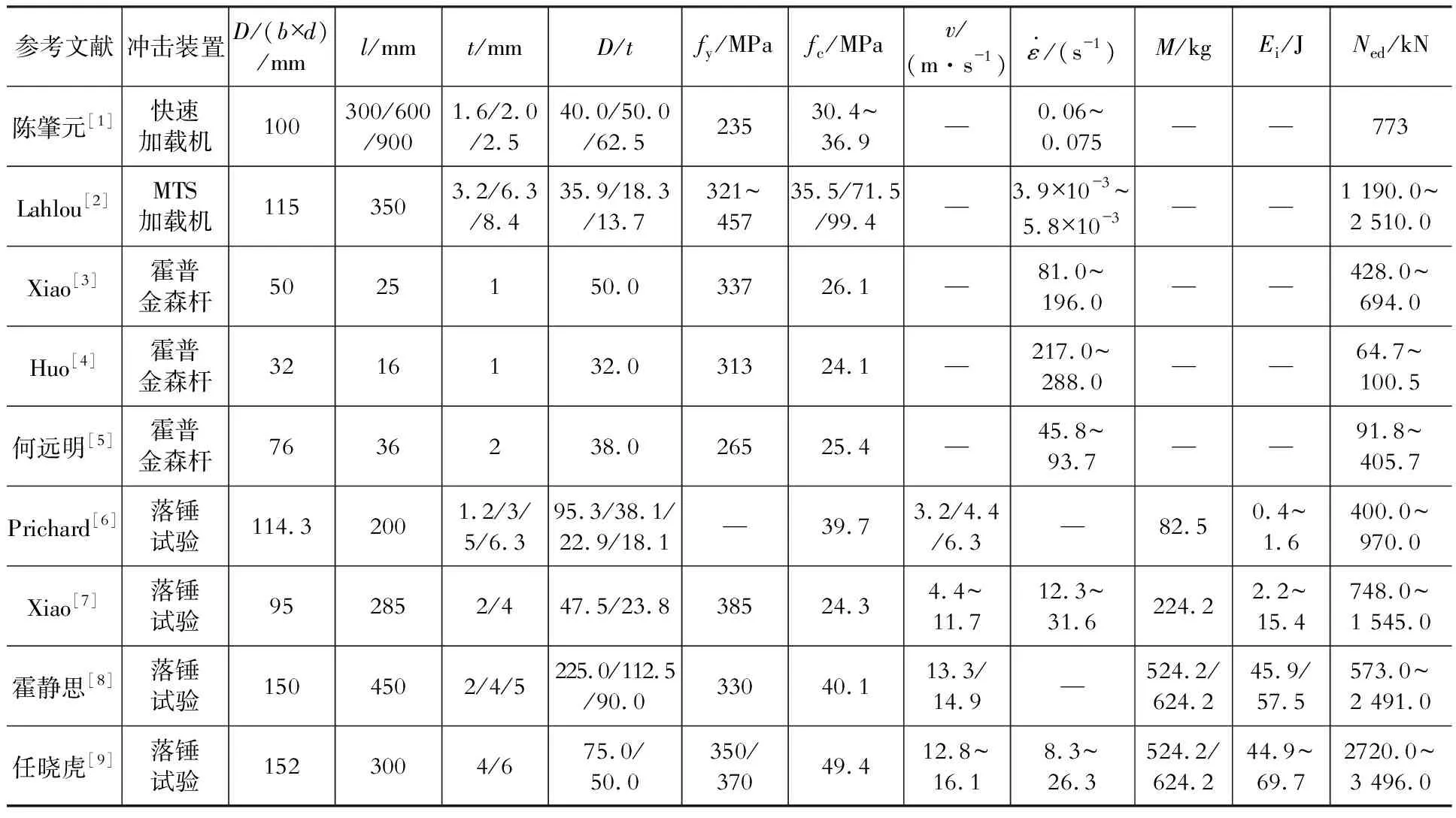
Table 1 Summary of axial impact test information of concrete filled steel tubes

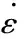
1.2 轴向冲击承载力计算建议

本文将以往研究者的研究成果进行总结对比,分析了钢管混凝土轴向冲击承载力的应变率效应。

在动力荷载作用下,钢材和混凝土都存在应变率效应,即材料强度随着应变率的增大而提高。在20世纪90年代,Bischoff和Perry[10]总结了各个学者对混凝土动力抗压性能研究方面的主要成果,提出了混凝土受压动态增长系数随应变率成指数型增长规律,并且发现高应变率和低应变率存在不同的增长趋势。CEB-FIP规范[11]中根据试验数据拟合得到的计算公式也将混凝土应变率效应分成高应变区和低应变区,见式(1)。另外关于钢材的应变率效应,目前已经发展出了许多相关力学模型,其中最有代表性的为Cowper和Symonds[12]提出的Cowper-Symonds模型,见式(2)。

(1)

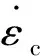
(2)

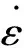
对于参数D和q,Jones[13]给出了各种金属材料的Cowper-Symonds模型参数D和q的取值,可釆用D=40,q=5。

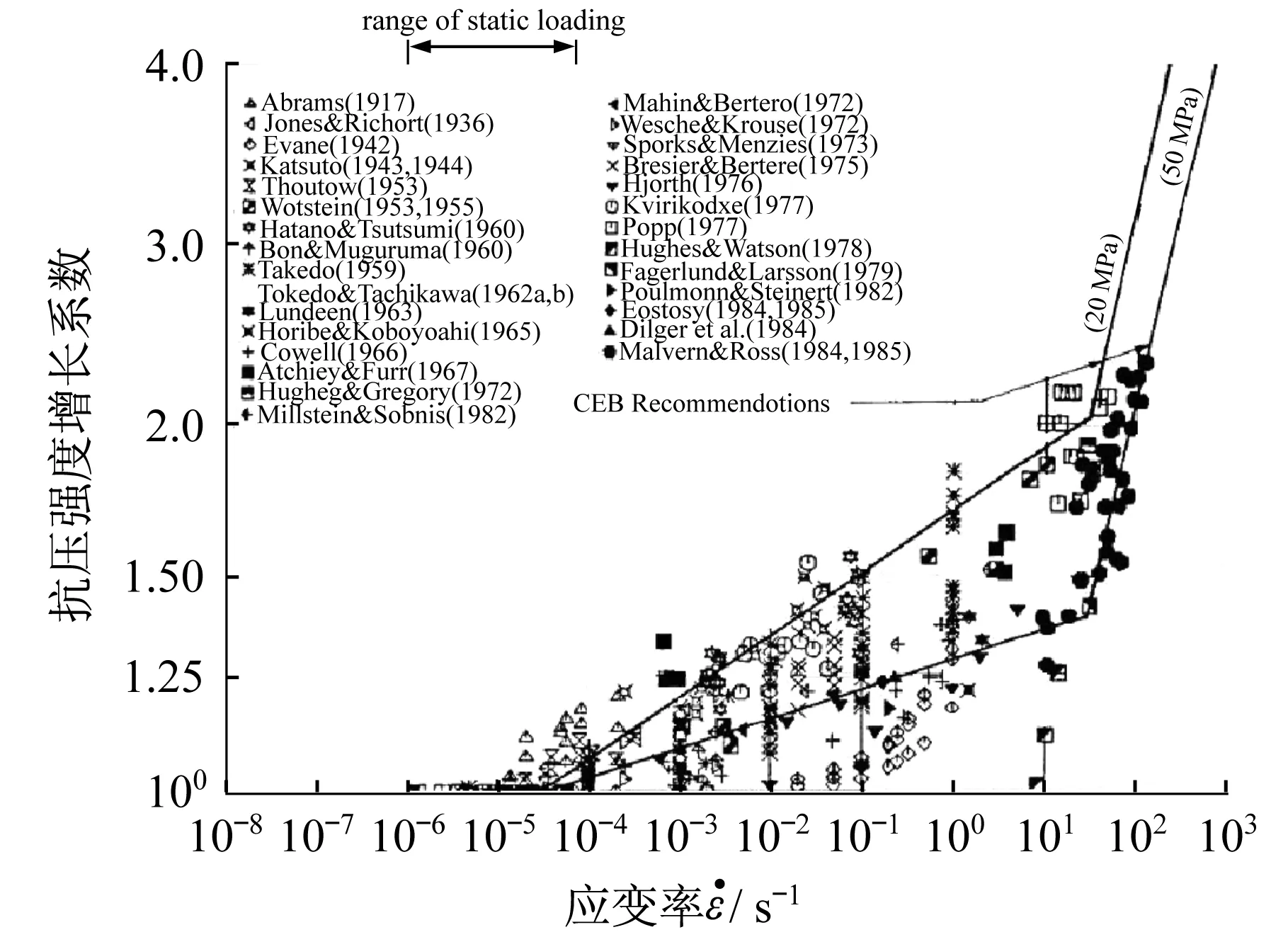
图1 混凝土受压应变率效应[10]Fig.1 Strain rate effect of concrete

为了探索钢和混凝土两种材料组合下的钢管混凝土应变率效应规律,归纳分析了上述文献中关于钢管混凝土试件轴向承载力应变率效应的试验研究结果。采用文献[1-3,5,8]中29个常温下钢管混凝土试件的试验数据,对其动态放大系数DIF和应变率之间的关系进行回归分析。为便于比较,按照文献[14]中给出的转化系数将混凝土强度统一转化为轴心抗压强度进行计算。图2为钢管混凝土轴向承载力动态放大系数与应变率对数之间的关系曲线,如图所示,在对数坐标系下,钢管混凝土轴向承载力在高应变率下的增长趋势比在低应变率下的增长趋势更为明显,这与混凝土强度的应变率效应一致。

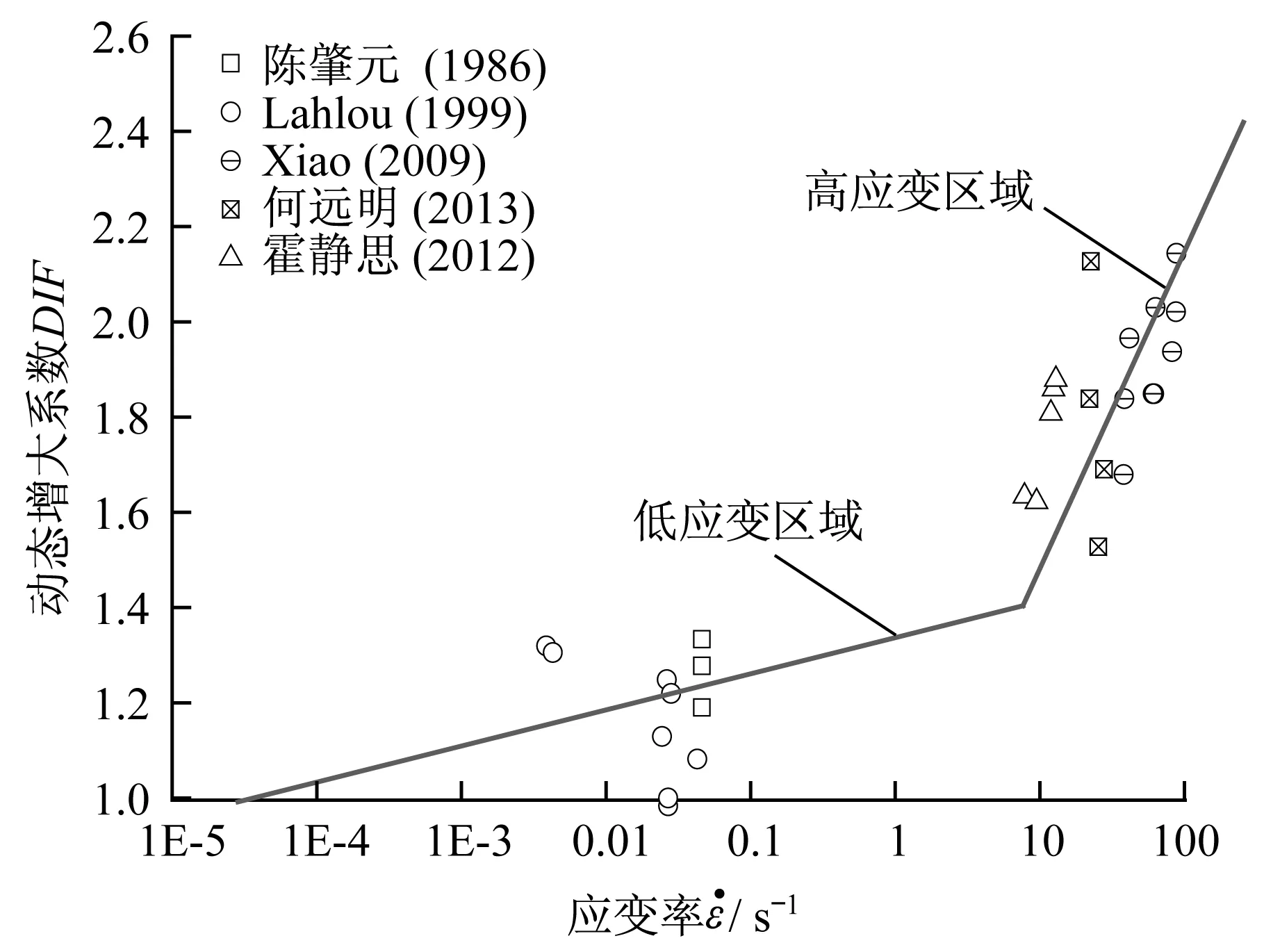
图2 钢管混凝土柱轴向受压动态增大系数与应变率关系Fig.2 Relationship between Dynamic Increasing Coefficient and Strain Rate of CFST under Axial Compression

根据上述结论,不妨假设钢管混凝土构件的应变率效应是混凝土应变率效应和钢材应变率效应的叠加。基于此思想,采用中国规范GB 50936—2014[15]提出的钢管混凝土构件静态轴向抗压强度计算公式(3),再将公式(1)和式(2)计算得到的混凝土动态强度fcd以及钢材的动态强度fyd分别代替公式(3)中的混凝土静态强度fc和钢材静态屈服强度f进行计算,从而得到钢管混凝土柱轴向动态承载力计算值Ncd。

N0=(1.212+Bθ+Cθ2)Ascfc

(3)

式中:N0为钢管混凝土短柱的静力轴心抗压强度设计值;θ为约束系数,θ=Asf/Acfc,其中,f和fc分别表示钢材的抗压强度和混凝土的抗压强度,另外Asc=As+Ac,As和Ac分别为钢管和管内混凝土的面积;对于圆形实心钢管B、C取值见式(4)和式(5):

B=0.176f/213+0.974

(4)

C=-0.104fc/14.4+0.031

(5)

为了检验该计算方法的合理性,将文献[1-3,5,7,8]试验测得的42个钢管混凝土试件的动态承载力Ned与计算值Ncd进行比较,比较结果见图3。由图3可见,计算值与试验值的比值k=Ncd/Ned的平均值为1.09,变异系数为17.05%,表明计算值与实测值接近且离散性不大。建议在一定的概率保证率下,可采用该计算方法进行钢管混凝土柱受轴向冲击承载力预测。

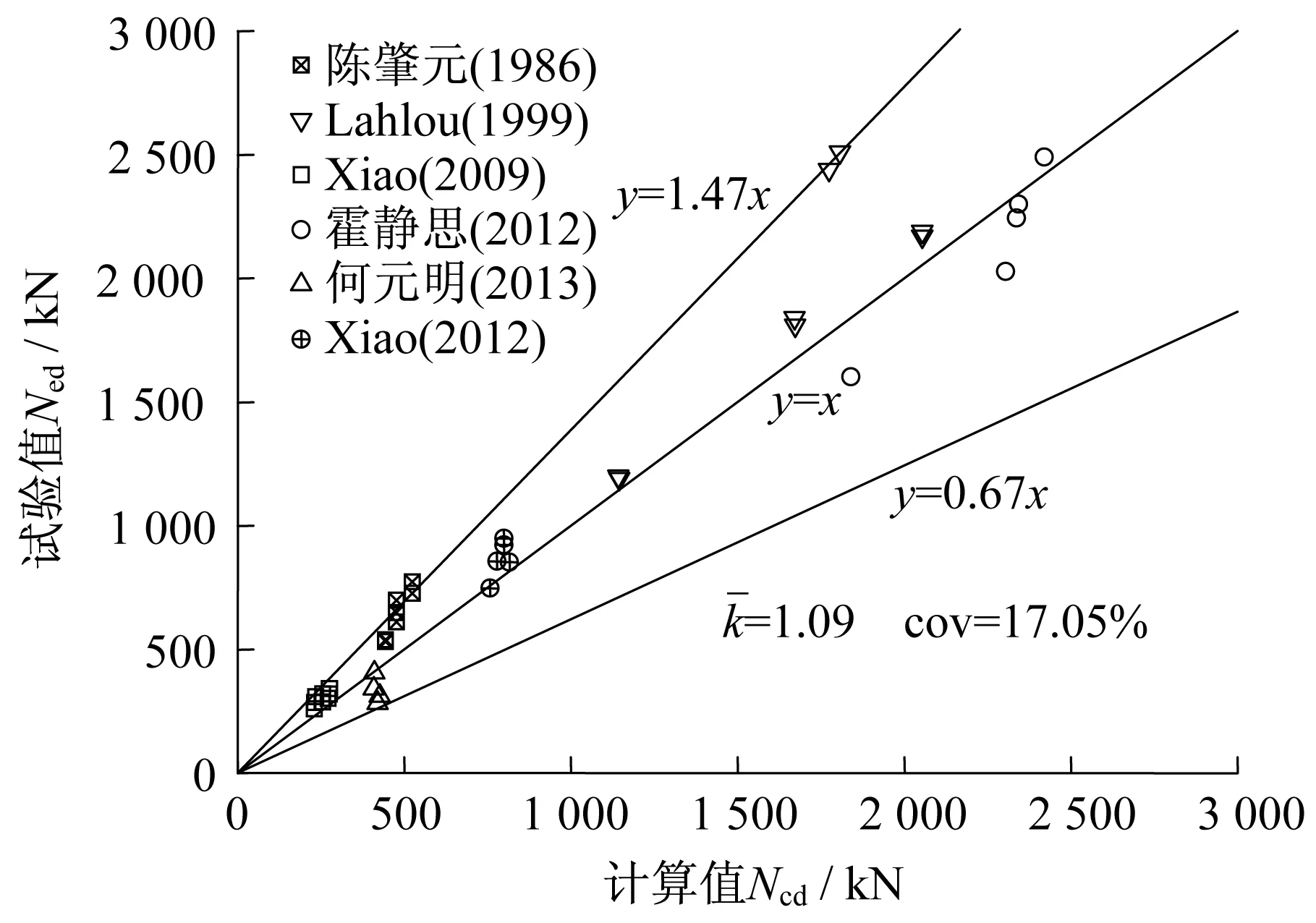
图3 轴向受压承载力计算值和试验值比值图Fig.3 Bearing capacity calculated value and experimental value ratio

2 侧向冲击

2.1 研究现状与分析

一般而言,钢管混凝土构件更易遭受垂直于构件纵向的横向冲击荷载,因此研究钢管混凝土构件在侧向荷载作用下的抗冲击性能更具有工程意义。

王蕊、任够平、李珠等[16-21]利用落锤试验机对不同壁厚的钢管混凝土构件进行了侧向冲击试验以及采用有限元计算软件完成了仿真模拟分析,研究了套箍系数、冲击速度、冲击能量、边界条件以及轴压比对钢管混凝土抗侧向冲击性能的影响,结果表明冲击力曲线可分为峰值阶段、平台阶段以及降落阶段;挠度随冲击能量的增大而增大,而随套箍系数的增大而减小;冲击力峰值和冲击力平台随套箍系数的增大而增大,相同钢管混凝土构件在不同冲击作用下的冲击力平台值变化不大,轴压比对冲击性能的影响显著;最后在试验研究和有限元分析的基础上,提出了钢管混凝土构件在侧向冲击荷载作用下挠度的计算方法。

瞿海雁[22]采用LS-DYNA有限元软件对钢管混凝土柱的侧向冲击性能进行了影响参数分析,研究了混凝土强度、钢材强度、冲击能量对冲击性能的影响,并提出了简化分析模型。

侯川川[23]、章琪[24]以ABAQUS有限元软件为平台对钢管混凝土构件的侧向冲击性能进行了数值模拟分析,研究了冲击能量、含钢率、钢材强度以及混凝土强度等参数对其抗冲击性能的影响,结果表明:冲击能量越大则冲击力持续时间越长,含钢率和钢材强度的增大能显著地提升钢管混凝土构件的侧向抗冲击能力,而混凝土强度的变化则对其抗侧向冲击能力的影响较小。

Deng[25-26]完成了12个钢管混凝土构件的侧向高速落锤冲击试验,研究了不同跨度和冲击速度对构件抗冲击性能的影响,采用能量守恒和动量守恒定理验证了试验的准确性,并提出了钢管混凝土构件抗侧向冲击的设计方法。

Remennikov[27]、Bambach[28-29]、Yousuf[30-31]对普通钢管混凝土和不锈钢钢管混凝土构件的侧向冲击进行了试验研究;Bambach[28-29]在试验的基础上进行了理论推导研究,发展了不同边界条件下冲击力和吸收能关于位移的计算设计公式;Yousuf[30-31]对所进行的一系列试验完成了ABAQUS有限元仿真分析,并采用将钢材和混凝土动态材料参数代入澳洲规范静力计算公式的方法来预测动态冲击强度,比较了不锈钢和低碳钢钢管在冲击荷载下的强度和延性。

Han等[32]利用落锤装置对高强钢管混凝土构件完成了侧向冲击试验,并采用ABAQUS有限元软件完成了参数分析,分析了不同边界条件、跨度、冲击速度和冲击质量对钢管混凝土侧向抗冲击性能的影响,并提出了动态简化模型。

Wang等[33]对不同壁厚钢管超轻混凝土构件的侧向冲击性能完成了试验研究、LS-DYNA有限元模拟以及理论推导,试验结果表明冲击力时程分为峰值、平台、降落三个阶段,钢管壁厚对抗冲击性能和弯曲变形影响很大,有限元仿真结果与试验结果符合较好,并进一步提出了冲击力-位移关系理论推导公式和数值迭代计算程序。

Shakir等[34]对钢管普通混凝土和钢管再生混凝土以及FRP增强钢管混凝土的侧向抗冲击性能进行了研究,采用落锤冲击试验探索了不同跨度、锤头形状、混凝土种类以及FRP等因素对冲击动态反应的影响,并提出了位移的计算模型并对Bambach[28]提出的冲击力计算模型进行了修正。

杨有福[35-36]对圆形和方形钢管再生混凝土构件进行了落锤侧向冲击试验,研究了不同再生混凝土骨料取代率和不同轴压比对其抗冲击性能的影响,并建立了有限元分析模型,提出了冲击力的计算方法。

表2为国内外钢管混凝土梁式构件侧向冲击试验的试验参数和结果汇总,主要的影响因素包括端部约束条件、截面形式、截面尺寸、钢管厚度、混凝土强度、钢材强度、冲击速度、冲击质量以及轴向压力等。综合现有的各研究成果,可以得到如下一致性的研究结论:

(1) 钢管混凝土构件在受侧向刚性物体冲击下的力时程曲线大致可以分为三个阶段:峰值段、平台段、降落段,如图4所示。

(2) 冲击力和残余位移随着冲击速度、冲击质量和冲击能量的增大而增大。

(3) 含钢率和钢材强度的提高对钢管混凝土构件抗侧向冲击能力的提升有显著影响,而混凝土强度的变化则对其抗侧向冲击能力的影响较小。

(4) 轴压比对冲击性能的影响显著,轴压比较低时有利于抗冲击性能的提升,而较高的轴压比会降低构件抗冲击性能。

(5) 钢管混凝土构件的变形可以分为局部变形和整体变形两部分,冲击部位的局部凹陷和鼓曲以及固定端的局部鼓曲属于局部变形,构件纵向轴线的整体挠曲属于整体变形,如图5所示。

表2钢管混凝土柱侧向冲击试验信息汇总表

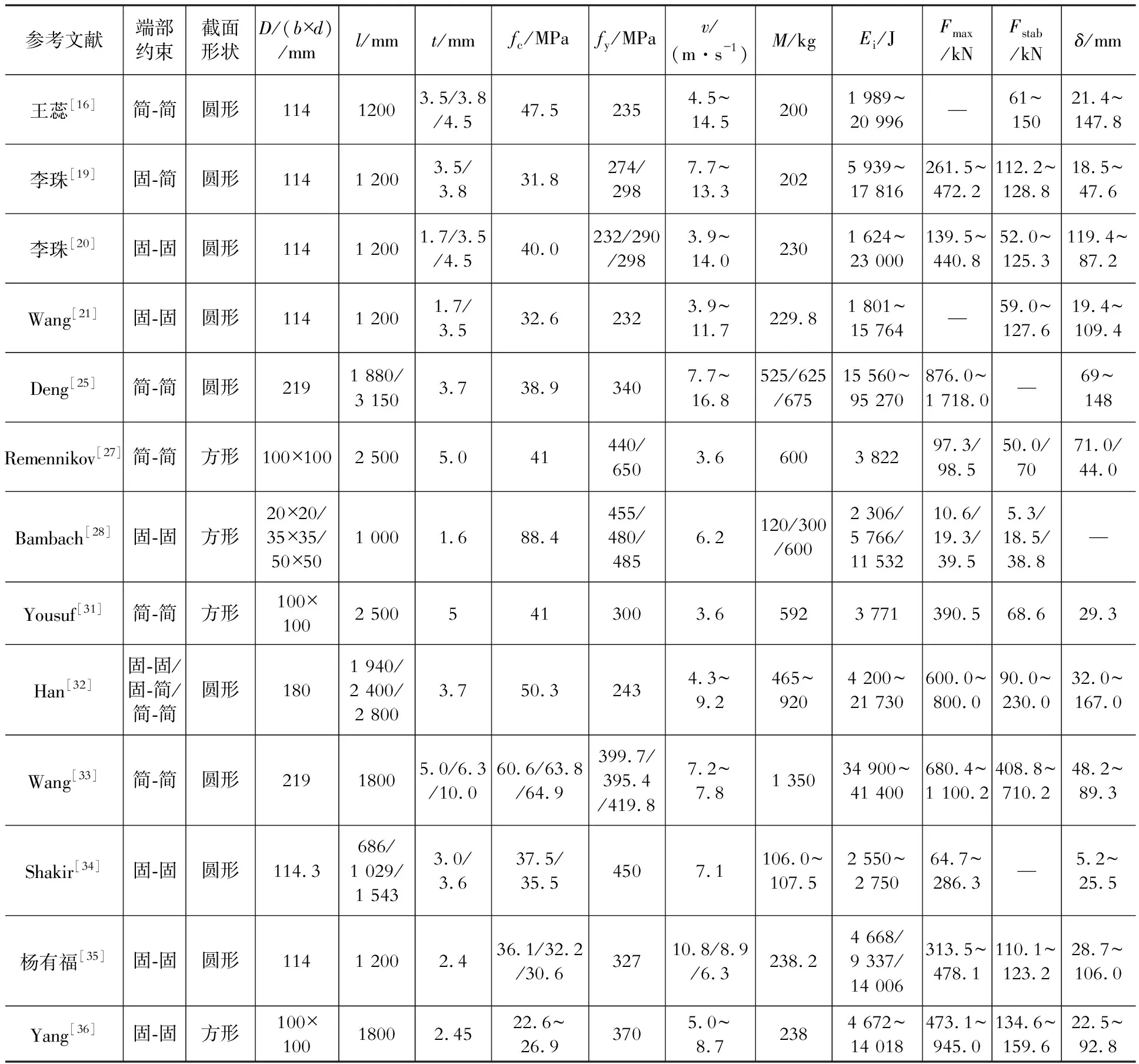
Table 2 Summary of lateral impact test information of concrete filled steel tubes

注：D为圆形截面直径;b×d为方形截面长宽;l为试件长度;t为钢管壁厚;fy为钢管钢材屈服强度;fc为混凝土轴心抗压强度(根据文献[38]进行转换折算);v为落锤冲击速度;M为冲击质量;Ei为冲击动能;Fmax为冲击力峰值;Fstab为冲击力平台值;δ为冲击点处的残余位移

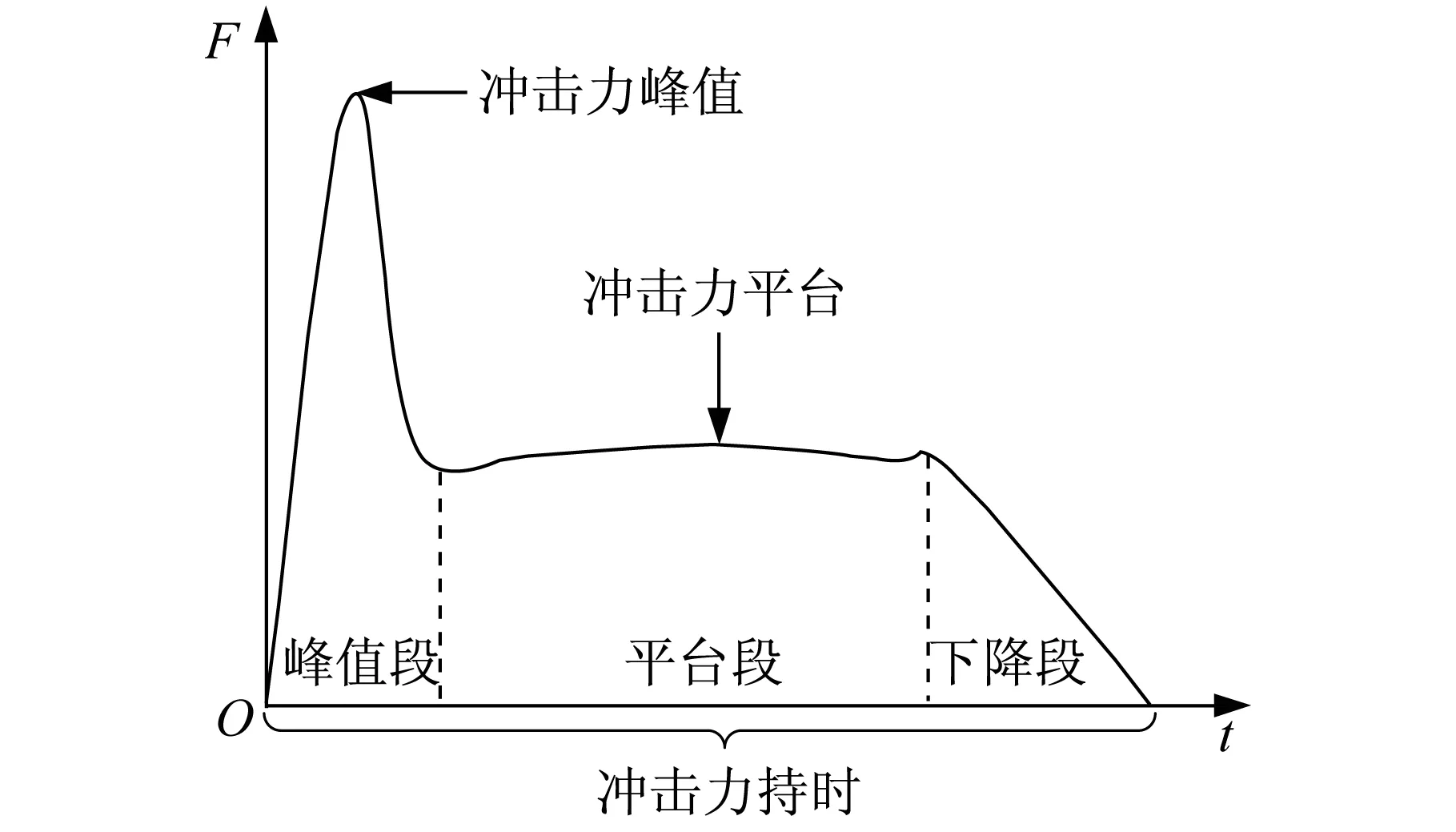
图4 冲击力时程示意图Fig.4 Time history of impact force

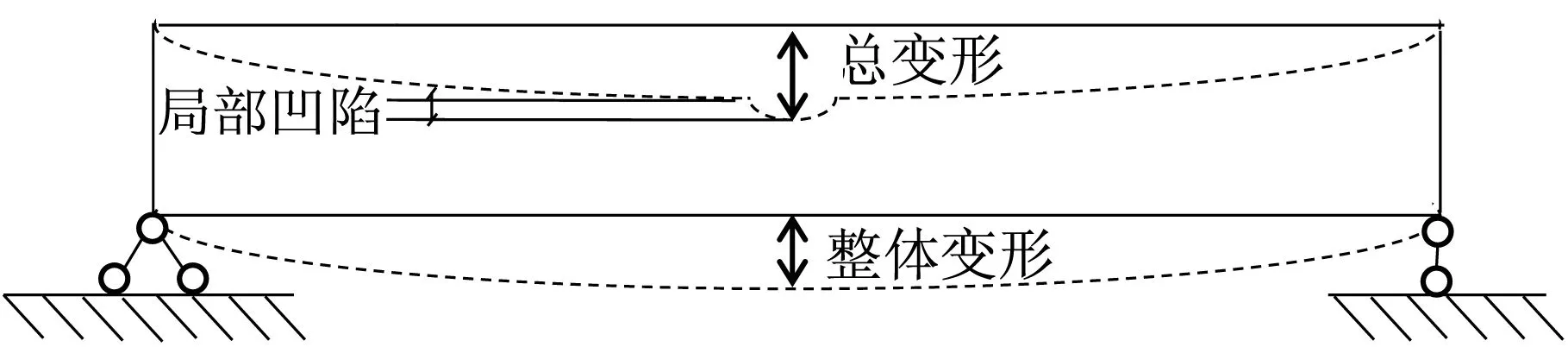
图5 变形示意图Fig.5 Deformation diagram under impact load

(6) 构件端部对自由度的约束越多,则钢管混凝土的抗侧向冲击性能越好。

2.2 侧向冲击承载力计算建议

由于冲击问题与冲击作用的属性具有很大关系,而描述冲击作用最全面的参数即是冲击动能,因此国内外学者大多从能量的角度来衡量钢管混凝土构件的抗冲击能力。本文对各学者提出的计算方法进行整合与修改,得出类似的简化计算方法,其基本流程见图6。

图6 钢管混凝土构件抗侧向冲击计算流程图Fig.6 Calculation of resistance to lateral impact of concrete filled steel tubular members

假定冲击动能Ei完全被钢管混凝土构件所吸收,而实际上冲击动能只有部分被钢管混凝土构件因变形而吸收,因此假设是偏于安全的。基于能量守恒定律,定义等效冲击承载力Feq=Ei/δ,其中,δ为冲击点处的残余位移,即冲击动能Ei等于等效冲击承载力Feq在冲击点的残余位移上所做的功。

在进行抗冲击承载力验算时,还需确定冲击力放大系数R。此处采用文献[19-21,25,32-34,37]提供的试验数据,选取其中76个经冲击试验后达到屈服但未开裂的圆形钢管混凝土试件为研究对象(即认为进入塑性状态但未丧失承载力),求得其各自的等效冲击承载力Feq。

由于本文采用的计算方法是建立在静态承载力基础之上,需要先得到钢管混凝土静态承载能力,因此采用中国规范GB 50936—2014[15]提出的钢管混凝土构件承载力计算公式(式(6)-式(9))得到其抗弯极限承载力Mu。

Mu=γmWscfsc

(6)

Wsc=πD3/32

(7)

(8)

fsc=(1.212+Bθ+Cθ2)fc

(9)

式中:对于圆形截面B=0.176f/213+0.974,C=-0.104fc/ 14.4+0.031;对于正方形截面B=0.131f/213+0.723,C=-0.070fc/14.4+0.026;θ为钢管混凝土的套箍系数,即θ=Asfy/Acfc;As,Ac分别为钢管截面面积和混凝土截面面积;fy和fc分别为钢材的屈服强度和混凝土抗压强度;D为钢管混凝土构件截面的外径;ψ为空心率,对于实心截面,取ψ=0;γm为塑形发展系数,对于实心圆形截面γm=1.2。

当不考虑剪切变形时,假设构件在相应的塑性铰出现后变为机构从而达到承载力极限状态,如图7所示,根据图7的简化分析模型计算构件在不同端部约束下的静态承载力Fu。从而求得R=Feq/Fu。图8为Feq与Fu的比值分布图,其中,R的平均值为1.87,变异系数为23.99%。基于安全设计原则,R应取较小值,假设R的概率分布为正态分布,由该样本计算可得,R取1.31时满足90%的概率保证率。此外,冲击力放大系数R受各种因素的影响,为了更加准确地进行承载力预测,需进一步进行大量的试验研究,从而更为准确地对冲击力放大系数R进行取值。

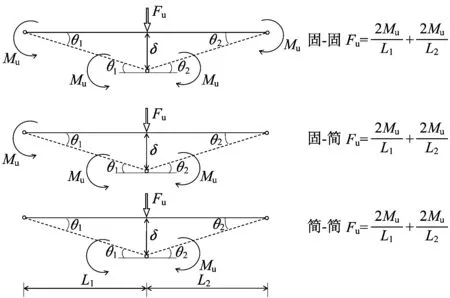
图 7 承载力简化分析模型Fig.7 Simplified analysis model of bearing capacity

3 研究的局限性

虽然国内外已经对钢管混凝土构件的抗冲击性能进行了较为系统的研究,但目前的研究也存在一些不足,具体包括以下几点:

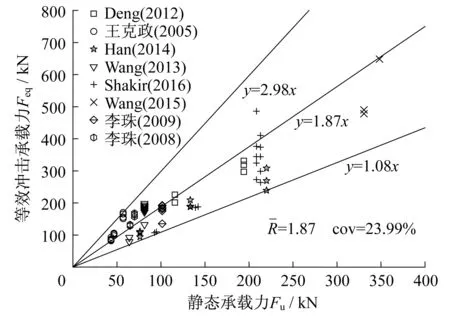
图8 等效冲击承载力和静态承载力比值图Fig.8 Equivalent impact capacity and static bearring capacity ratio

(1) 试验研究的构件尺寸较小,与实际尺寸相比,缩尺比例较大,从而导致尺寸效应影响显著。

(2) 目前的试验多为竖向垂直冲击试验,重力场方向垂直于构件轴线方向,而实际结构的钢管混凝土构件所遭受的冲击作用多为水平的车船撞击荷载,因此需要进行水平侧向冲击试验研究。

(3) 现今的冲击试验均是冲击作用点在构件的跨中,而实际结构构件在遭受车船撞击的作用点通常不在跨中,需进行不同作用点位置的冲击性能研究。

(4) 目前的研究还未涉及悬臂钢管混凝土构件的抗冲击性能研究,而悬臂构件的抗侧向刚度较小,在受冲击荷载作用下的变形会更大,因此有必要对悬臂钢管混凝土构件进行抗冲击性能研究。

4 结 论

钢管混凝土结构表现出良好的抗冲击性能,目前该方面的研究已经取得一定的成果,探讨了冲击速度、冲击质量、冲击能量、混凝土强度、钢材强度、套箍系数以及构件端部约束条件、温度等因素对钢管混凝土抗冲击性能的影响,揭示了钢管混凝土构件在冲击作用下的破坏机理,提出了一些相应的计算方法。本文首先对钢管混凝土构件轴向冲击和侧向冲击的研究现状进行了回顾、总结和对比,得到了一些具有共性的研究结论;同时也指出了目前研究的不足。此外,在现有数据的基础上,提出了钢管混凝土抗轴向冲击和抗侧向冲击的承载力计算建议,研究成果可为钢管混凝土结构的抗冲击性能研究及工程应用提供科学参考。