CFRP加固损伤混凝土梁截面短期刚度探讨分析
2018-11-22崔熙光
刘 相 崔熙光
(1.辽东学院城市建设学院,丹东 118003; 2.沈阳建筑大学土木工程学院,沈阳 110168)
0 引 言
CFRP加固混凝土受弯构件的研究国内外已经进行了大量试验研究和理论分析的工作,主要集中在其承载能力极限方面和非损伤构件抗弯刚度方面的研究工作[1-4]。但如何确定加固后特别是损伤混凝土构件正常使用极限状态方面的问题研究尚少,尤其是其截面抗弯刚度方面的研究迄今还没有很好地解决[5],即有必要对加固损伤混凝土梁短期刚度问题进行研究[6-7]。通常CFRP加固混凝土梁等受弯构件在使用阶段应具有足够的刚度,以免变形过大影响结构的正常使用。钢筋混凝土结构在其服役期间会受到不同程度的损伤,有时在加固的过程中是不卸载或部分卸载的,使得其在加固前都不同程度地存在着变形和裂缝[8],其中的纵向受拉钢筋都基本存在初始应变。此时用碳纤维布粘贴在损伤混凝土梁底面上开始并不受力,只有在新增荷载作用下才会受力。根据这种情况,本文在考虑混凝土梁在不同损伤即纵向受拉钢筋存在初始应变的条件下,通过现有试验资料的基础上,运用解析分析对相关试验数据进行拟合,给出CFRP加固损伤混凝土梁截面短期刚度的简化公式,并通过相关试验资料进行验证。
1 基本假定
(1) 碳纤维布加固损伤钢筋混凝土梁截面平均应变符合平截面假定。
(2) 不考虑混凝土的抗拉强度,全部拉力由纵向受拉钢筋和碳纤维布共同承担。
(3) 在达到受弯承载能力极限状态前,加固材料与混凝土之间不致出现粘结剥离破坏[9]。
(4) 钢筋的应力应变关系可简化为双直线模型的形式(图1)。混凝土应力应变关系采用理想化的应力应变曲线,当混凝土压应变εc≤0.002时,应力应变关系为抛物线;当混凝土压应变εc>0.002时,应力应变关系为水平线;且计算时混凝土的极限压应变εcu=0.003 3。CFRP的应力应变关系为线弹性关系[10]。
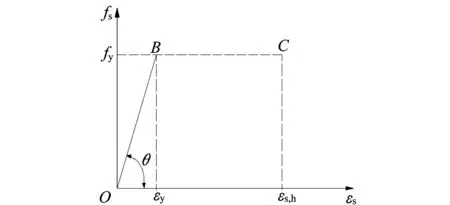
图1 钢筋应力—应变曲线的数学模型Fig.1 Mathematical model of steel stress-strain curves
(5) 钢筋混凝土梁在加固前受压区混凝土没有被压坏,符合适筋梁的破坏状态。
2 碳纤维布加固梁截面短期刚度计算
2.1 变形条件
混凝土梁在初始弯矩Mi作用下存在不同程度地损伤即受拉钢筋存在初始应变εsi;考虑二次受力影响,即碳纤维布存在滞后应变εi,在加固后正常使用阶段,开裂截面上受拉边缘总应变为
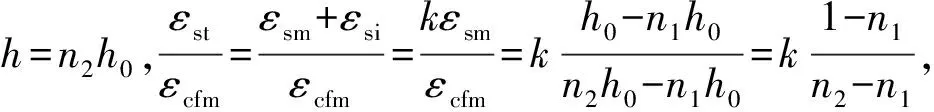
(1)
图2为截面应变分布示意图。
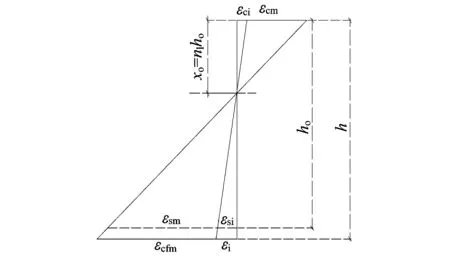
图2 截面应变分布示意图Fig.2 Sectional strain distribution diagram
2.2 本构关系
σc=εcEc=εcmλEc
(2)
σcf=εcfEcf=εcfmEcf/φcf
(3)
σs=εsEs=εsmEs/φs
(4)
式中:λ为混凝土受压变形塑性系数;φs,φcf为裂缝间钢筋、碳纤维布的应变不均匀系数;εc,εcm为裂缝截面处压区混凝土的应变及平均压应变;εcf,εcfm,εs,εsm为拉区钢筋和碳纤维布的拉应变及平均拉应变;εci,εsi,εi为加固前初始弯矩Mi作用下受压边缘的压应变、受拉钢筋的应变、受拉边缘的拉应变:
(5)
2.3 平衡条件
图3为截面应力示意图。

图3 截面应力分布示意图Fig.3 Sectional stress distribution diagram
(6)
M=(ηh-a)σsAs+ηhσcfAcf
(7)
式中:ω为压区混凝土应力图形的完整系数;η为裂缝截面上最大的力臂系数。
把式(5)代入式(7)得,
(8)
由式(6)、式(8)整理得
(9)
把式(5)、式(8)代入式(9)整理得
(10)
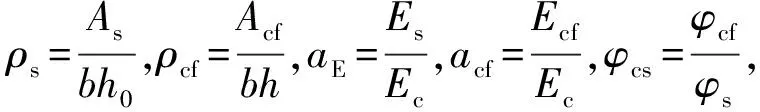
则截面平均割线刚度
(11)
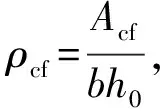
(12)
2.4 Bs值的讨论
考虑适筋梁截面受拉钢筋开始屈服及屈服之前和达到截面最大承载力时受压区高度的变化,得出简化损伤钢筋混凝土梁的刚度计算公式为:
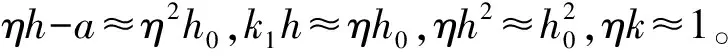
(13)
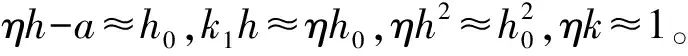
(14)
其中,K为对其他参数的综合考虑,记为
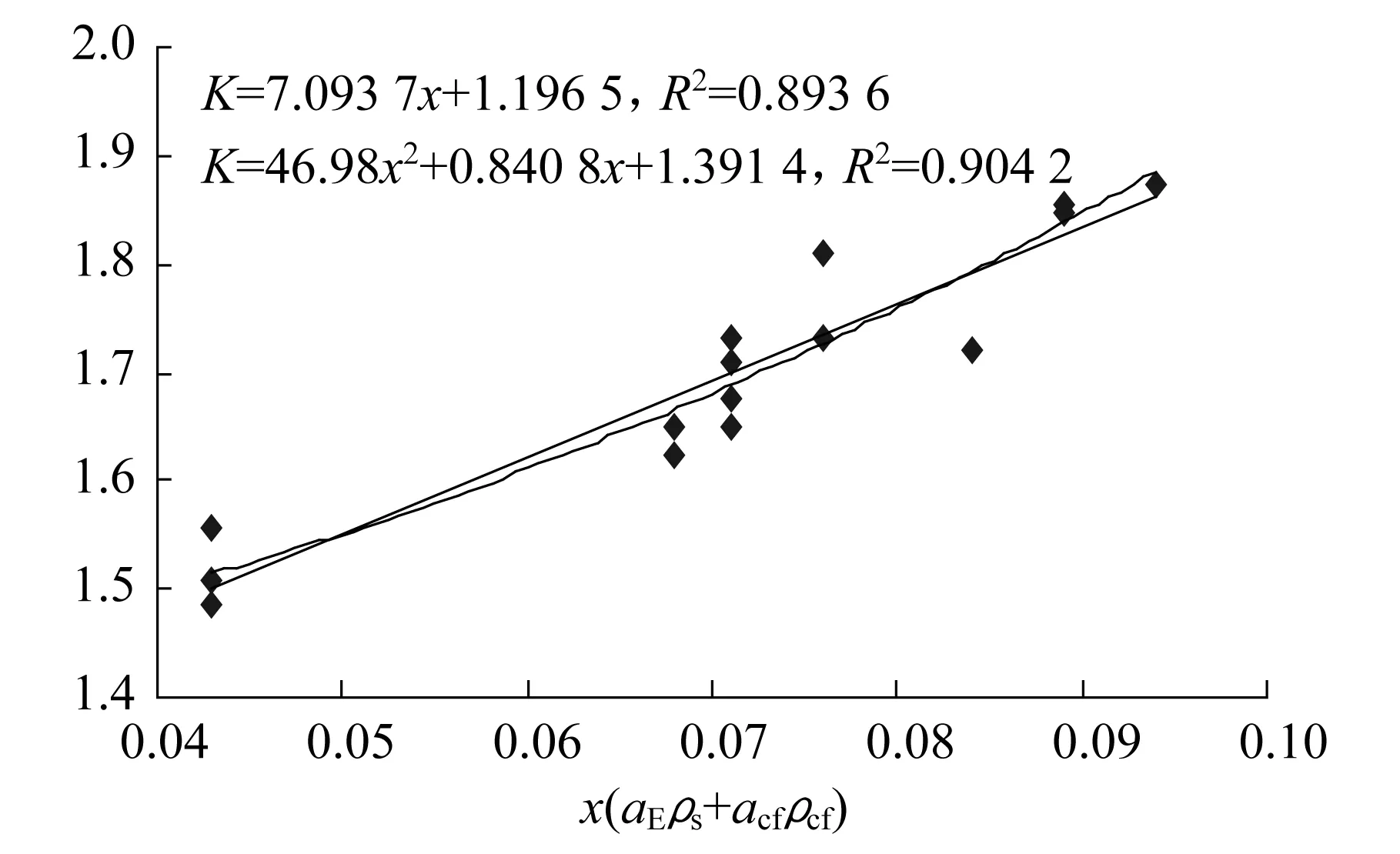
称为碳纤维布加固损伤混凝土梁截面刚度的综合变化系数,其中系数ξ=ηωλ(x0/h0)。根据分析K随着kk1aEρs+acfρcf的增大而逐渐增大,即K的数学表达式
3 系数的确定
3.1 钢筋初始应变的影响系数k
1) 若0≤Mi≤My时
由平衡条件式(7)得
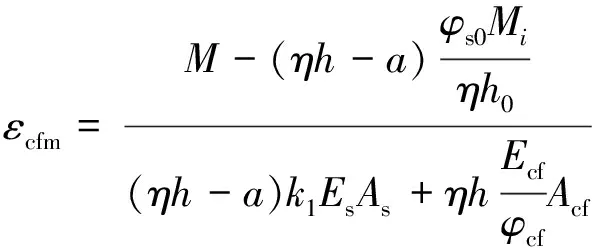
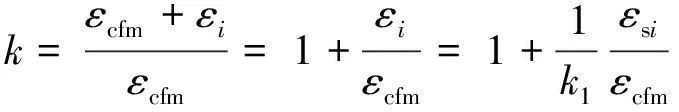
经整理得,
(1) 当不卸载加固时,
(2) 当卸载加固时,由于钢筋没有达到屈服,此时尚不考虑其残余变形。此时Mi=0,则k=1。
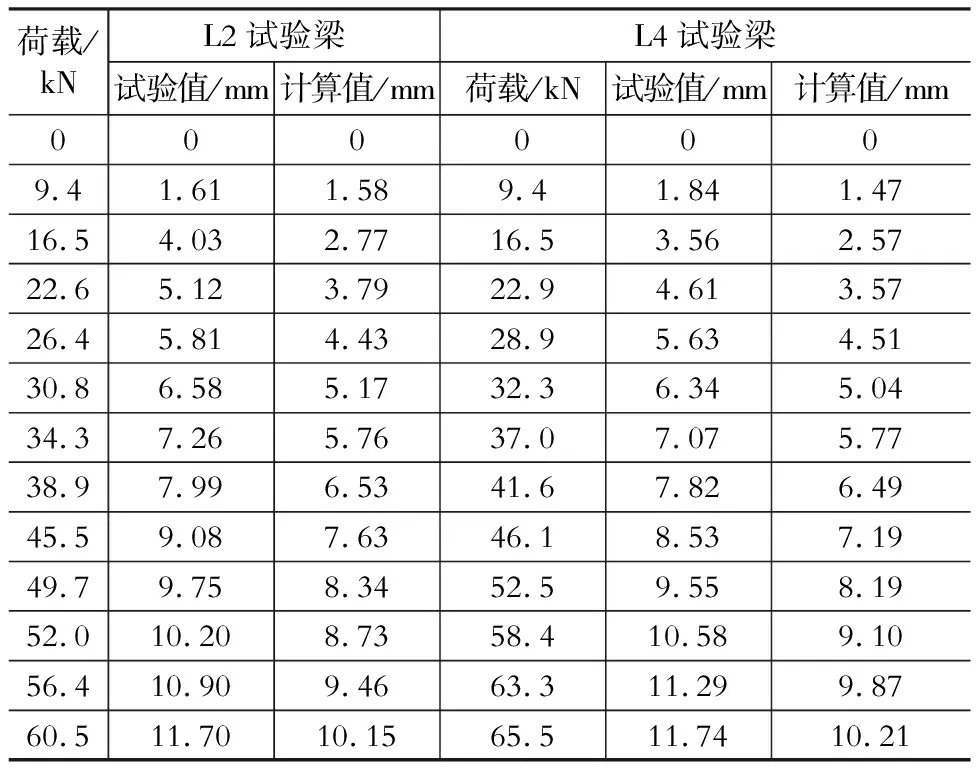
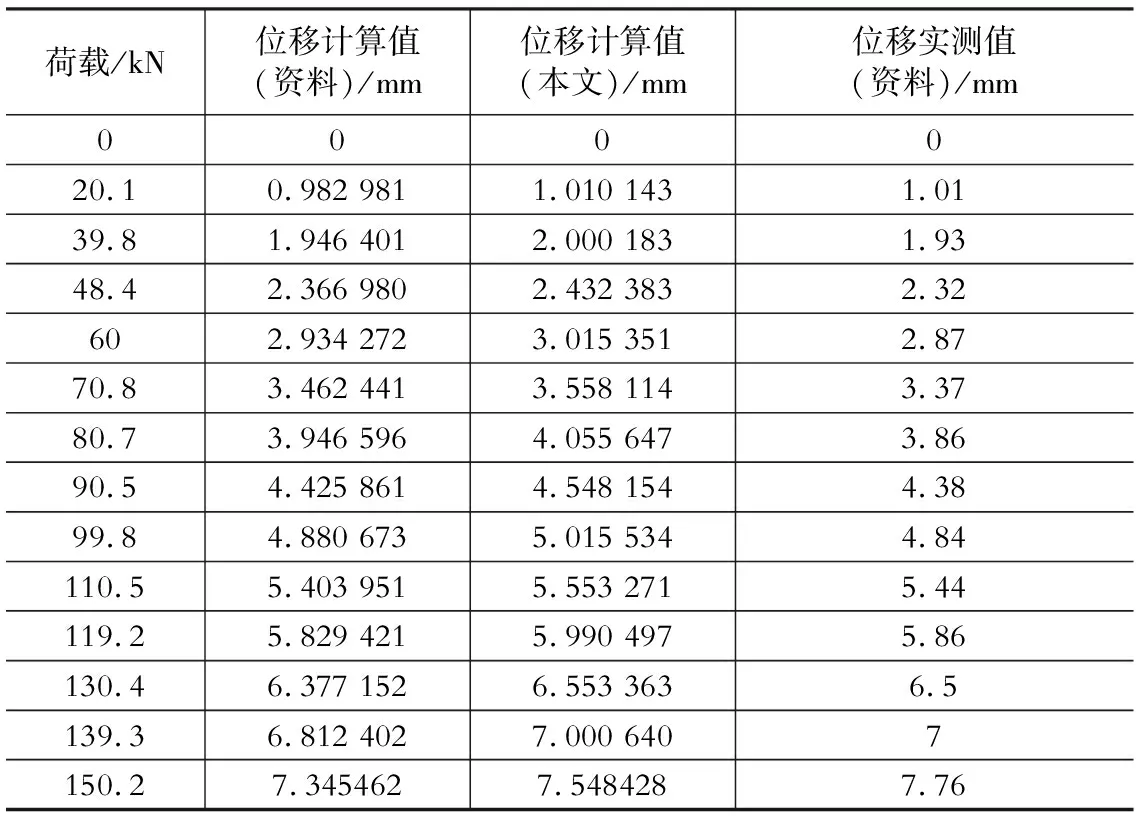
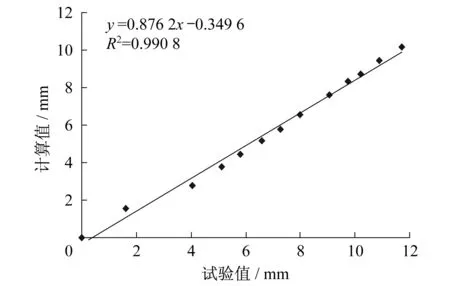
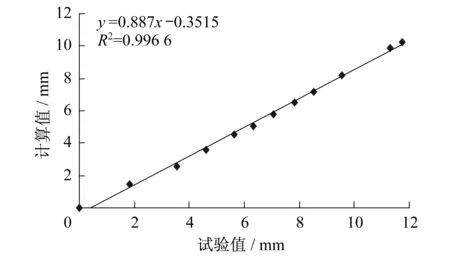
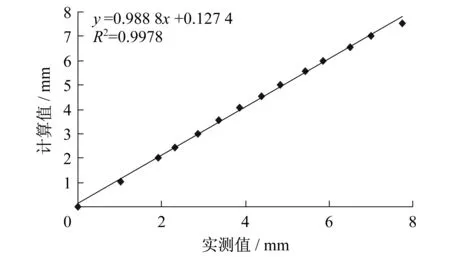
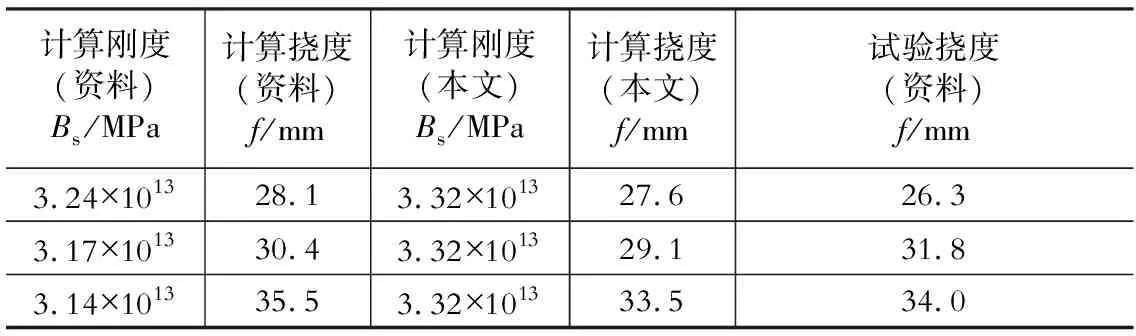
2) 若My 此时钢筋已进入屈服阶段,压区混凝土没有被压碎。 (1)当不卸载加固时,由平衡条件式(7)得 经整理得, (2) 当卸载加固时,由于此时钢筋已经屈服,要考虑卸载时钢筋的残余变形。假设钢筋屈服后卸载其屈服前的弹性变形仍能够恢复,受压区混凝土没有被压坏。 经整理得, 经整理得, ξ为受压区边缘混凝土平均应变综合系数。 6(k1aEρs+acfρcf/k)+0.2(k1+1/k) 式中:σsi,σss为短期荷载作用下钢筋、CFRP中的拉应力;Mu为CFRP加固损伤混凝土梁极限承载力。 K=6(k1aEρs+acfρcf/k)+0.2(k1+1/k)+1.15φcf 参照相关文献资料的试验结果[8,13-15],得到了在一般使用条件下K与aEρs+acfρcf的拟合关系,如图4所示,其统计线性表达式和统计二次项表达式分别为 本文为了简化取统计线性表达式来验证。 图4 截面刚度的综合变化系数K与aEρs+acfρcf的关系Fig.4 The relationship between the coefficient of variation of the section stiffness K and aEρs+acfρcf 对于0≤Mi≤My不卸载加固时,由本文给出的公式(13)计算的刚度值及其计算挠度值与所给出引相关资料[13]的对比如表1所示。按本文提出的公式计算的挠度值与实测挠度值比值的平均值为0.983 3,标准差为0.055。说明计算结果具有较高的精度。 表1本文理论计算值与资料理论计算值、试验值比较 Table 1 Theoretical calculations of this paper compared with theoretical calculations and experimental value of test data 对于0≤Mi≤My不卸载加固时,由本文给出的公式(13)计算的挠度值与所给出引相关资料[14]的对比如表2所示。按本文提出的公式计算的挠度值与实测挠度值比值的平均值为0.759,标准差为0.047。说明计算结果具有较高的精度。 表2挠度计算值与试验值比较 Table 2 Comparison between calculation and experimental values of deflection 参照相关资料的试验结果,对于0≤Mi≤My和My≤Mi 由表3、表4及图5-图7可以看出,采用本文提出公式的计算结果与试验值(实测值)比较接近,具有较高的精度,可用于碳纤维布加固损伤混凝土梁正常使用阶段的刚度计算。 表3挠度计算值与试验值比较 Table 3 Comparison between calculation and experimental value of deflection 表4理论计算值与资料理论计算值、试验值比较 Table 4 Theoretical calculations compared with theoretical calculations and experimental value of test data 图5 表3中L2试验梁跨中挠度试验值与计算值线性拟合图Fig.5 Linear fitting of the L2 beam midspan deflection test values Table 3 and calculated values 图6 表3中L4试验梁跨中挠度试验值与计算值线性拟合图Fig.6 Linear fitting of the L4 beam midspan deflection test values in Table 3 and calculated values 图7 表4中梁跨中挠度实测值与计算值线性拟合图Fig.7 Linear fitting of the beam midspan deflection test values in Table 4 and calculated values 本文对在正常使用阶段碳纤维布加固损伤混凝土梁的截面短期刚度进行解析分析,给出了在不同损伤即屈服弯矩之前和屈服弯矩至极限弯矩两种情况下,其截面短期刚度表达式。并基于试验资料分析提出用损伤混凝土梁截面刚度综合变化系数K表达各种因素对碳纤维布加固钢筋混凝土梁截面刚度的影响并进行拟合,给出加固损伤混凝土梁截面短期刚度的简化计算公式,且与资料试验结果比较表明,本文公式具有较高精度,可供参考。 鉴于相关试验资料有限,且混凝土强度等级大多数在C25~C30,试验数据相对不足。故损伤混凝土梁截面刚度的综合变化系数K还有待进一步修正和研究。
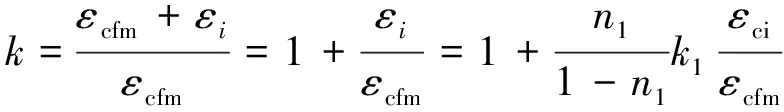
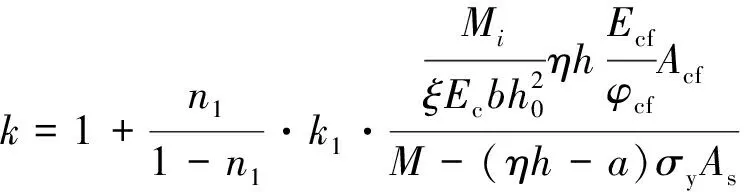

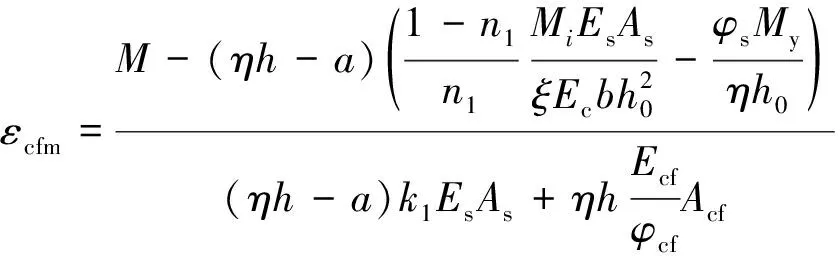
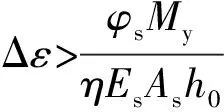

3.2 系数ξ
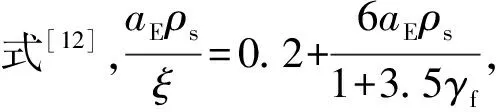
3.3 钢筋、碳纤维布应变不均匀系数φs,φcf
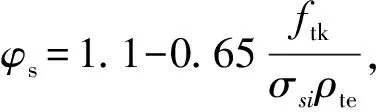
3.4 碳纤维布加固损伤混凝土梁截面刚度的综合变化系数K
4 试验验证
4.1 不卸载加固

4.2 卸载加固
5 结 论