底部内爆作用下钢框架的连续倒塌分析

2018-11-22谢丽萍于海丰郝红红陈世玺黄友强

结构工程师 2018年5期

谢丽萍于海丰郝红红陈世玺黄友强

(1.国核电力规划设计研究院有限公司,北京 100095; 2.河北科技大学建筑工程学院,石家庄 050018;3.河北拓朴建设设计有限公司,石家庄 050051)

0 引言

在国际恐怖主义事件中,炸弹袭击是非常普遍的方式,信件炸弹、背包炸弹、汽车炸弹等爆炸袭击事件时有发生[1]。爆炸事件不仅会对人身安全造成严重威胁,还会对建筑物造成影响使其部分构件破坏甚至结构整体倒塌。

目前,钢结构在我国发展迅猛。对于钢结构在爆炸荷载下的动力响应分析,国内外学者都已做了大量研究。Izzuddin和Fang[2-3]对爆炸荷载作用下钢材的本构关系和动力性能进行了分析。Nonaka[4]研究了钢材在爆炸作用下的破坏形态。谢甫哲等[5]对平面钢框架结构进行了抗倒塌动力试验研究并进行了数值分析。杜修力等[6]提出了可采用简化的分析方法来模拟爆炸荷载作用下的钢框架连续倒塌问题。张秀华等[7]分析了爆炸荷载大小、钢柱截面尺寸、钢柱高度等因素对钢柱动力响应的影响。李国强等[8]研究了爆炸作用下钢柱破坏时间及残余承载力对钢框架连续倒塌的影响。郑玉芳等[9]基于LS-DYNA建立了三层两跨钢框架结构模型,并对其在不同爆炸荷载工况下的倒塌情况进行分析,总结出了多层钢框架结构的倒塌规律。

迄今为止,学者对钢结构在爆炸作用下连续倒塌问题的研究大多集中在构件或小型无板的框架上。目前,国内规范[10]关于钢结构的抗连续倒塌则更侧重于概念设计,有特殊要求时才采用拆除构件方法。但发生爆炸事件时,直接因受爆炸荷载失效破坏的构件往往不止一个,且失效构件的数量和位置都是未知的。针对这一现状,本文建立了一个10层的空间钢框架结构模型,模型考虑了钢筋混凝土板的影响,比较贴合实际情况,划定了直接受爆区域,用直接施加偶然荷载法,研究了其连续倒塌问题,并给出可一些有益的结论。

1 模型信息

1.1 结构模型基本信息

设计出的10层钢框架模型平面图如图1所示,纵向8跨,横向4跨,跨度均为6 m,层高均为3.9 m。结构所受的荷载信息为:楼面承受,楼面做法及管线荷载按5 kN/m2计,活载按3 kN/m2计;边梁承受墙体线荷载按8kN/m计。假设结构处于抗震设防烈度6度区,不考虑地震荷载。设计时考虑的荷载组合有:①1.2D+1.4L;②1.35D+1.4×0.7L;D代表恒荷载,L代表活荷载。钢框架梁柱均刚接,柱脚固结。为简化分析,分析中不设置次梁。钢材选用Q345钢,楼面板选用钢筋混凝土板,混凝土选用C30,钢筋选用HRB400。各构件截面尺寸如表1所示。

1.2 有限元模型

有限元模型通过数值软件ABAQUS建立,如图2所示。由于模型较大,梁、柱构件采用B31梁单元构建,钢筋混凝土板选用可附加钢筋层的S4R壳单元构建,钢筋“Rebar Layer”命令添加,钢筋与混凝土之间的粘结力通过“tension stiffening”实现。梁与板采用共用节点连接。柱底约束三个方向的平动及转动。

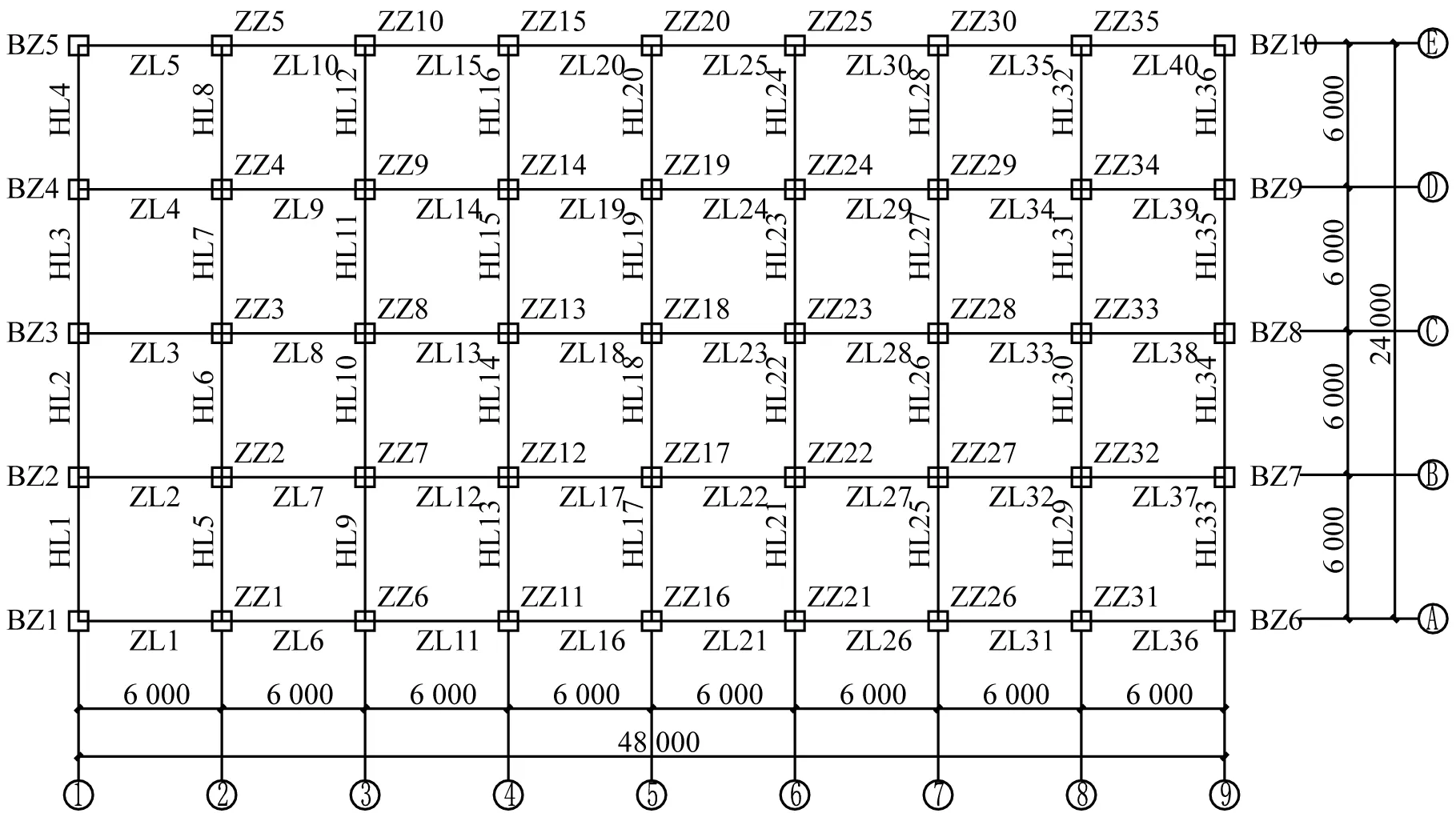
图1 钢框架结构平面布置图(单位:mm)Fig.1Plane layout of steel frame structure (Unit:mm)

表1构件截面尺寸

Table 1 Members sections

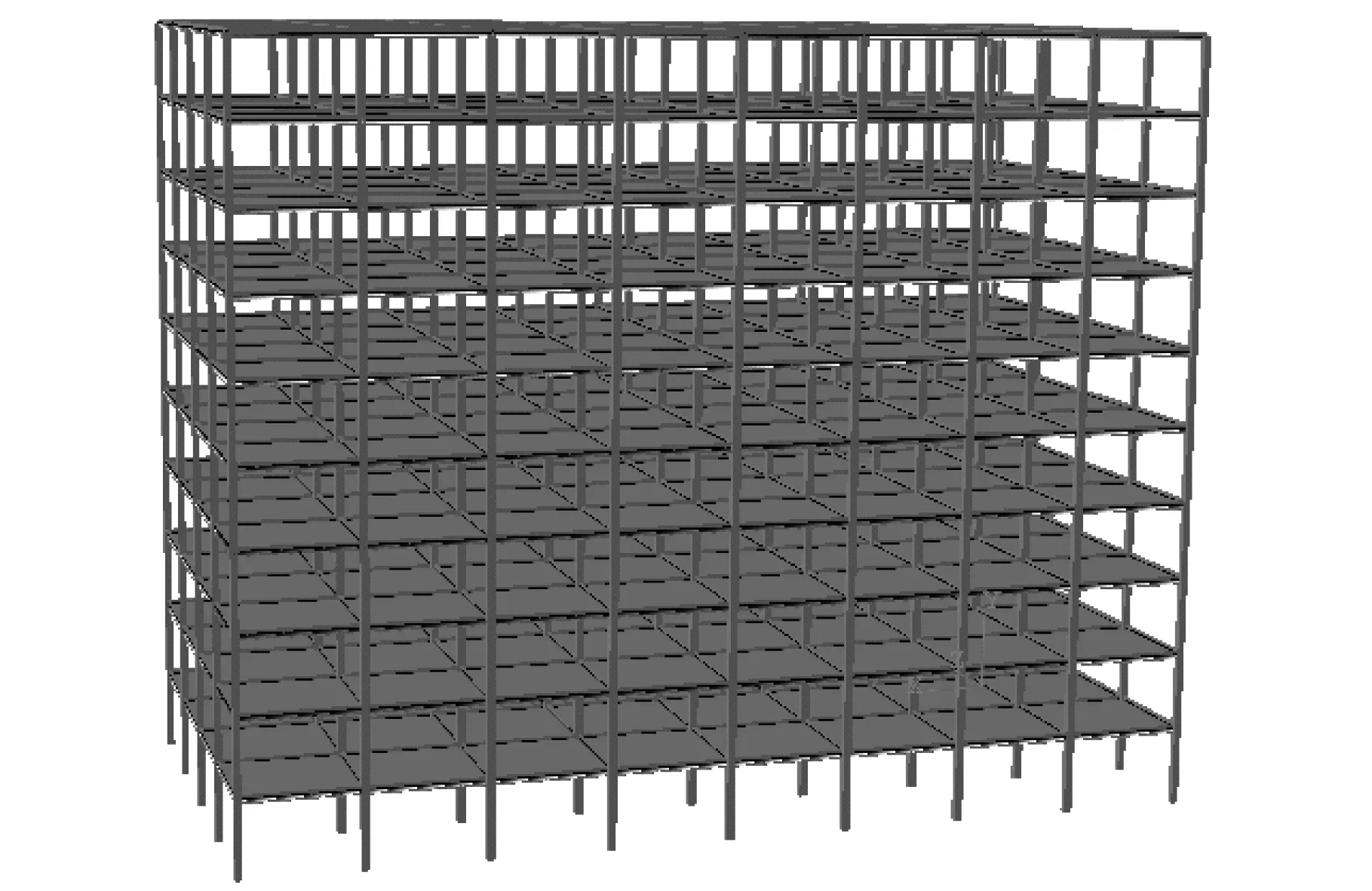
图2 钢框架有限元模型Fig.2 Finite element model of steel frame

1.3 材料定义

模型中的钢材选用修正的Johnson-Cook本构模型,Johnson-Cook本构模型是Johnson和Cook在1983年提出来的,模型采用关联流动法则的Von-Mises屈服准则,但是采用了不同的强化准则并且考虑了应变速率的影响,可以模拟爆炸冲击荷载作用下大多数金属的变形[11]。文献[12]研究表明,钢材在非接触性爆炸冲击荷载作用下,因爆炸冲击作用分析时间短暂,钢材在此过程中的升温一般不会高于200℃。当温度在室温-200 ℃范围内时,钢材的力学性能不会发生较大的变化,因此在分析时可不考虑温度软化的影响,经过修正的Johnson-Cook本构方程如式(1)所示:

(1)

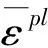
本文分析时上述系数分别取A=3.502 5×108,B=2.75×108,C=0.022,n=0.36。

与Johnson-Cook本构模型相对应的,ABAQUS/Explicit还提供Johnson-Cook动力失效模型来定义材料的失效过程,Johnson-Cook动力失效模型是基于单元整体积分点的等效塑性应变而确定的失效准则,当材料损伤参数ω>1时,材料失效破坏。

(2)

(3)

式中:d1,d2,d3,d4,d5代表材料损伤失效参数,本文分析时取值分别为-1.24、1.8、0.5、0.002、0.61;p代表静水压力;q代表Mises等效应力。

对于带有钢筋混凝土板的空间钢框架结构在爆炸冲击作用下的连续倒塌响应分析,尚需要钢筋和混凝土的力学模型。本文中钢筋是通过“Rebar Layer”附加到壳单元上的,此种方法建立的钢筋与混凝土的特性是独立的。钢筋选用Johnson-Cook本构模型,混凝土选用Brittle Crack本构模型,由于是C30混凝土,故破坏时的抗拉强度取为2.01 MPa,材料达到其抗拉强度时,抗剪切的能力保留因子为1,极限拉应变取0.000 1。Brittle Crack本构模型仅适用于ABAQUS/Explicit分析模块,模块中有相应的brittle failure破坏准则来去除失效构件,当材料点的一个局部开裂应变分量达到破坏应变值时,材料点发生破坏,该点所有的应力分量均置为零。如果壳单元沿厚度方向的所有材料点都破坏了,则将该单元从模型中移除[13]。

2 爆炸荷载

2.1 爆炸荷载的计算

爆炸是物质伴有物理或化学能量释放过程的物理反应或化学反应。按照爆炸的性质不同,爆炸可分为物理爆炸、化学爆炸和核爆炸[14]。本文以化学爆炸(TNT炸药)为主要研究对象。普通化学爆炸是短时间内化学能向机械能转化的过程,短时间内能量的迅速转化必然会对周围介质产生高压,形成冲击波。爆炸压力大于爆前周围大气的压力称为超压。科研人员以相似理论为基础,通过量纲分析和实验标定参数的方法得到了爆炸冲击波的超压峰值经验公式。

著名的爆炸超压经验公式有:Brode经验公式、Henrych经验公式、Miles经验公式。基于不同超压经验公式得到的折合距离Z与超压峰值ΔP的相关关系如图3所示。

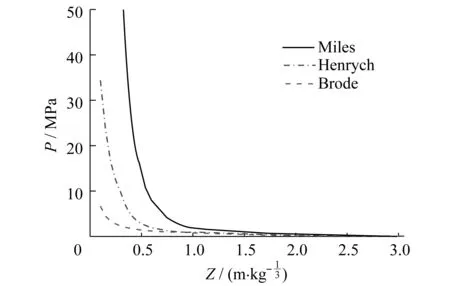
图3 超压经验公式Fig.3 Empirical formula of overpressure peak value

由图3可以看出:相同折算距离Z情况下,Miles超压经验公式计算的超压峰值ΔP最大,Brode超压经验公式果最小,Henrych居中。当Z<0.5 m/kg1/3时,三种超压经验公式计算结果差别很大;当Z>1 m/kg1/3时,三者计算结果越来越接近。因此,采用不同的爆炸超压经验公式得到的结果截然不同且可能差别很大。本文分析时,考虑到Henrych爆炸冲击波超压经验公式计算结果居中,且与美国TM5-1300手册中的计算结果比较接近[15],本文最终选用Henrych爆炸冲击波超压经验公式,具体如下:

0.1≤Z<0.3

(4)

0.3≤Z<1

(5)

1≤Z<10

(6)

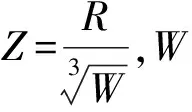
本文研究的是室内地面爆炸,可看作2倍的炸药量在无限空气中爆炸,将2W代入Henrych经验公式,计算得出爆炸冲击波超压峰值。爆炸冲击波的峰值特征标准时程曲线基于对气体扩散有限制的条件下发生爆炸时确定[16-17],如图4所示。

图4 对气体扩散有限制的典型超压时程曲线Fig.4 Diffusion curves of typical overpressure under limiting gas

2.2 爆炸荷载的施加

对于结构倒塌分析来说,首层一般是最不利爆炸荷载位置,所以本文仅研究爆炸荷载作用在钢框架结构底层室内地面不同部位所引起的倒塌问题分析。

假定发生在钢框架内部的爆炸荷载确定原则如下:爆炸距离R取构件上任意一点至爆心距离的最小值,即楼板和墙面上任一点至爆心的最小距离。根据此爆炸距离计算出作用在楼板和墙面上的超压峰值。基于双向板荷载传递理论,将作用在楼板上的荷载传递到与之相连的梁上,作用在墙面上的荷载传递到墙两端面支承的柱子上,爆炸荷载传递形式如图5所示[18]。

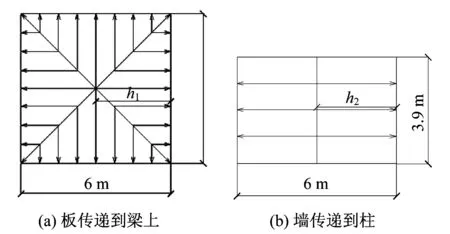
图5 爆炸荷载传递路径图Fig.5 Transmission path diagram of explosion load

2.3 载荷时间曲线

本文规定楼面做法及管线荷载,自重,活荷载统称为常载。ABAQUS/Explicit显示动力分析的时间增量非常短,如果分析时间过长,计算量会非常大,本文只计算4 s,分析时只取1～3 s之间的结果。因为只有一个分析步,所以将常载在前1 s施加到结构上,由于常载施加时间较长,可将前1 s看作静态分析,在1 s过后再施加爆炸荷载。

3 钢框架连续性倒塌分析

3.1 直接受爆区的划定与爆炸荷载工况

本文定义直接受爆区为炸药所在密闭房间范围,本节房间布置为两个开间为一个封闭房间。根据考虑的炸药不同位置,直接受爆区范围为图6中虚线框框选范围。直接受爆区爆炸荷载等效计算简图如图7所示。

图6 爆炸荷载位置示意图(单位:mm)Fig.6 Schematic diagram of explosive load position (Unit:mm)

根据炸药量的大小将爆炸荷载分为4个大工况,再根据图6所示的爆炸作用位置将爆炸荷载分为20个小工况,具体工况详见表2。

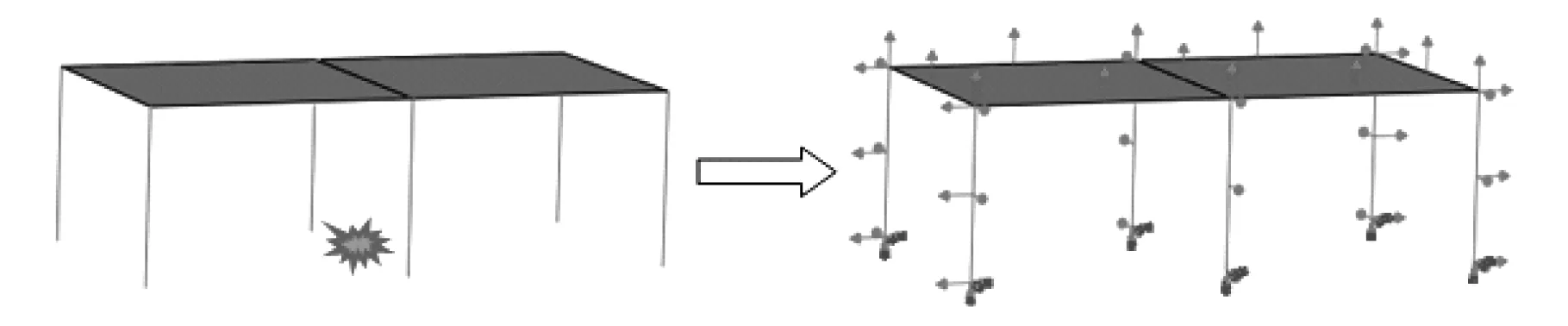
图7 爆炸荷载等效计算简图Fig.7 Equivalent calculation diagram of explosion load

表2爆炸荷载工况

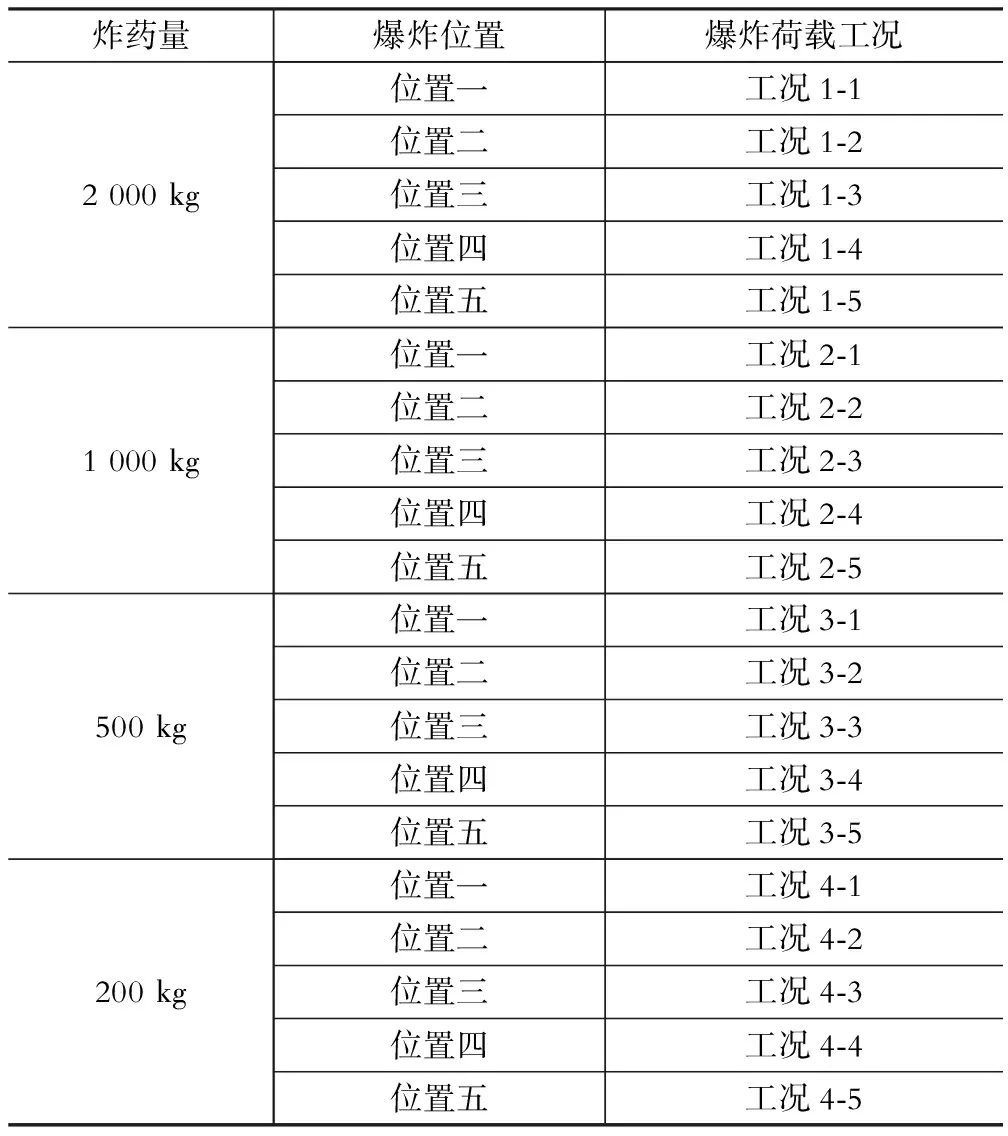
Table 2 Explosion load condition

3.2 计算结果

3.2.1爆炸荷载作用在位置一处时

爆炸荷载作用在位置一处(工况1-1、工况2-1、工况3-1、工况4-1)时,直接受爆区范围的柱子、梁和板都发生了失效破坏,直接受爆区正上方的位于结构二层的部分柱子也发生失效破坏,直接受爆区周围一跨的板发生了局部破坏。工况1-1作用下,钢框架结构的应力及整体变形情况如图8所示,其他三种工况作用下钢框架的变形情况与工况1-1类似,不再给出。

直接受爆区范围柱ZZ11、ZZ16(图6)第二层顶节点以及非直接受爆区范围柱ZZ6、ZZ7(图6)首层顶节点的竖向位移响应见图9,可见:

图8 工况1-1时钢框架应力云图Fig.8 Stress diagram of steel frame under condition 1-1

(1) 直接受爆区上方构件节点的竖向位移在这四种工况作用下都很大。3 s时ZZ11柱顶节点的竖向位移在工况1-1作用下最大,达到了-2.669 m,在工况2-1作用下最小,约-2.526 m;ZZ16柱顶节点的竖向位移在工况2-1作用下最大,达到了-2.656 m,在工况4-1作用下最小,约-2.575 m。表明在位置一处爆炸时,直接受爆区上方部位发生了倒塌,而且并非是炸药量越多,位移响应越大。

(2) 非直接受爆区的位移响应比直接受爆区位移响应小得多,在3 s时:ZZ6柱顶节点竖向位移在工况3-1作用下最大,约-0.051 m,在工况2-1作用下最小,约-0.046 m;ZZ7柱顶节点竖向位移在工况3-1作用下最大,约-0.077 m,在工况1-1作用下最小,约-0.061 m。表明爆炸荷载对钢框架结构的影响具有局部性和弱传递性。

分析结构倒塌原因可知,爆炸荷载作用于梁、柱后,柱破坏导致受爆区结构失去了竖向的直接传力途径,进而直接受爆区结构产生较大竖向位移,同时,本该由破坏的柱承担的荷载通过梁、板传递至剩余结构上,进而与直接受爆区相连的非直接受爆区结构柱产生较大位移,甚至引发进一步的结构倒塌。通过逐步传递,离受爆区越远的构件破坏程度越轻。

结合图8、图9可看出:在这四种工况下③-⑦轴与A-C轴之间的结构发生倒塌,倒塌面积占结构总面积的25%左右,并且炸药量为200～2 000 kg在位置一处发生爆炸引起的结构倒塌情况基本一样。

3.2.2爆炸荷载作用在位置二处时

在(工况1-2、工况2-2、工况3-2、工况4-2)这四种工况下,直接受爆区内柱BZ1、ZZ1、BZ2先于ZZ2、ZZ6、ZZ7破坏,破坏时间在1.36～1.38 s之间,其中工况3-2作用下最早。表明爆炸荷载作用下边角部位构件受到的影响较大。除上述各柱外,紧接着破坏的是柱ZZ3和ZZ11,其破坏时间在2.06～2.12 s之间。在3 s时,远离直接受爆区的位于顶层的BZ10柱顶节点竖向位移也达到了-0.688 m (工况1-2)、-0.639 m (工况2-2)、-0.747 m (工况3-2)、-0.691 m (工况4-2),而且其位移时程曲线呈下降趋势并无收敛迹象,表明在这四种工况作用下钢框架结构最终发生整体倒塌。3 s时,工况1-2作用下钢框架整体应力及变形示意图如图10所示。

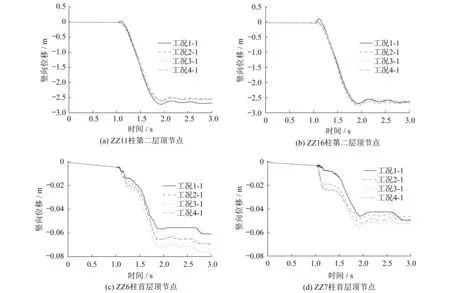
图9 爆炸荷载作用在位置一处各柱位移响应Fig.9 Column deformation response of steel frame when blast load at location 1

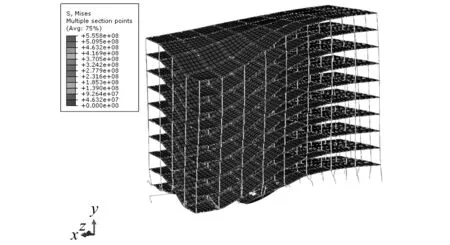
图10 工况1-2时钢框架应力云图Fig.10 Stress diagram of steel frame under condition 1-2

3.2.3爆炸荷载作用在位置三处时

在(工况1-3、工况2-3、工况3-3、工况4-3)这四种工况下,直接受爆区内柱BZ5、ZZ5、BZ4先于柱BZ3、ZZ4、ZZ3破坏,破坏时间在1.36～1.40 s之间,其中工况1-3、2-3作用下最早。除上述各柱外,紧接着破坏的是直接受爆区旁边区域内BZ2、ZZ2,破坏时间在1.94～2.00 s之间,明显先于其他柱子倒塌,BZ2的倒塌时间在工况2-3、3-3、1-3作用下相差不多,在1.94 s左右开始倒塌;其次是工况4-3作用下,在2.0 s左右开始倒塌。然而对于直接受爆区旁边区域整体而言,在工况2-3作用下的位移响应最大,在工况1-3作用下的位移响应最小。

3 s时,工况1-3作用下钢框架结构应力及整体变形如图11所示,此时远离直接受爆区的位于顶层的BZ10柱顶节点竖向位移为-0.104 m (工况1-3)、-0.790 m (工况2-3)、-0.559 m (工况3-3)、-0.148 m (工况4-3),并且其位移时程曲线呈下降趋势并无收敛迹象,表明在这四种工况作用下钢框架结构最终发生整体倒塌。

3.2.4爆炸荷载作用在位置四处时

在(工况1-4、工况2-4、工况3-4、工况4-4)这四种工况下,分析结束时直接受爆区及周围一跨部分结构向下坍塌了1.2 m左右,③-⑦轴与B-E轴之间部分结构倒塌,倒塌面积约占结构总面积的37.5%。工况1-4作用下的钢框架结构应力及整体变形如图11所示,其他三种工况下的整体变形与之类似。

图11 工况1-3时钢框架应力云图Fig.11 Stress diagram of steel frame under condition 1-3

分析发现,ZZ19的柱顶竖向位移是直接受爆区中ZZ13、ZZ14、ZZ18、ZZ19、ZZ23、ZZ24这6个柱子中最大的。ZZ19柱二层顶节点竖向位移达到了-1.251 m (工况1-4)、-1.129 m (工况2-4)、-1.222 m (工况3-4)、-1.192 m (工况4-4),这也表明直接受爆区上方构件节点的竖向位移响应并不是随炸药量的增多而加大的。除上述各柱外,非直接受爆炸区柱ZZ20是竖向位移响应最大的,在3 s时首层ZZ20柱顶节点竖向位移为-0.027 m (工况1-4)、-0.028 m (工况2-4)、-0.031 m (工况3-4)、-0.047 m (工况4-4),但上述位移远小于直接受爆区的柱。

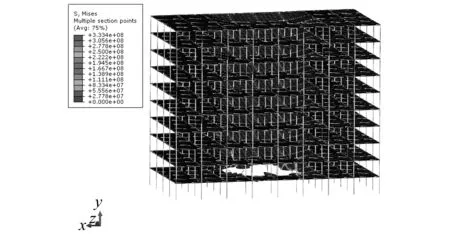
图12 工况1-4时钢框架应力云图Fig.12 Stress diagram of steel frame under condition 1-4

3.2.5爆炸荷载作用在位置五处时

在(工况1-5、工况2-5、工况3-5、工况4-5)这四种工况下,直接受爆区内柱BZ7、BZ8、BZ9先于柱ZZ32、ZZ33、ZZ34破坏,破坏时间在1.40～1.46 s之间,其中工况1-5作用下最早。

直接受爆区旁边区域各柱顶节点的位移响应差别很大,但都呈现出共同规律,即工况2-5>工况1-5>工况4-5>工况3-5。比如3 s时,首层ZZ26柱顶节点的竖向位移为-0.766 m (工况1-5)、-1.582 m (工况2-5)、-0.029 m(工况3-5)、-0.336 m (工况4-5)。

3 s时,远离受爆区的十层BZ1柱顶节点竖向位移均较小,最大也仅在0.022 m (工况3-5),但是在分析时间段内并没有收敛的迹象,故无法判断其是否发生整体倒塌。在此仅根据分析时段内钢框架结构的变形情况来判断其倒塌范围,3 s时,工况1-5作用下钢框架结构应力及整体变形如图13所示(因篇幅所限,其余工况未给出),经判断知,工况1-5和工况2-5作用下钢框架结构有37.5%发生了倒塌,倒塌范围为⑥-⑨轴与A-E轴之间部分。在工况3-5和工况4-5作用下钢框架结构有25%发生倒塌,倒塌范围为⑦-⑨轴与A-E轴之间部分。