莱比塘铜矿特高品位的识别与处理方法研究

李 健， 任 太 平， 黄 晓 华， 赵 天 雷

(中国水利水电第十工程局有限公司，四川 都江堰 611830)

1 概 述

蒙育瓦莱比塘(Letpadaung)铜矿系特大型露天铜矿，位于缅甸联邦共和国西北部实皆省(Sagaing)南部，简称L矿。L 矿位于两山包及中间沟谷之下，为隐伏矿床，整体呈一个顶面平整的金元宝型，走向NW，走向长约2 200 m，宽约1 400 m，产状基本水平。矿体平均厚度约143 m，平均品位为0.37%。L矿Cu边际品位为0.1%。

目前，该项目已进入生产采剥期，在实际生产过程中，爆区圈定的矿体平均品位对采矿生产和选矿工作起到了重要的指导作用，是控制矿石贫化率和损失率的重要依据。在计算平均品位时，常出现特异的极值品位。这种极值品位若处理不当，常常会影响到爆区平均品位的计算结果，因此，对爆区特高品位处理方法进行研究很有必要。对特高品位的识别与处理方法研究进行了阐述。

2 爆区极值品位的识别与处理

“由于矿石组分的不均匀性和取样方法、取样手段及取样主体的偶然性，在样品采集过程中偶尔会出现个别样品的品位值比全部样品的算术平均值高得多的品位，称之为特高品位”[1]。但是，忽视这些特高品位的样品是不恰当的。虽然其在全部样品值中只占少部分，但它对爆区平均品位值的统计结果影响较大。倘若将特高品位不经处理即直接用于爆区平均品位的计算，尤其在样品数较少时，将会导致高估金属量，进而为后续浸出率的计算带来较大的误差。因此，有必要对极值品位的样品处理进行系统的研究。

特高品位的处理方法主要有剔除法和替代法。但为了不损失信息量，不能简单地使用剔除法将特高品位直接剔除，采用更多的方法是用固定的上限值代替特高品位值。

2.1 目前采用的识别与处理方法

“处理特高品位值常用的方法主要有传统方法、经典数理统计法、地质统计学法等。传统方法主要为经验类比法，其根据矿床类型与矿石品位变化特点，将品位值高于爆区品位算术平均值5～12倍的值定为特高品位，当爆区内品位变化系数大时取上限值；当爆区内品位变化系数小时取下限值。经典数理统计法主要依据样品均值、3倍标准差、变异系数以及分布密度函数曲线上拐点值识别和处理特高品位值。地质统计学法主要包括估计邻域法和影响系数法”[2]。

目前莱比塘铜矿项目采用传统方法确定特高品位下限值，用经验法取高于整个莱比塘平均品位(0.4%)的10倍(4%)为特高品位的下限值。处理特高品位的方法是用确定的特高品位(4%)下限值代替特高品位。

传统方法主要是根据人为的经验识别和处理特高品位，其结果因人而异，这种方法相对简单，在莱比塘项目的运用也一直被业主所认可。由于有几条大的构造带穿过莱比塘矿体，矿体品位受构造和蚀变影响比较明显，因此，爆区在不同区域品位变化比较明显。“在低品位爆区运用传统方法相对比较实用，但是在高品位爆区简单使用这种方法所取得的计算结果就有待研究”[3]。在莱比塘矿目前开采境界内的L15 m、L30 m台阶北部以及L15 m到L30 m南部已经出现部分爆区硅化特别明显的情况，其黏土含量很低。铜品位特别高的爆区，如L30-1110爆区，在该爆区采用传统方法处理特高品位，发现有12个特高品位，用4%代替后得到的平均品位值为1.39%，其计算结果明显偏低。

2.2 采用影响系数法处理特高品位

最终采用GL代替特高品位值”[4]。

利用影响系数法处理L30-1110爆区数据，将影响系数k设为5%时，得出爆区的平均品位为1.55%，且未发现特高品位。由此可以看出：该爆区整体品位偏高且没有影响整个爆区平均品位5%以上的单孔品位；如果仍采用传统特高品位处理方法会造成整个爆区的平均品位值比理论品位值偏低，因此，使用传统方法处理极值品位不完全适合于所有爆区平均品位值的计算，而影响系数法可以比较科学的处理爆区极值品位，从而得到更接近爆区理论品位值的平均品位值。

影响系数法不适合数据量很多的情况。因为影响系数法需要经过多次扫描才能识别与处理特高品位。根据影响系数法的原理，影响系数法在使用前需要确定影响系数k值，而不同的k值得到的结果亦会不同。为了更加科学的对k值进行选取，需做专门的研究。

2.3 影响系数法k值的选取

对于使用影响系数法进行特高品位的识别和处理，影响系数k值如何选取一直是业内争论的话题。为了解决k值的选取，本次研究以莱比塘铜矿20个爆区的数据作研究样本进行研究。基于影响系数法，对不同爆区代入k值进行试算求取爆区平均品位值，其中k值的取值范围为0.01～0.14，将不同的k值在各个爆区对爆区平均品位的影响绘制成以k值为横坐标、平均品位为纵坐标的平均品位曲线图(图1)。

图1 平均品位曲线图

对比分析图1中各个爆区不同k值对爆区平均品位的影响曲线后可以看出：

(1)当0.01≤k<0.06时，绝大部分爆区的品位曲线变化较快，平均品位变化较大。说明k值取在该范围时，爆区的大部分炮孔品位值被当作了特高品位处理，使爆区平均品位大大降低，这一点明显不符合特高品位的处理规则。因此，对于爆区特高品位的处理，k值不能小于0.06。

(2)当0.06≤k≤0.1时，大部分爆区品位曲线趋于平缓，平均品位变化不大，仅有少部分爆区品位曲线仍有上升，平均品位有变化。说明k值取在该范围时，大部分爆区没有特异值，不需要做特高品位处理，仅有少量爆区存在特异值，需要做特高品位处理。这种情况符合处理特高品位的规则。上述现象在k=0.06时表现的尤为明显，且矿石品位偏差为2.1%，可以认为k=0.06比较适合莱比塘铜矿的实际情况。

(3)当k>0.1时，仅有极少部分爆区品位曲线有小幅度波动，平均品位基本无变化。说明除极少量爆区的炮孔需要做特高品位处理外，基本爆区不存在有特高品位的炮孔，这显然不符合实际情况。例如：在L-15-3076爆区中，当k>0.1时，该爆区无特高品位值，故不需要做特高品位处理；当k≤0.1时，该爆区需做特高品位处理。但是，该爆区单孔品位出现的7.13%明显属于特高品位值，需要进行处理。因此，当k>0.1时，可能会造成对部分爆区特高品位值的漏处理，从而给平均品位的计算带来较大误差。

2.4 3σ准则方法验证k=0.06的可取性

为了验证k=0.06的实用性，本次研究通过3σ准则方法加以验证。“3σ准则方法是一种特高品位处理的方法，它是以爆区平均值加上三倍均方差为特高品位下限值，大于该值的定为特高品位，然后用最大正常值替代特高品位”[5]。通过计算求得的20个爆区平均品位和偏差见表1。

表1 不同方法处理后各爆区平均品位和偏差表

在对比了3σ准则方法处理特高品位和影响系数法处理特高品位后的平均品位，发现在平均品位较高的爆区，两种方法处理后的平均品位绝对偏差较大：平均品位较低的爆区，两种方法处理后的平均品位绝对偏差较小。但通过对相对偏差的计算可以看出，两种方法得到的平均品位值相对偏差不大，基本都控制在5%以内，只有L-45-3017相对偏差为6.52%。通过分析L-45-3017的原始数据得知，该爆区特高品位比普通品位高出约10倍，采用3σ准则和影响系数法的代替值后其有所差别。影响系数法的代替值为0.67，3σ准则的代替值为1.22，二者相差约50%。

将表1中通过两种不同方法处理特高品位后的平均品位值数据转化为图形显示(图2)。使用影响系数法，选取k=0.06时，各个爆区进行特高品位处理后的曲线与使用3σ准则方法处理特高品位后的曲线基本吻合，从而验证了影响系数法在莱比塘铜矿特高品位处理中的可行性与科学性。通过影响系数法处理特高品位后得出的平均品位更接近爆区平均品位真值。故选取k=0.06比较符合莱比塘矿山的实际情况。

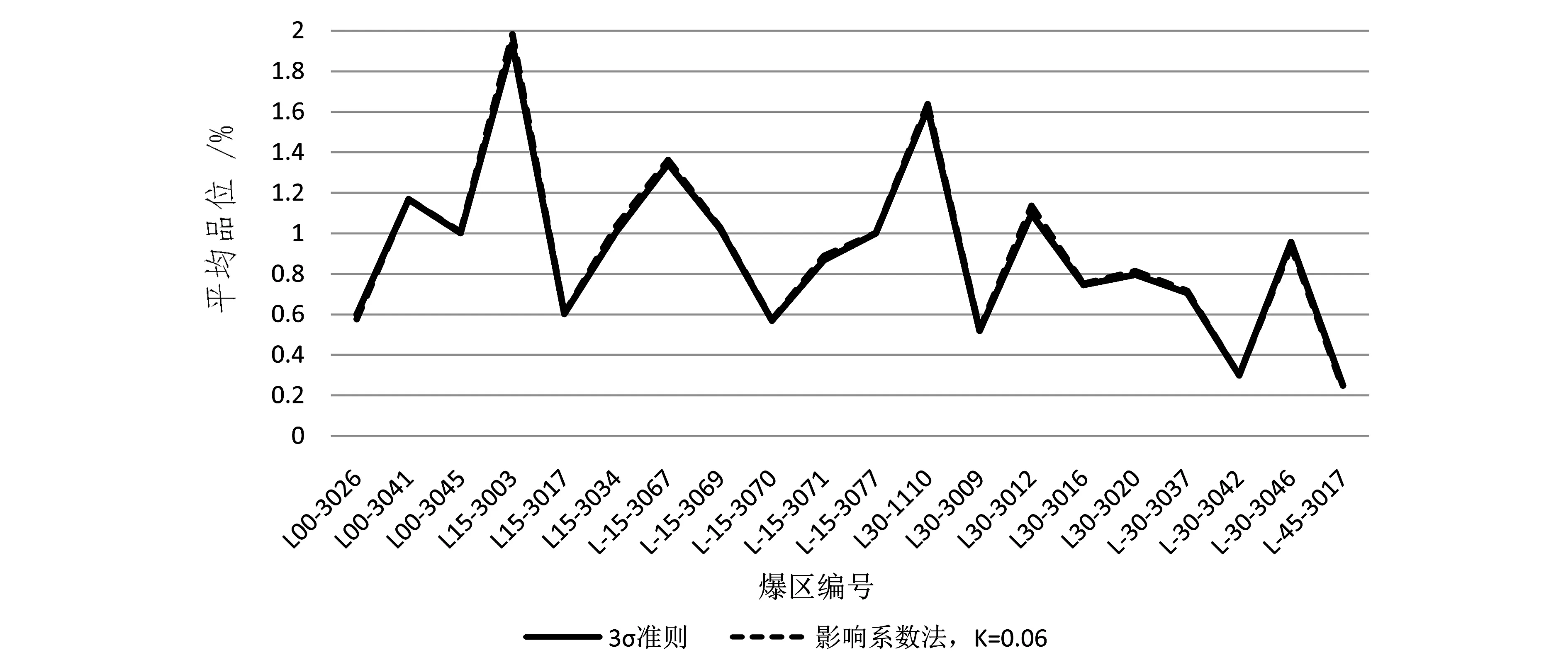
图2 不同方法处理特高品位后的平均品位对比图

3 结 语

通过研究，得到了以下结论：

(1)在矿体品位受构造和蚀变影响比较明显的区域，采用传统方法确定的特高品位值，其计算结果明显偏低。

(2)当k<0.06时，大部分炮孔的品位将被识别为特高品位并进行处理，从而违背了特高品位的特点，故k值不能小于0.06。当k>0.1时，将会出现爆区特高品位值的漏处理，从而给平均品位的计算带来较大误差。当0.06≤k≤0.1时，大部分爆区显示无特异值，不需要做特高品位处理，仅有少量爆区存在特异值需要做特高品位处理，这一点符合处理特高品位的规则。

(3)通过3σ准则方法加以验证，影响系数法可以比较科学地处理爆区极值品位，从而得到最接近爆区理论品位值的平均品位值。可以认为：取k值为0.06，比较符合莱比塘矿山目前的情况。