资产证券化对银行动机扭曲影响的实证分析

杨 默，张晓岚,2

（1.西安交通大学 经济与金融学院，西安 710061；2.上海对外经贸大学 会计学院，上海 201620）

0 引言

随着中国金融改革的不断深化，资产证券化在中国金融体制改革中的作用凸显。从资产证券化的试点开始，到发行审批制改为备案制，以及近年来稳步扩大银行资产证券化试点参与机构范围，中国资产证券化的规模和类型均取得突破性发展。对银行来说，特别是在推进利率市场化的背景下，资产证券化改变了传统商业银行发放贷款业务的方式。

传统观点认为资产证券化能为市场的不同参与方带来利益，能提高金融体系效率，增进社会福利[1-3]。在国外成熟的资本市场资产证券化已得到较快的发展，有足够的相关证券化案例和交易数据。我国资产证券化起步较晚，而且品种单一，产品主要集中在信贷资产证券化方面。但近年来得到快速的发展，目前已有的交易数据，不管在数量上还是质量上，均可以展开一定程度上的实证研究[4，5]。有关资产证券化的实证分析方面研究进展较快。巴曙松（2013）[6]、李佳（2015）[7]实证研究了商业银行资产证券化业务开展，能否降低成本，增加利润，提高银行的抗风险能力。高保中（2010）[8]、郭桂霞（2014）[9]利用商业银行的财务数据来研究资产证券化对于银行个体以及对银行系统风险传染的冲击影响，不过定性描述过多，定量研究不足。倪志凌（2011）[10]对资产证券化影响银行风险传染途径进行了深入研究，推断出资产证券化提高了银行资产流动性是银行系统风险传染的一个重要途径。从已有的文献来看，国内深入的实证研究较少，多数也是利用国外的数据。因此，本文采用国内商业银行数据，从流动性视角构建面板数据模型，来探讨资产证券化对银行动机扭曲的影响。

1 研究设计

1.1 变量的选取

本文被解释变量是商业银行的风险承受水平，根据已有文献，可用银行风险调整资产占总资产的比率来测度风险承受水平[10]，这一指标简写为RB。

对于解释变量，本文选取流动资产比率、证券化贷款比率、资产支持证券的利差三个变量作为解释变量，分别简写为LIAR、SLR、ILLI。选择证券化贷款比率作为解释变量是因为证券化贷款比率越高，银行就将越多的贷款进行了证券化，相应转移了更多的信用风险到银行的资产负债表之外。选取资产支持证券的利差作为解释变量来衡量市场的流动性状况，是因为资产的流动性状况可能对银行的风险承担水平造成影响，市场的流动性状况也可能对银行的风险承担水平造成影响。

对控制变量的选择，本文采用了可决系数决定法。通过处理，选取风险资本比率和坏账费用比率作为控制变量，分别简写为RCR和ALR。

1.2 模型的构建

由于样本数据的特点，本文采用面板数据模型进行分析。面板数据模型通常可以表示为：

式（1）中αi表示第i个个体的截距项，βi为解释变量Xit的系数，uit是动态随机误差项，满足正态分布。K为解释变量的个数。选择不同αi和βi值，模型可以分为三种不同类型：

（1）无个体影响的不变系数模型。即αi=αj和βi=βj同时得到满足。

（2）变截距模型。即是αi≠αj并且βi=βj。

（3）变系数模型。即满足αi≠αj并且βi≠βj。满足这一条件的模型称之为变系数模型或无约束模型。

根据对本文变量的分析，对式（1）方程展开并具体化，相应方程的表达式为：

随机效应估计模型：

RBit=β1LIARit+β2SLRit+β3ILLIit+β4RCRit+β5ALRit+b+μi+uit

固定效应估计模型：

RBit=β1LIARit+β2SLRit+β3ILLIit+β4RCRit+β5ALRit+ci+uit

混合二乘估计模型：

RBit=β1LIARit+β2SLRit+β3ILLIit+β4RCRit+β5ALRit+b+uit

在三种模型方程中，各变量的下标i表示不同的商业银行，各变量下标t代表时间，时间长度为季度。μi是满足任意分布的动态随机变量，ci是常数项，uit是残差项，满足动态分布。

1.3 样本数据的选择与处理

本文选取的样本主要是国内商业银行季度资产证券化数据和银行季度财务数据，数据来源于Wind咨询。选取样本数据的时间跨度为2010年一季度到2015年二季度。本文对季度数据进行了适当的处理，从中剔除了季度数据严重缺失的公司，以及在样本期间证券化程度太低的公司，最后梳理得到了46家银行控股公司的完整季度财务数据。

在建立面板数据模型之前，为了避免出现伪回归，首先对数据进行面板数据单位根检验。通过逐一对总体样本进行单位根检验。从分析的结果来看，在1%的置信水平上，被解释变量、解释变量和控制变量拒绝了存在单位根的假设，选择变量满足回归模型要求的平稳性条件。

本文将总体样本按资产规模分为两个子样本，一是资产规模较大，包括23家银行；二是资产规模较小，包括23家银行。从两个子样本的检验结果分析，绝大多数变量在1%的置信水平下是平稳的，所有变量在10%的置信水平下都是平稳的，因此可以假定子样本的所有变量也都是平稳的。

2 实证分析

2.1 总体样本的实证结果

由于面板模型的特点，在实证之前需要对数据进行分析，判断是否满足模型的要求。表1是对相关变量进行描述性统计分析的结果。表2是采用三种面板模型拟合的结果。

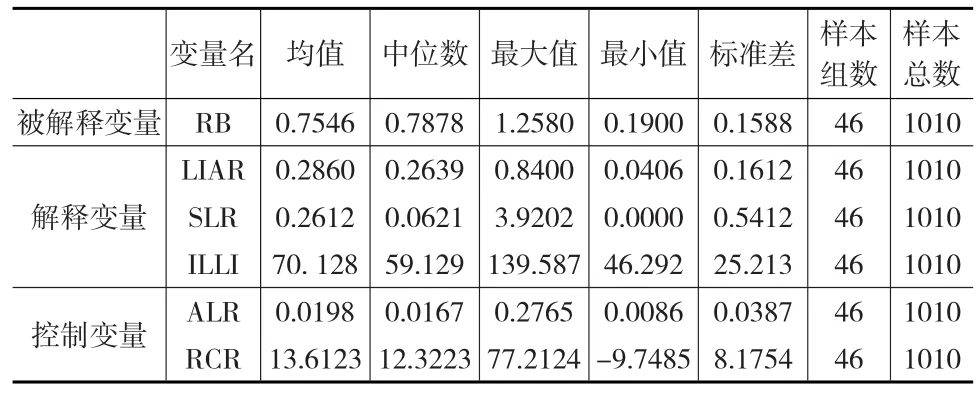
表1 样本数据统计

本文在选择模型之前，首先使用了假设检验“Redundant Fixed Effect”和“Hausman”进行检验。Hausman随机效应检验结果显著，概率p取值为1，也就表明随机效应模型相对于固定效应模型更适用，Redundant固定效应检验的p值为0。证券化贷款比率（SLR值）的拟合估计系数为0.018883，正相关，和预期基本一致。流动资产比率（LIAR值）对被解释变量的拟合系数为-0.701092，LIAR的拟合系数为负，负相关，并在1%的置信水平上显著，说明证券化造成了经营资产流动性增强，在拟合模型中LIAR值降低。在本文的拟合模型中，LIAR代表的是流动资产比率，是用来测度开展资产证券化业务后，商业银行资产流动性的变化情况，SLR代表的是证券化贷款比率，是用来测度商业银行开展证券化业务后，银行的各类风险（主要是信用风险）转移出去的程度，转移成本是否下降。

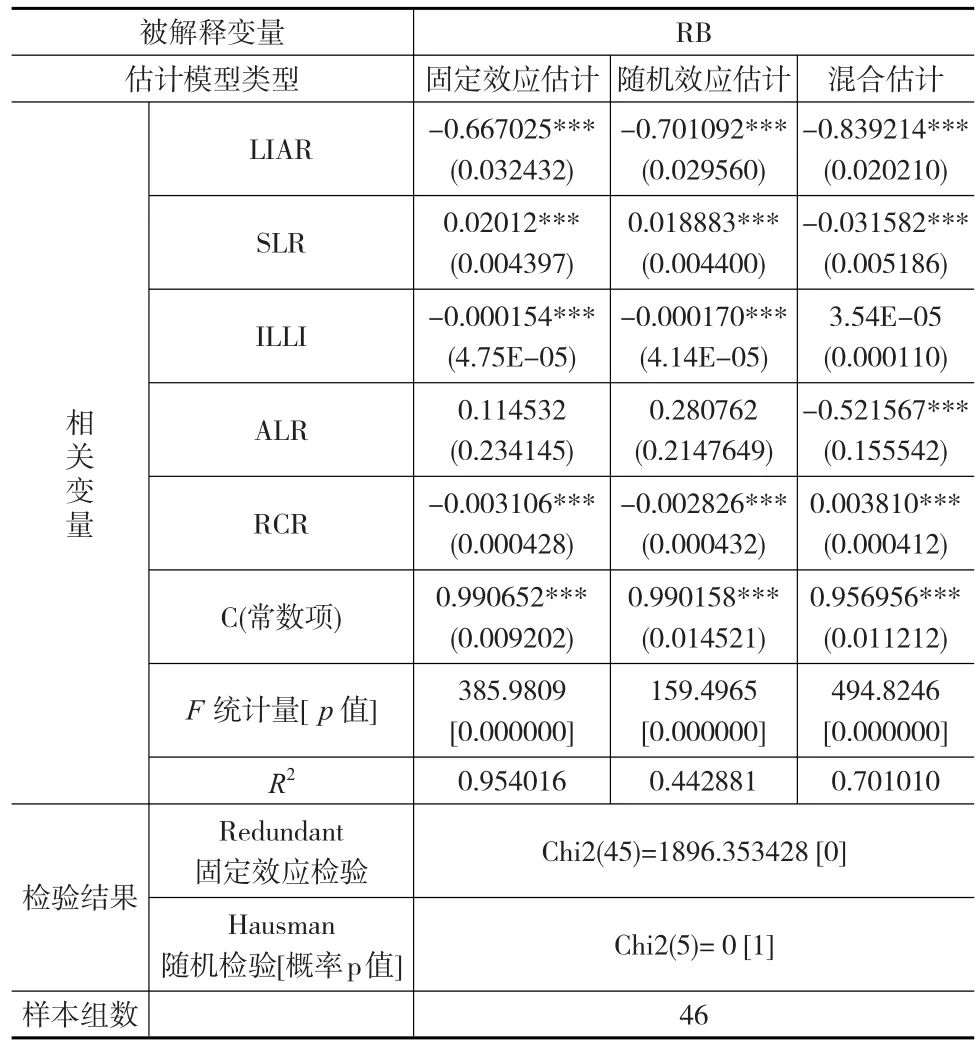
表2 总样本数据的拟合统计

2.2 子样本的实证结果

将46家银行控股公司的总体样本按照其资产规模，分为资产规模较大的23家银行控股公司和资产规模较小的23家银行控股公司两个子样本。本文在下页表3中列出了资产规模较大的公司相关分析变量的描述性统计。下页表4中列出了资产规模靠后的银行控股公司相关分析变量的描述性统计。下页表5和表6分别是采用资产规模较大的银行控股公司子样本数据，以及资产规模较小的银行控股公司子样本数据，采用三种面板数据模型拟合的结果。

表3 资产规模较大的银行相关变量的统计分析

表4 资产规模较小的银行相关变量的统计分析

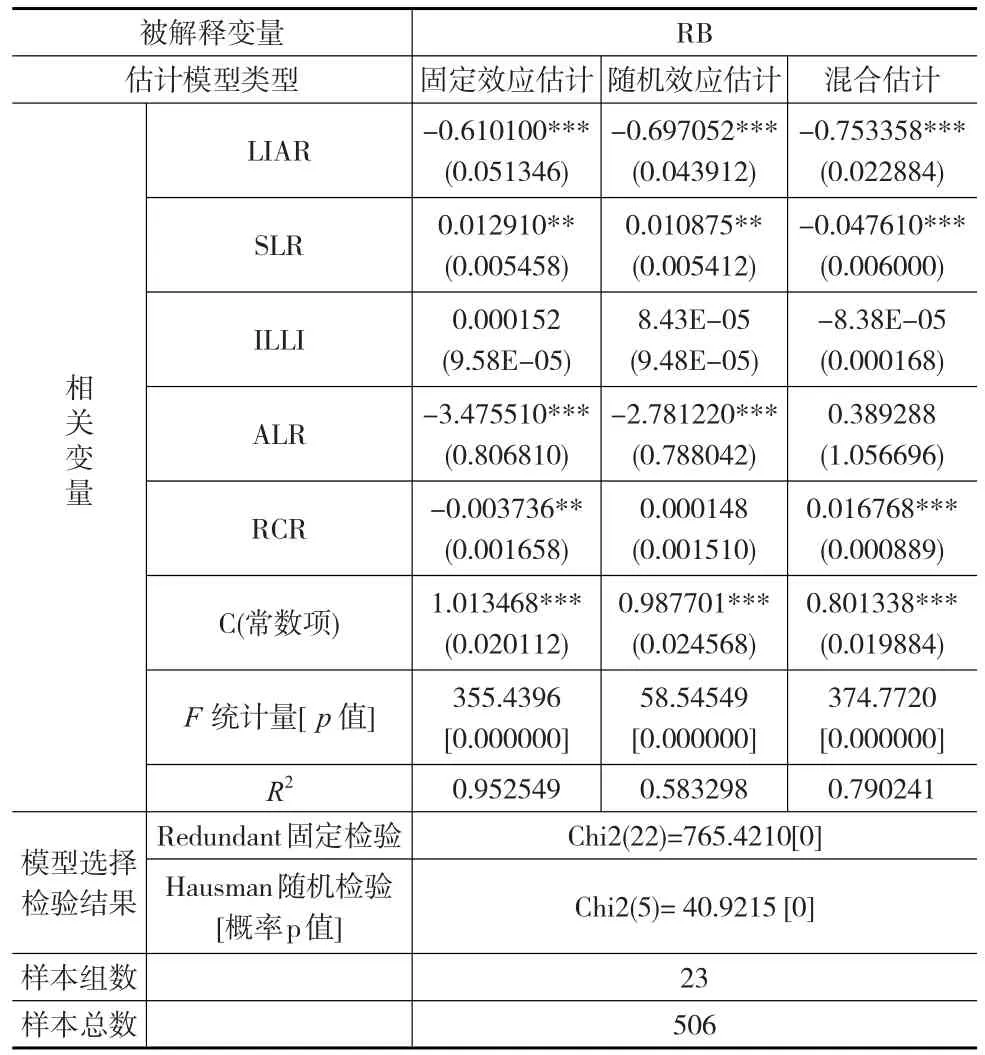
表5 资产规模较大的银行相关变量的拟合统计

从表5可以看出，Redundant固定效应检验的结果显著，概率值p取0，说明对样本数据来说，固定效应模型更适合。Hausman随机效应检验的结果也显著，概率值p取0，和Redundant固定效应检验的结果相同，即固定效应模型更适用，因此本文以固定效应模型分析为主。SLR的拟合系数为0.01291，并在5%的置信水平上显著，进一步发现其符号为正。LIAR的拟合系数为-0.6101，符号为负，并在1%的置信水平上显著，与预期基本吻合。另外也可以看出，代表市场流动性状况（ILLI）的回归系数为0.000152，结果并不显著，这说明对于资产规模较大的银行而言，银行行为动机受市场流动性的总体状况影响不大，主要还是根据银行自身的情况合理地调整风险承担水平。

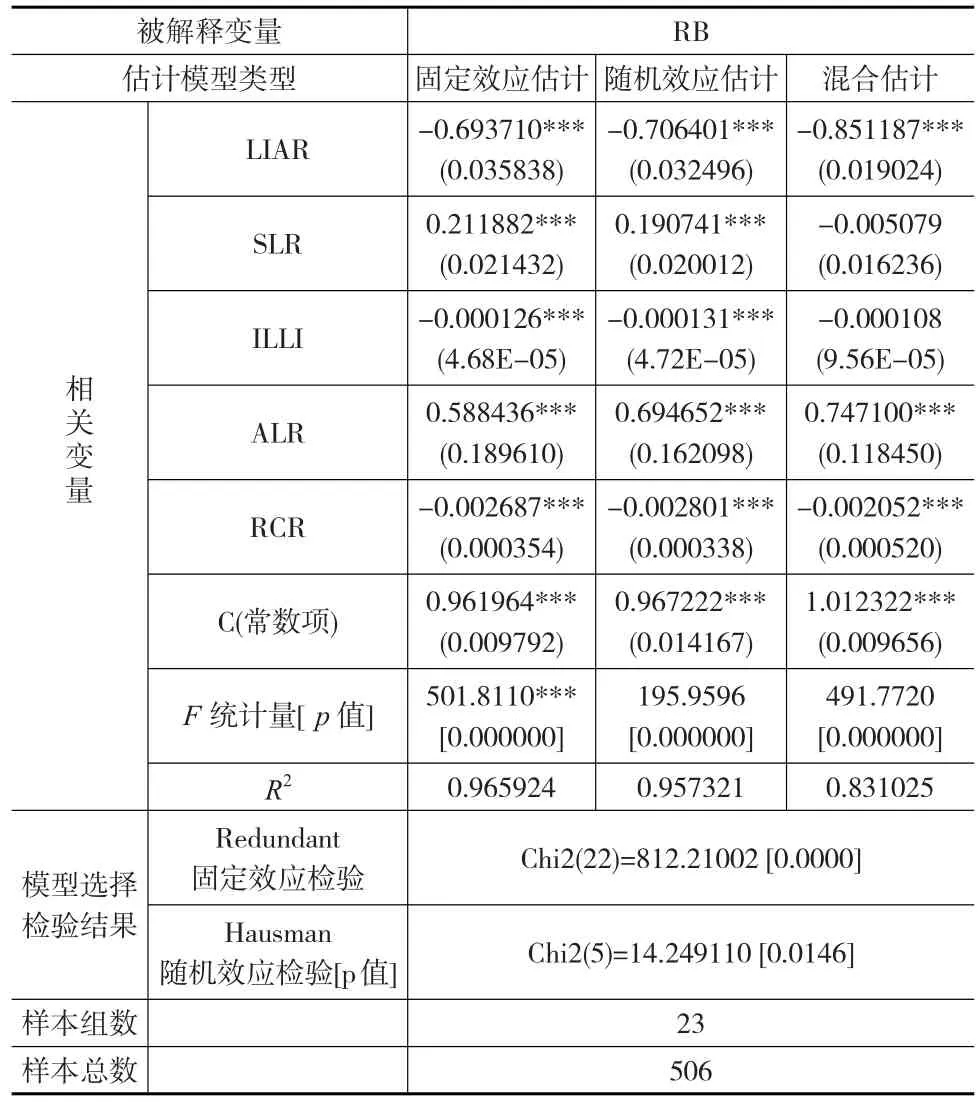
表6 资产规模较小的银行相关变量的拟合统计

从表6可以看出，Redundant固定效应检验的p值为0，Hausman随机效应检验的p值为0.0146，固定效应模型更适用。证券化贷款比率（SLR）的拟合结果在1%的置信水平显著，拟合系数为0.211882。LIAR的拟合结果在1%的置信水平上也显著，拟合系数为-0.69371，负相关。和资产规模较大的银行的回归结果相比，LIAR的回归系数绝对值较大，说明商业银行开展资产证券化业务后，资产流动性将会增强，这会导致规模较小的银行增加更大的风险承受水平。另外，ILLI的拟合系数为负，并在1%置信水平上显著，这和预期也基本吻合。说明对于对资产规模较小的银行来说，证券化市场的总体状况较为显著的影响对其行为动机，证券化资产在市场上越容易出售，资产规模较小的银行的风险承担水平会越高。

综合分析发现，不管商业银行资产规模是大是小，银行从事证券化后，其风险承担水平都会受到影响，影响路径通常有两种：一是资产证券化提高经营资产的流动性，降低转移成本，进而对银行风险承受水平产生影响；二是商业银行信用风险转移可以通过资产证券化业务来实现，进而会影响银行风险承受水平。表6的分析结果表明，SLR对被解释变量的回归系数的绝对值较小，LIAR对被解释变量的回归系数的绝对值最大，ILLI对被解释变量的回归系数的绝对值最小。这表明银行的资产证券化主要是通过改变银行资产流动性来影响银行风险承受水平。

3 结论

本文从商业银行风险承受水平的视角，探讨资产证券化业务对银行动机扭曲的影响，结果表明：

（1）商业银行开展资产证券化业务会扭曲银行的行为动机，进而给银行个体经营造成负面影响。理论研究认为有两条路径造成银行行为的动机扭曲：一是证券化转移了银行风险；二是证券化提高了资产的流动性。实证结果表明，资产证券化是通过提高资产的流动性，造成了银行行为的动机扭曲。尽管通过第一条途径也对银行的行为动机造成影响，但是影响甚微。

（2）商业银行开展资产证券化业务，增强了银行资产的流动性，造成了银行的动机扭曲。通过限制风险转移，增加风险敞口，来解决银行的动机扭曲问题是困难的。