隐状态个数未知的隐马尔可夫0-1分布的贝叶斯推断
2018-11-22刘鹤飞
李 勇,刘鹤飞
(曲靖师范学院a.信息工程学院;b.数学与统计学院,云南曲靖 655011)
0 引言
隐马尔可夫模型是一种基于随机过程的统计学模型。隐马尔可夫模型由两个随机过程构成,一个是状态转移序列、一条单纯的马尔可夫链;另一个是与状态对应的观测序列。在实际问题的研究中,只能看到观测序列的集合,而不能看到状态序列集合。也就是说,模型的状态隐藏在观测序列中,因此称之为“隐”马尔可夫模型[1]。隐马尔可夫模型的研究内容就是通过可观测的变量序列集合去推断不可观测的状态序列转移特征及每个状态下的分布信息。
近年来,马尔可夫模型在许多领域都有了极大的发展和广泛的应用。例如,在图像处理领域,沈杰等[2]利用隐马尔可夫模型改进了人脸识别技术;在语音识别领域,魏明哲[3]通过隐马尔可夫模型的分类识别提高了语音识别的效果;在生物医学领域,刘青等[4]通过隐马尔可夫模型实现基因识别系统的设计。在经济金融领域,孙鹏飞等[5]利用隐马尔可夫模型来拟合美元LIBOR相对美联储基准利率的变动情况。
虽然近年来关于隐马尔科夫模型的研究成果比较丰富,但是由于隐马尔可夫模型的复杂性,大多数研究都是关于隐马尔科夫模型的应用性研究,对于隐马尔科夫模型的纯理论性研究非常少。本文在已有的关于隐马尔科夫模型理论研究成果的基础上,研究隐状态个数未知条件下的隐马尔可夫0-1分布模型。首先利用可逆跳跃MCMC[6]方法对未知的隐状态个数进行贝叶斯模型选择;确定隐状态个数之后再用MCMC算法估计隐马尔可夫0-1分布的参数;最后生成观测数据集,实证模拟检验该方法的推断效果。
1 模型描述
观测变量yit来自0-1分布,其中i=1,2,...,N是观测对象,t=1,2,...,T是观测时点。Zit是系统观测对象在第t个观测时点的隐状态,其取值范围为{1,2,...,K},称为K个隐状态的隐马尔可夫模型。
假设模型不可观测的隐式链满足以下马尔可夫链条件:P(Zit=s│Zi1,Zi2,...,Zi(t-1)=u)=P(Zit=s│Zi(t-1)=u)=aus
其中:
u=1,2,...,K;s=1,2,...,K;i=1,2,...,N;t=2,3,...,T。
则aus是从前一个时点的隐状态u向后一个时点的隐状态s的转移概率。全部可能的隐状态转移概率构成一个矩阵,称为隐状态转移概率矩阵,记为:

隐状态转移概率矩阵的每一行之和为1。
在给定隐状态的条件下,隐马尔可夫0-1分布的观测变量定义为:

其中θj是第j个隐状态下0-1分布的参数,yit是0-1分布的观测度量,其取值仅为0或1。
2 贝叶斯推断
2.1 推断原理
记θ为不同隐状态下0-1分布的参数集合,即θ=(θ1,θ1,...,θk)。 则 该 模 型 的 贝 叶 斯 推 断 问 题 为P(K,Z,A,θ|Y),就是要根据观测度量的信息推断出模型的因状态个数K,隐状态集合信息Z,转移概率矩阵A,以及不同隐状态下0-1分布的参数θ。利用可逆跳跃马尔可夫链蒙特卡罗算法推断的具体执行步骤为:
(1)更新隐状态Z;
(2)更新隐状态转移概率矩阵A;
(3)更新0-1分布的参数θ;
(4)将一个隐状态分裂为两个,或者将两个隐状态合并成一个。
步骤(1)至步骤(3)中每一步更新参数都是普通的马尔可夫链蒙特卡罗算法,主要利用Gibbs抽样[7]和MH算法[8]从相关参数的全条件后分布抽样即可。步骤(4)是可逆跳跃步,在这一步中,允许以pk和qk=1-pk的概率增加或者减少一个隐状态。一般情况下,使增加一个隐状态和减少一个隐状态的概率相等,即pk=qk=0.5,但是q2=pmax=0除外。其中,q2=0表示隐状态个数为2时,再减少隐状态的概率为0;pmax=0表示隐状态达到设定的最大值时,再增加隐状态的概率为0;当隐状态为其他值时,增加一个隐状态和减少一个隐状态的概率是相等的,都是0.5。
2.2 先验分布
贝叶斯推断中,所有参数都看成是随机变量,所以,在进行贝叶斯推断时,要先为每一个参数选择一个合适的先验分布。本文借鉴已有的研究经验[9],为各个参数选取的先验分布如下:
Ak~D(α,α,...,α)
θj~U(0,1)
其中,Ak表示隐状态转移概率矩阵的第k行,D表示狄尼克莱分布,α是狄尼克莱分布的超参数。θj表示第j个隐状态下0-1分布的参数,为其选择的先验分布是(0,1)上的均匀分布。
2.3 全条件后验分布
贝叶斯后验推断主要是利用样本信息和参数的先验信息对模型进行推断。对于本文来说,即P(K,Z,A,θ|Y)。由于这个后验分布的复杂性,本文利用马尔可夫链蒙特卡罗方法来对后验分布进行模拟,这就需要推导相关参数的全条件后验分布。
隐状态Z的全条件后验分布P(Z|A,θ,Y)为:

也即:

其中,fk(Yt|θk)是观测变量在隐状态k下的似然函数。
由于隐状态转移概率只与隐状态的取值情况有关,所以P(A|Y,Z,θ)=P(A|Z),又因为A的每一行元素的先验分布都是对称的狄尼克莱分布D(α,α,...,α),所以每一行的全条件后验分布为:
P(Ak|Z)~D(α+nk1,...,α+nkK)
其中nki是前一个隐状态为k,后一个隐状态为i的样本总个数。
接下来推导0-1分布参数θ的全条件后验分布。当隐状态Z确定时,隐状态转移概率矩阵A也随之确定,此时第j个0-1分布的参数θj只与观测变量Yj有关,即P(θj|Y,A,Z)=P(θj|Yj),其中,Yj是隐状态为j的观测变量集合。
由于Yj1,Yj2,...,Yjn~b(1,θj),则Yj~b(nj,θj),也即:

由于θj的先验分布是U(0,1),则其概率密度函数为:

则样本Yj与参数θj的联合概率密度函数为:。

Yj的边际密度为:

利用贝叶斯公式可得θj的后验分布:

此式是参数为χ+1,nj-χ+1的贝塔分布,即θj的全条件后验分布为:
θj~Beta(χ+1,nj-χ+1)
2.4 可逆跳跃过程
1995年,Green[7]提出了可逆跳跃马尔可夫链蒙特卡罗算法,该方法通过在可变维参数空间中跳跃式抽样,实现贝叶斯模型选择的目的。1997年,Richardson[10]和Green利用可逆跳跃MCMC算法对正态混合模型中未知的混合个数进行选择。2000年,Robert[11]利用可逆跳跃MCMC算法对隐马尔可夫正态分布中未知的隐状态个数进行选择。本文借鉴以上研究方法,利用可逆跳跃MCMC算法对隐马尔可夫0-1分布中未知的隐状态个数进行模型选择。
可逆跳跃MCMC算法与普通的MCMC算法的主要区别是,在可逆跳跃步,允许未知的隐状态个数随机地增加或者减少一个,模型的参数发生相应的变化,最后以一定的概率接受或者拒接这种跳跃。以增加一个隐状态为例,可逆跳跃步的具体执行方法为:(1)从当前的k个隐状态中等概率随机的选择一个;(2)从预先给定的分布中生成一定数量的随机数;(3)利用生成的随机数,根据相应的分解方式,将选中的隐状态分解成两个;(4)以概率min(1,M)接受这种跳跃,其中:
M=似然比×先验比×跳跃比×建议比×雅克比
对于隐马尔可夫0-1分布来说,假设当前的隐状态个数为k,则有一个k阶的隐状态转移概率矩阵,有k个在0~1之间的参数θj。根据可逆跳跃MCMC算法的要求,增加一个隐状态,需要将k阶的隐状态转移概率矩阵增加到k+1阶,并且增加一个0~1之间的参数θ。将选中的待分解的隐状态记为j*,将j*分解之后的两个隐状态分别记为j1和j2。下面分别介绍生成随机书分解A和θ的具体方法。
Robert[12]根据矩阵的特征值,提出了一种能保留转移状态特征的转移概率矩阵的分解方法。以k阶隐状态转移概率矩阵分解为k+1阶为例,由于转移概率矩阵的每一行元素之和为1,因此k阶转移概率矩阵有k(k-1)个自由元素,k+1阶转移概率矩阵有(k+1)k个自由元素。下面介绍如何生成k(k+1)-k(k-1)=2 个随机数,对k阶转移概率矩阵进行分解。
首先生成t0~Beta(2,2),然后根据以下公式计算r和s:

其中,c2是Beta(r,s)的方差,根据经验,选择c2=0.3。
再从Beta(r,s)中生成随机数,使得:
uj~Beta(r,s),j=1,2,...,k且j≠j1,j2
vj~Beta(r,s),j=1,2,...,k且j≠j1,j2
记分裂前的转移概率矩阵A=aij,i,j=1,2,...,k;分裂后的转移概率矩阵为B=bij,i,j=1,2,...,k+1,则有:
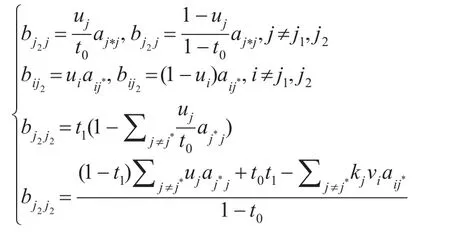
上式中,t0、uj、vj的生成方法已经介绍过了,最后来介绍随机数t1的生成方法。
令:

如果<,则没有符合条件的t1,隐状态转移概率矩阵分解不成功,分解跳跃过程立即停止。如果<,则在区间[,]上,随机地选择一个值作为t1。
以上就是通过生成随机数,将k阶隐状态转移概率矩阵分解成k+1阶的详细过程,这种分解方式不仅能保证每行元素之和为1,而且是可逆的,更重要的是能最大限度保留原来的转移状态特征。生成随机数,将0-1分布的参数θj*分解成θj1和θj2的方法比较简单,只需令ε~U(0,1),θj2=ε*θj*,θj2=(1-ε)*θj*即可。
最后来计算这种分解跳跃的接受概率。因为接受概率为min(1,M),且M=似然比×先验比×跳跃比×建议比×雅克比。每部分的表达式分别为:

其中,z1t是分解之前第i个观测对象在第t个观测点的隐状态,是分解之后第i个观测对象在第t个观测点的隐状态。

建议比 =[B1,2(t0)ΠjBr,s(uj)ΠjBr,s(vj)]-1
其中,B2,2表示Beta(2,2)分布的密度函数;Br,s表示Beta(r,s)分布的密度函数。

3 实证模拟
根据隐马尔可夫0-1分布的数学定义,生成一个观测变量数据集。首先利用可逆跳跃MCMC算法对未知的隐状态个数进行模型选择;然后在隐状态个数已知的情况下利用MCMC算法对模型的参数进行贝叶斯估计;最后将估计结果与模型参数的真实值进行比较,观察所给方法的推断效果。
取真实的隐状态个数k=2,观测对象个数N=500,观测时间T=10,转移概率矩阵两个0-1分布的参数分别为θ1=0.4,θ2=0.7。
取狄尼克莱分布中的超参数α=1,在使用可逆跳跃MCMC算法时,取迭代总次数为5万次,去掉前面的3万次,用后面2万次的结果来计算未知隐状态个数的后验概率。图1是5万次迭代过程隐状态个数的迭代路径图,表1(见下页)是隐状态个数的后验概率。

图1 隐状态个数迭代路径图

表1 隐状态后验概率
根据隐状态个数的后验概率结果,本文选择K=2作为未知的隐状态个数。然后再用MCMC算法取估计隐状态的转移概率和每个隐状态下的0-1分布参数值。超参数取值不变,MCMC算法的迭代总次数为8千次,去掉前面4千次,用后面4千次的后验均值作为未知参数的估计值,估计结果见表2。

表2 参数估计结果
4 结束语
本文研究了隐状态个数未知情况下的隐马尔可夫0-1分布的贝叶斯推断。首先为模型中的所有参数选择了合适的先验分布,并推导出了各参数的全条件后验分布,然后详细介绍了利用可逆跳跃MCMC进行模型选择时,可逆跳跃步的具体执行过程,包括随机数的生成方式、参数的分解方式、跳跃的接受概率计算公式等。隐状态个数确定之后,再用普通的MCMC算法估计模型中未知参数的值。最后,将模型的贝叶斯推断结果与设定的真实模型进行比较,发现利用可逆跳跃MCMC算法选出的隐状态个数与设定的真实隐状态个数一致,并且利用MCMC算法计算出的参数的后验均值也与模型设定的参数的真实值非常接近,这说明,该模型的贝叶斯推断效果良好。
本文的模型中考虑的是最简单最常用的0-1分布,0-1分布比较简单,分布中只含有一个未知参数,但其观测变量的取值只有0和1两个值,也导致观测变量的信息比较单调,所以该模型的推断也有一定的困难。今后的研究,可以在此基础上考虑更复杂的分布。
