人力资本统计核算方法研究述评

孟望生，张 扬

（甘肃政法学院 经济管理学院，兰州730070）

0 引言

1 成本法

自Schultz（1961）以后，人力资本的研究得到快速发展，形成了独立、统一的理论体系；该体系包括人力资本理论的基本原理、不同经济主体（家庭、学校、医疗机构以及企业等）的人力资本投资规律等众多理论和应用分支。Lucus（1988）提出“内生增长”理论后，人力资本的主要研究方向由原来的投资决定问题（人力资本为被解释变量）转向对经济增长等问题的解释（人力资本更多的变为解释变量）。与此对应，人力资本的应用领域也推广到经济增长、地区差异等众多方面。随着研究方向和应用领域的变化，人力资本核算方法的遴选变得至关重要。因为不同的核算方法直接左右了解释变量——人力资本指标的准确性，进而决定着其解释相关问题（经济增长、地区差异等）的合理与可靠性。当前，主要存在四类人力资本核算方法，具体为成本法、收入法、教育法、综合法。它们的核算角度、衡量体系和核算指标均不尽相同，从而具有不同的研究实用性和优缺点。本文对这四类方法进行梳理和评

成本法由Enge（l1883）[1]提出，主要是从投入回顾的角度核算人力资本，是早期人力资本核算的常用方法之一。基本假定为：第一，个人的人力资本等于其出生到成年的抚养成本；第二，随着年龄的增长，抚养成本呈线性增加；第三，一个人完全成年的年龄为男性26岁，女性20岁。同时，恩格尔还将人按收入分为三个阶层i=1，2，3（1、2、3分别代表低、中、高三个收入阶层），各阶层的子女抚养成本不同，分为生育成本c0i和年抚养成本c0i+kic0i两部分。一个成年人的人力资本为：

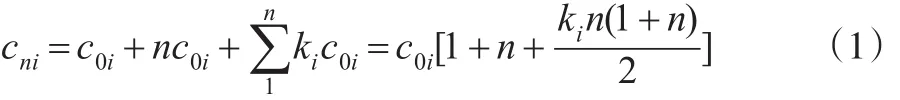
其中，n表示年龄；男性：n≤26；女性：n≤20；观察不同收入阶层人群的生育和抚养情况可以得出对应数据c0i和ki，然后代入式（1），得到对应阶层成年人的人力资本存量。

基本假定下，（1）式对人力资本的核算基本合理。但其计算过程中存在一些问题：未考虑货币的时间价值和机会成本（Dagum and Slottje,2000）[2]，即加总一个人的历年抚养费用时未进行贴现处理；同时个人成年前可能参与工作并获得收入进行自我抚养，这样可以减少其抚养成本。针对这些问题，Dublin and Lotka （1930）[3]对（1）式改进，得：

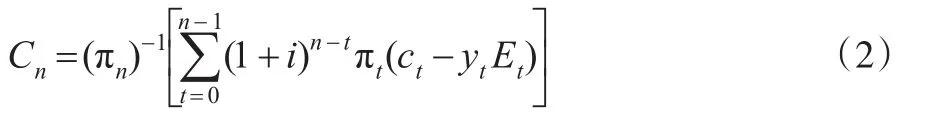
其中，Cn表示一个n岁的人所花费的抚养成本；πt表示个人活到t岁的概率；i为利率；ct和yt分别表示是个人从t岁到t+1岁的人均生活费和赚取的收入；Et则表示个人从t到t+1岁参加工作的概率。Dublin和Lotka（1930）[3]通过引入利率i和个人收入yt基本上解决了Engel（1883）[1]关于货币时间价值和机会成本的问题，使成本法的计算过程更趋合理。

该法创立于19世纪80年代，当时学者们研究人力资本的动机主要集中于考察一国国力强弱，或者核算战争、瘟疫等引起人口大量非正常减损的事件对一国国力的影响。在这一背景下，Engel（1883）[1]及其追随者Dublin 和Lotka（1930）[3]等的成本法具有一定的合理之处。然而，随着人力资本核算动机从国力衡量向经济增长贡献衡量的转变，该法基本假设也出现了诸多缺陷：首先，人力资本与人力资本投资相同。人力资本作为蕴含在人身上的相应能力是存量，而抚养成本是流量，充其量算作人力资本投资，这一投资不可能完全形成人力资本；其次，人力资本与消费相同。抚养成本中包括无法形成人力资本的消费，应将消费和人力资本投资进行区分。基于这些缺陷，Kendrick （1976）[4]和Eisner（1989）[5]有所改进，认为抚养成本是人力资本投资而非人力资本，且人力资本投资还存在有形和无形之分。具体为：促进个人体质成长方面的成本为有形的人力资本投资（主要发生在14周岁之前），旨在提高个人素质和劳动生产力方面的支出为无形的人力资本投资，主要包括：健康、安全、迁移、教育和培训、以及教育的机会成本。

诚然，Kendrick（1976）[4]和 Eisner（1989）[5]在早期成本法基础上有所完善。但其仍面临诸多理论和操作上的局限：首先，人力资本投资和产出之间的关系界定问题。Kendrick（1976）[4]关于人力资本投资和产出之间存在强正相关关系（1比1转换）的假定与现实不尽相符。因为其既没有考虑个人禀赋（如先天健康条件等）在人力资本形成中的作用，也未考虑人力资本投资和形成之间的时滞问题。其次，消费和人力资本投资无法完全区分。有些消费本身具有人力资本投资的功能。如青少年食物消费和营养投资之间，娱乐消费和智力开发之间等。Kendrick（1976）[4]将个人14周岁之前的消费视为人力资本投资的处理，仅简化了人力资本投资的计算过程，并未实质上区分消费与投资。第三，人力资本存量的折旧问题。Kendrick（1976）[4]，Eisner（1989）[5]采用和物质资本一样的会计折旧法来计算人力资本存量的折旧显然过于简单。人力资本除了折旧之外还应考虑其增值[6]，同时，人力资本还可能在个人年轻时增值，年老时贬值等[7]。

随着人力资本研究的焦点转向其对经济增长的贡献问题，成本法所面临的理论和操作难题使其无法满足研究需要。于是，学界开始从收入展望的角度寻求核算人力资本的方法。

2 收入法

收入法，主要从产出展望的角度核算人力资本，其基本思想是用个人未来的预期收入，或者“挣得能力”来核算人力资本。Petty等（1899）[8]最早用此法来核算一国的人力资本存量。后经Farr（1853）[9]，Dublin和Lotka（1930）[3]等逐步完善，形成了早期的人力资本收入法核算体系。与成本法相比，收入法用个人未来预期收入（生产能力）衡量人力资本，用于研究人力资本对经济增长贡献问题更贴切。所以，自卢卡斯将人力资本纳入索洛模型研究经济增长问题以来，收入法便伴随着增长问题的热捧而深受学者们青睐。为此，涌现出了众多从收入角度测算人力资本存量的方法。在此，对两种最具代表性的方法做评述。

2.1 J-F统计法

J-F 法是 Jorgenson 和 Fraumeni（1989）[10]核算当时美国人力资本总量时采用的方法。基本假定为：第一，个人的人力资本等于其终生收入，从而一国的人力资本就是该国所有公民终身收入的加总；第二，个人从事市场活动和非市场活动，因此其终生收入是市场活动和非市场活动收入（机会成本）之和；第三，其他条件相同的情况下，当前年龄为a的个人n年后的年收入与当前年龄为a+n个人的现期收入相同。通过这些假定，Jorgenson和Fraumeni（1989）[10]将美国人按性别、年龄和教育层次进行分组（共分为2196组），建立了计算代表性行为人终生收入的模型：

其中，下标s，a，e，y分别代表性别、年龄、受教育层次、年份；参数g，r分别表示经济增长率和利率；Y代表年收入，Sa+1表示a岁的人存活至下一年的概率；V代表对应个人的终生收入。该式表达的基本思想是：在性别和受教育层次一定的前提下，在y年份，a岁的个人，未来终生收入等于其当期（年份为y）收入与下一期未来终生收入加权的现值之和。通过递归运算可以计算出既定性别和受教育层次下任一年龄上代表性行为人的终生收入。也就是说，可以计算出任何年份各个组内，代表性行为人的终生收入。最后通过加总便可获得一国人力资本存量。

随后，Jorgenson 和Fraumeni（1992）[11]又在Jorgenson 和Fraumeni（1989）[10]基础上进行改进：将人的一生划分为三个阶段（具体为：个人在第一阶段只上学，在第二阶段既上学也参加工作并获得收入，在第三阶段只工作），建立了处于两种状态（工作和边学习边工作）人群的收入计算模型：

其中，E表示入学率。

与早期收入法相比，J-F法的主要贡献是简化了未来收入的贴现过程。早期收入法计算过程较麻烦，需要将个人终生收入逐年贴现到生命的第一期后再加总。而J-F法可以将处于任何年龄个人的收入直接加总。同时，该法还将在校生的潜在价值纳入人力资本核算当中，使人力资本的核算更加全面。然而，J-F法也存在一些问题：第一，非市场活动纳入分析的合理性问题。J-F法将个人非工作时间（非市场活动）进行全面核算的做法忽略了失业对个人收入和一国人力资本的影响[12]。同时还忽视了非市场活动时间对工作的影响，因为工作时需要一些闲暇时间做准备[13]；第二，对年教育回报的估计存在偏差，Jorgenson和Fraumeni（1989）[10]用多接受一年教育个人终身收入增加的现值估计年教育回报，缺乏对教育机会成本，尤其教育时间价值的考量；第三，个人能力的估计偏差问题。该法假定相同条件（即相同教育水平，性别特征和年龄）个人的未来收入均相同，同时，还将所有类型的教育回报进行均等化处理。这一假定忽略了个人禀赋的差异和教育回报的差别[2]。另外，Jorgenson 和 Fraumeni（1989）[10]中对个人退休年龄的设置过高（75岁）会导致个人终生收入的高估，最终引起人力资本的过高估计。基于J-F法的这些缺陷，学者们进行了新一轮的探索，建立了收入指数法，其中LIHK法最具代表性。

2.2 LIHK统计法

LIHK 法由 Mulligan 和 Sala-i-Martin（1997）[14]提出，将劳动力与教育相结合来核算力资本。基本步骤为：首先从总体劳动者中剥离出未受过正规教育这一类型的劳动者，观测并求其平均工资；然后以这一平均工资为基准（或称作单位人力资本，下同）去除任一劳动者的工资，相除结果即为该劳动者的人力资本。计算公式为：

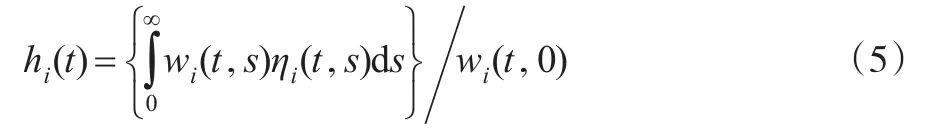
其中，下标i表示待核算的国家或者样本点；t，s分别代表时间和受教育年限；hi（t）表示相应时期和国家的人力资本存量；wi（t，s），ηi（t，s）分别表示对应劳动者的工资率和这一劳动者占劳动者总数的比例；wi（t，0）为未受过教育劳动者的平均工资。

经济环境以及与之相匹配的物质资本水平等个人能力之外的因素会影响个人收入，从而使收入法核算的人力资本水平产生偏差。例如，同等技能水平的工人在经济发达的地区收入较高；地区间（同一地区不同时期间）物质资本水平的差异会使得具有相同教育水平的劳动者间存在工资差异等。而LIHK法则通过个人收入与基准工资相除的办法在一定程度上消除了这一偏差，因为基准工资有效的包含了经济环境和物质资本水平的差异。另外，LIHK法还具有以下优点：第一，放松了受教育水平相同的劳动者具有同等能力水平（人力资本）的假定；第二，允许不同劳动者之间的替代弹性存在差异；第三，这一方法在估计人力资本时不需要大样本数据，估计较为方便可行。

然而，基准工资的选择会使该法产生新的问题：Mulligan和 Sala-i-Martin（1997）[14]选择未受正规教育劳动者的工资作为基准工资意味着不同国家（或同一国家不同时期）的未受过正规教育的劳动者具有相同的人力资本水平。这忽略了非正规教育、工作训练、健康水平以及能力等因素对个人收入的影响。为有效控制这一问题的影响，Tao和 Stinson（1997）[15]、Jeong（2002）[16]以及朱平芳等（2007）[17]都在基准工资选择上作了不同尝试。Tao和Stinson（1997）[15]选择新就业者（大学毕业后直接进入劳动力市场的人）工资为基准。由于新就业者未接受任何形式的在职培训和非正规教育，从而可以减小由非正规教育和在职培训产生的估测误差。另外，Tao和 Stinson（1997）[15]还采用 Scholastic Aptitude Test得分来衡量新就业者能力，以期消除个人能力对收入的影响。Jeong（2002）[16]选用工业工人的平均工资为基准。他认为测度和比较不同国家人力资本存量时，选择工业工人的平均工资为基准更合理。因为工业工人主要从事体力劳动，技术含量都较低。同时，他们体力相近，健康程度相当。这些特点使得不同国家的工人人力资本更接近。如果说 Tao和 Stinson（1997）[15]以及 Jeong（2002）[16]在试图选择一个更为合理的基准工资的话，朱平芳等（2007）[17]则试图构造一个基准工资，其假定经济中的单位人力资本不仅没有受过正规教育，而且没有任何教育、工作经历；单位人力资本只具备一些基本的能力：健康的身体以及一些最为基本的能力（如语言等）；单位人力资本只能从事一些最简单的生产活动；除此之外，没有任何生产技能。

LIHK法减小了地域因素和经济发展水平对人力资本的影响，是收入法核算人力资本的一大进步。但不论是未受过正规教育的劳动者工资，还是工业工人的工资，再或是朱平芳等（2007）[17]构造的单位人力资本，都会引入一些新问题。如未受过正规教育劳动者的工资在不同地区间存在差异；不同地区工业工人的工资同样存在差异；朱平芳等（2007）[17]中具有单位人力资本的劳动者在现实中并不存在。人们无法观测到单位人力资本，进而需要通过物质资本和产出数据换算。人力资本的核算受到换算误差和数据可得性的影响。与此同时，朱平芳等（2007）[17]对产出函数的假设（假设为C-D型函数）过于主观。

3 教育法

教育法指采用诸如成人识字率、入学率、人均受教育年限、教育质量（考试成绩等）等反映教育投资和产出的指标来代换人力资本水平，对这些指标进行核算的一种方法。基本原理为：教育是构成人力资本的关键要素，以上指标反映了教育投资和产出情况，从而能一定程度上反映一国人力资本水平。

3.1 成人识字率与入学率

成人识字率指15岁以上人口中，对简单日常用语具有读写能力的人口所占比重（UNESCO,1993）。入学率指各级教育（学校）的入学人口占适龄入学人口的比重，分为净入学率和总入学率；总入学率是用相应层级学校的总入学人口除以适龄人口，净入学率则是用相应层级学校的适龄入学人口除以适龄人口。这两类指标因其国际标准统一、数据易得等特点曾受学者青睐。如Romer（1989）[18]用成人识字率估计了人力资本和经济增长之间的关系；Barro（1991）[19],Mankiw 等 （1992）[20],Levine 和 Renelt （1992）[21]，Gemmell（1996）[22]都采用经过时滞调整的入学率核算人力资本。然而，这两类指标也缺点诸多。比如，成人识字率概念本身界定不清，主观性强，且忽略了更高水平教育和个人能力对人力资本的影响；作为流量指标的入学率对作为存量指标的人力资本的代替，无法反映当期人力资本水平。介于这些缺点，学者们在后来的研究当中，几乎很少采用这两类指标直接代替人力资本水平。而是当其他更好人力资本替代指标（如平均受教育年限等）存在数据缺失时，将其作为辅助工具用以换算其他教育指标。如Kyriakou（1991）[23]根据以往入学率和平均受教育年限的关系，对大多数国家缺失年份的平均受教育年限数据进行了估计；Barro和 Lee（1993,1996）[24，25]在核算 1960—1990 年世界上绝大多数国家教育分布情况时，也采用入学率估计相应国家的平均受教育年限。

3.2 平均受教育年限

与以上成人识字率和入学率相比，平均受教育年限作为人力资本的替代指标更为合理。因为平均受教育年限和人力资本同为存量指标，且正规教育的量（即教育年限）在一定条件下能准确地反映人力资本水平[26]。如此一来，如何准确核算一国的平均受教育年限便成为人力资本核算准确与否的关键，目前比较常见的核算方法有以下几类：

3.2.1 常规方法

常规方法由 Psacharopoulos和 Arriagada（1986）[27]提出，是核算一国平均受教育年限最常用的方法，计算公式为：

其中，ˉ表示一国国民的平均受教育年限；i表示不同的教育层次（包括文盲、小学、初中、高中、大学）；YRi表示完成i层次的教育所花费的总时间（以年计）；HSi表示一国具有i教育水平的人口所占比例。

常规法是估计平均受教育年限的最基本形式，操作简单。只要拥有一国人口的受教育结构和各个层次教育完成年限的数据便可用此法估算其平均受教育年限。常规法的缺点是没有考虑同一层次教育的人受教育年数不同的情况，如因为留级等原因，有些人可能需要花费更长时间来完成某一层次（小学、中学等）的教育。与此同时，当一国人口受教育结构数据存在较大缺失时（发展中国家较为普遍），该法将无法直接测度平均受教育年限，需要通过Kyriacou（1991）[23]和提出的投影法加以解决。

3.2.2 投影法

投影法的基本原理是用各层次教育的入学率来估计平均受教育年限。根据我国教育体制，将原公式具体化为：

其中，为t时期（年）劳动力的平均受教育年限；University，High，Sec，Prim分别代表大学、高中、初中、小学在相应年份（下标）的入学率。这一方法旨在通过已有数据的回归，得出入学率与平均受教育年限之间的关系，然后预测未来或者数据缺失年份的平均受教育年限。该法是在一国人口受教育结构数据缺失的情况下估算平均受教育年限的另一方法。

3.2.3 永续存盘法

Lau等（1993）[28]首次采用了永续存盘法建立了全球58个发展中国家1965—1985年的教育存量时间序列。基本操作原理为：首先将适龄工作（15岁以上）人口的总教育年数定义为教育存量并计算，然后用教育存量除以适龄工作人口数得出平均受教育年限。在此，教育存量成为计算平均受教育年限的关键，可用永续存盘法累加适龄人口在各个年级的入学人数计算得出：

其中，下标T，t，g分别代表考察年份，个人入学年份和入学年级；Eg，t表示第t年g年级的入学人数；θg，t表示在t年进入g年级的学生存活到考察年T的概率。αmin为工作年龄下限，αmax为工作年龄上限，可以根据不同国家的具体情况规定工作年龄的上下限。Lau等（1993）[28]中规定的个人工作年龄上下限分别为64岁和15岁，入学年龄为6岁，T-15+6和T-64+6便分别为最年轻和最年长劳动者的入学时间。

考虑到辍学和重复入学可能引起对教育存量的高估，Nehru等（1995）[29]引入辍学率d和重复入学率r对Lau等（1993）[28]加以修正，具体为：

与式（8）比，式（9）剔除了辍学率和重复入学率对教育存量的影响，在理论上更具合理性，但其又面临d和r的确定问题。Nehru等（1995）[29]中d和r恒定不变的假定过于主观，这一做法很可能在修正一个偏误的同时又给估计引入新的偏误；此外，孟望生和王询（2014）[30]还在借采用永续盘存法的基础上从成本角度对我国各省级地区的人力资本存量进行了测度。

相对于常规法和投影法，永续存盘法对教育存量，进而对平均受教育年限的估计更加准确。该法对每一年级入学适龄人口数量的累加，解决了同一层次教育人存在不同受教育年限的问题。同时，该法通过每年级适龄入学人口数量来估算平均受教育年限也要比常规法（只考察每一层次的教育年限，每一层次存在多个年级）和投影法（用入学率估算教育年限）更细致。然而这一方法对数据的要求很高，涉及数据序列的时段过长。如，倘若估计当前15～64岁人口的总教育年数，就必须掌握58年以前有关入学率和人口死亡率的数据。这就要求估测对象国相关数据长期保存完整，统计口径保持一致。即使这些条件完全满足，永续存盘法也会面临辍学、重复入学的两难境地①在估计教育存量时，辍学率和重复入学率的缺失会引起教育存量的高估，而伴随着这俩指标的引入又会产生对其本身估计的偏误。。

平均受教育年限的测度方法各具特点。在具体研究中，需根据具体情况加以甄选，以使测量数据尽可能准确。然而，用平均受教育年限替代人力资本存量却暗含着如下假设：教育质量在空间和时间上无差异，即接受相同年限的教育在不同国家（或地区）或不同层次（小学和大学）上所形成的人力资本水平是相同的。事实上，国家间（甚至同一国内不同地区间）的教育质量差异很大，且教育素质也随时间变化。如贫穷和富裕的国家，中国的东部地区和西部地区，其教育质量的差别是显而易见的。对教育质量差异性的忽略也可能是实证研究并未支持平均受教育年限和生活标准的提高之间存在稳定关系的原因[31]②St.Gallen,Switzerland（2010）发现全球各个国家人口的平均受教育年限均存在长期增加的趋势，但生活标准没有这种趋势。为此，还需要将教育质量纳入教育核算方法体系。

3.3 教育质量

长期以来人们很少关注教育质量，主要原因是人力资本数量变化比质量更重要，且数量指标（教育年限、入学率等）更容易衡量。随着研究的深入，教育质量的衡量变得愈发重要。Barro和Lee（1996）[25]首先作了这方面的尝试，他们用师生比、人均公共教育投入等指标衡量教育质量。接着，Lee和 Barro （2001）[32]用国际成人阅读能力考试（the International Adult Literacy Test，简称 IALS）成绩来衡量相关国家的教育质量。较 Barro和 Lee（1996）[25]，Lee和 Barro（2001）[32]教育质量的衡量指标更加合理，因为后者采用指标反映了教育产出，而前者反映教育投入。随后，Hanushek 和Kimko（2000）[33]结合更多指标建立了一个衡量教育质量的指数，使得教育质量的衡量趋于完善。

然而，将一国人力资本用教育质量代替存在诸多问题。因为教育质量本身包含了诸多不可观测的因素。如考试分数高低受个人能力的影响，当前在校生所体现出的教育质量和这些学生在未来成为劳动者后的质量之间可能存在较大差别等。鉴于这些问题，Wößmann（2003）[34]用教育质量和教育年限结合的方法测量人力资本。该法基本思路为：首先，以美国教育质量的数据为基准，去除其他国家教育质量的数据③数据来自Wanushek and Kimko（2000）测量的结果。得到各国的教育质量指数。其次，以这一指数为权数，结合教育数量指标（平均受教育年限）与教育回报率求得不同国家的人力资本存量。具体为：

式（10）也称作质量调整后的人力资本存量。其中，下标i和α表示相应的国家和教育层次（如小学、初中等）；Qi表示i国的教育质量指数；Sαi为一般情况下，完成i国α水平的教育需要的平均受教育年限；ra表示α层次教育的世界平均回报率。

和传统教育法相比，Wößmann（2003）[34]的方法具有两大进步：第一，用教育质量和数量相结合的办法测量人力资本，使测量方法更加科学。第二，打破传统上人力资本存在上限的思维定势，认为人力资本可以持续增长。但是，由于该法的实现需要用到教育质量和数量数据，所以教育质量和数量数据的测量误差，将形成人力资本核算的偏差。

教育作为人力资本的重要构成要素是基于教育方法核算人力资本的重要理论依据。然而不论对教育的衡量如何全面、准确，教育指标也不能完全反映人力资本水平。因为教育只是构成人力资本的一方面（或纬度）要素。根据人力资本的定义（OECD,2001）可知，人力资本是一国（或者一个人）多方面能力的体现，其构成要素来自多方面。因此，对其更准确核算需要综合考虑各个方面的因素。

4 多元综合法

多元综合法是指将“回顾”和“展望”视角相结合④“回顾”（retrospect）的视角指：估测人力资本时以其形成前的投入为主要考察对象的角度。考察对象包括成本法涉及的指标和教育法中部分反映教育投入的指标；“展望”（prospect）的视角指：以人力资本形成后的反映指标为主要考察对象的角度，考察对象包括收入法涉及指标和教育法中部分反映教育产出的指标。，综合考虑涉及人力资本多个方面反映指标，选择一个恰当的模型赋予这些指标（收入法、支出法、教育法指标）一定权重来计算人力资本综合得分的统计方法。其原理是：将人力资本（HC）定义为一个由其各形成要素组成的潜变量：z=l（f1，...，fj，...，fp）=l（F）；然后通过其与反映指标（主要指收入）之间的关系赋予各形成要素一定的权重来计算人力资本综合得分，这一得分便能衡量人力资本水平。Földvári和 van Leeuwen （2005）[35]、Le（2006）[36]以及 Dagum 等.（2007）[37]分别运用此法估计了东欧（1993年）、新西兰（1995年）以及美国（2004年）的人力资本水平。Klomp（2013）[38]、王询和孟望生（2014）[39]在这些方法的基础上建立了较为完善的综合法估计体系。该体系在人力资本是由多个形成指标构成的高阶潜变量的假定下，利用因子分析给各形成指标赋予相应权重的方法，进而计算人力资本的综合得分。计算出的综合得分可以反映不同国家（地区）和不同年份的人力资本水平及其变化情况。

多元综合法是对支出法、收入法以及教育法的综合。其对人力资本各形成要素的选择体现了支出法的基本思想，且将教育指标包含其中；同时，对各形成要素权重的选择考虑了这些要素与收入的关系。综合法的运用需要搜集大量涉及人力资本各指标的数据，并对其进行量化处理。

5 结论与展望

成本法和收入法分别从“回顾”和“展望”（未来赚钱能力）的角度核算人力资本；而教育法则直接将教育存量（如平均受教育年限、成人识字率等）视为人力资本，既包含了对教育投入的“回顾”又包含了对教育产出的“展望”，在人力资本考察角度上更具全面。然而，教育不是构成人力资本的唯一要素，即人力资本的形成和变化受到多重因素的影响。因此，一个更为合理的人力资本核算方法需要更加全面地考虑人力资本的多维性特点。综合法正是基于这一考虑的结果。

见图1：这些核算方法及对应指标之间相互联系，互为补充，共同构成了人力资本核算方法体系。人力资本作为与经济活动相关的个人知识、技能、能力等特性的综合，既可以通过投入获得，又能通过产出反映。如教育法中部分指标和成本法体现人力资本投入的同时，其另一些指标又和收入法反映人力资本产出；教育作为人力资本的代换指标一定程度上是人力资本投入和产出的桥梁，具有综合性的特点。而综合法则在教育法的基础上更进一步，综合考虑人力资本投入和产出的同时，将包括教育在内的尽可能多的人力资本相关指标纳入其中，实现人力资本核算的多维性，是对三类方法的糅合。

图1 人力资本核算方法和指标体系

在具体研究中，要根据研究目的和掌握数据情况选择恰当的方法进行人力资本核算。早期研究中，人力资本的核算动机是为了估测一国国力或者战争、瘟疫等灾难引起人口缩减所造成的国力（或经济）损失。在这一研究动机和背景下，选择成本法测度人力资本具有其合理性。20世纪70年代以来，人力资本核算主要服务于探究经济增长的源泉。于是核算方法也更多地选择收入法（主要为LIHK法）和教育法。然而，得到理论论证的观点——人力资本是经济增长的主要源泉之一，却并未得到实证的一致支持。究其原因，源自人力资本核算偏误。因为收入法和教育法（包括成本法）均存在两方面的误差：人力资本构成要素遗漏误差和数据测度误差。综合法的出现会使人力资本要素遗漏造成的误差大大降低，将是未来一段时期人力资本核算的主要方法。但这一方法还是无法穷尽所有人力资本构成要素，同时对指标数据测度误差无能为力。