Gompertz曲线参数估计的一种加权方法
2018-11-22王增辉赵彦军姜淑珍黄东岩
王增辉,赵彦军,姜淑珍,黄东岩
(1.东北师范大学 人文学院,长春 130117;2.吉林大学 工程仿生教育部重点实验室,长春 130025)
0 引言
Gompertz曲线是一种生长曲线,已广泛用于描述动物的生长规律和植物中某些物质(例如大豆中的蛋白质以及脂肪)的增长规律。在人口学和经济领域的研究中也有广泛的应用。Gompertz曲线是英国统计学家和数学家Gompertz通过大量观察和研究提出来的。它的一般表达式为:

其中a>0,b>0,k>0。
关于Gompertz曲线中的参数a,b,k的估计。目前的估计方法是先用三点法或四点法来估计参数a,而参数b与k的估计则是将式(1)取对数然后化为曲线模型。最后用普通最小二乘法来估计。本文给了一种估计Gompertz曲线参数估计的加权最小二乘法。通过实例分析可知,本方法相对于不加权的最小二乘法估计法得到的Gompertz曲线拟合效果有明显的提升。
1 Gompertz曲线参数估计的普通最小二乘法
1.1 Gompertz曲线参数a估计的三点法、四点法
将式(1)变形为:

设给定一组数据 (ti,yi)(i=1,2,…,n)。这里假设xi为等距。即设xi+1-xi=h(i=1,2,…,n-1),h为常数。若n为奇数,取三个点,并带入式(2)中可解出:
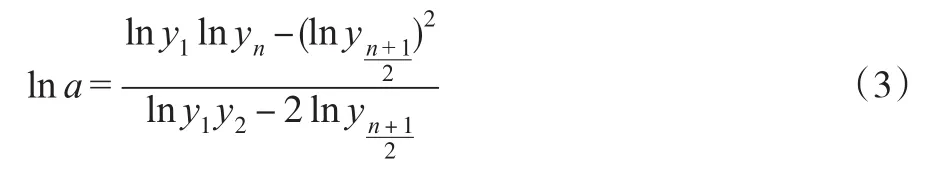

则由式(3)或式(4)可估计出Gompertz曲线中的参数a。
1.2 Gompertz曲线参数b与k的最小二乘估计
对式(2)两端取自然对数得:


式中的参数A与B可用最小二乘法来估计,其估计公式为:

其中:
t_=于是可估计出Gompertz曲线中的参数
2 Gompertz曲线参数估计的加权法
上面估计Gompertz曲线中参数b与k时,是将式(1)两端两次取对数化为线性模型(6)来估计的,由于做了变换,可能破坏等方差的假定,因此应用普通最小二乘法估计式(6)中的参数A与B(从而估计出非线性模型(1)中的参数b与k),可能不理想。对此本文给出了一种估计参数b与k的加权最小二乘法,下面介绍这种加权最小二乘法,这是式(1)中的参数用三点法或四点法来估计。
由多元函数极值原理有:

解此方程组可得A与B的加权最小二乘估计为:
显然若取wi相等,则式(8)就是式(7),因此式(7)是式(8)特例。
对于权wi的选取有多种方式,由于权wi与模型(1)化为线性模型时所做的变换Y=f(y)有关。即权wi与成正比。由于可以取权:

由此可取权:

在实际计算时,可将式(8)写成如下公式:

对给定一组数据 (ti,yi)(i=1,2,…,n),将数据代入式(9)中可估计出式(1)中的参数b=eA,k=-B。
3 Gompertz曲线拟合精度的度量
关于曲线拟合的精度的度量,通常选用相关指数R2和残差平方和Se来度量。
相关指数R2定义为:

残差平方和定义为:

显然残差平方和Se越小,说明曲线拟合越好,而相关指数R2越接近于1,说明曲线拟合的越好。
4 实例
下面通过实例介绍Gompertz曲线参数的加权方法,并给出用普通方法求出的Gompertz模型与本文方法给出的模型进行精度比较。
4.1 实例一
首先探讨大豆的叶面积随时间增长的规律问题。数据如表1所示、
由于共有10个数据,即n=10,因此可用四点法来估计Gompertz曲线中的参数a,选用四个数据,y1=0.4,y5=3.0,y6=3.6,y10=4.8,代入公式(4)中可估计出=4.8624,再将表1中的数据yi进行变换:
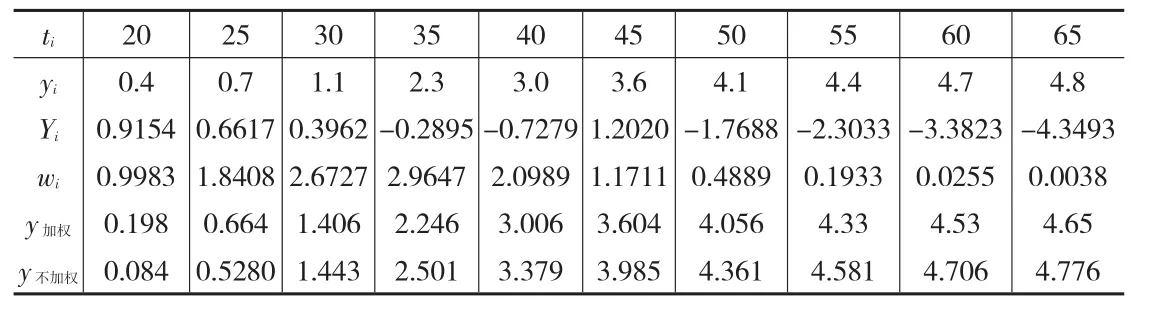
表1 大豆的叶面积指数y(t)与生长日数t之间的关系

并列入表1中,并求出权wi列入表1中,同时可计算出:

由公式(8)可估计出:

于是可估计出Gompertz曲线参数的加权估计为=eÂ=21.32003,k̂=-B̂=0.0948,因此得描述大豆面积的Gompertz曲线为:

为了比较加权参数估计方法与不加权参数估计方法所得的Gompertz曲线的拟合精度,本文求出不加权的Gompertz曲线模型:
由表1中的数据可求出:

由公式(7)可估计出:

于是求出b与k的估计值分别为:
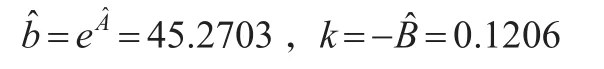
由此得到描述大豆面积生长规律的不加权Gompertz曲线模型为:

现在比较一下参数加权估计与不加权参数估计得到Gompertz模型(12)与(13)的拟合精度,用模型(12)与(13)分别计算出在各ti处的预测值分别列入表1中,再由公式(10)与(11)求出:

由此可看出加权参数估计方法的拟合精度比不加权参数估计方法的拟合精度有明显提高,若从残差平方和的角度看,加权方法的误差是不加权的误差的三分之一。
4.2 实例二
某地区1993—2010年某种家电销售量分析,数据来源于《中国统计年鉴》,具体数据如表2所示。

表2 家电销售量(千台)y(t)与年份t之间的关系
家电销售量随时间增长规律和趋势比较符合用Gompertz曲线模型来拟合。由于数据总数为18为偶数,首先用公式(4)来估计模型中的参数a,因此选用四个数据y1=1.2,y9=178,y10=246,y18=478代入公式(4)中可求a的估计值为a=500.6 ,然后将已知数据tilna=ln500.6,yi,代入公式(9)中可求出A加权=3.0137,B加权=-0.3332,于是可估计出b加权=eA加权=20.3629,k加权=-B加权=0.3332。从而得到描述家电销售规律的Gompertz曲线模型为:

下面再用普通最小二乘法求出描述家电销售规律的Gompertz曲线模型。
由于参数a已由前面估出。只需估计参数b与k,将数据代入式(7)中可估计出A不加权=3.0027,B不加权=-0.3002 ,得到不加权k不加权=-B不加权=0.3002。于是求出不加权情况下描述家电销售规律的Gompertz曲线模型为:

现在对两种不同方法得到的Gompertz曲线的拟合精度进行比较。由公式(10)与(11)可计算出两个模型的残差平方和与相关指数分别为:

由此可以看出加权参数估计方法的精度在显著提高,从残差平方和可知不加权的残差平方和是加权的残差平方和的15倍之多。
5 结论
(1)本文给出的Gompertz曲线参数估计的加权方法相比不加权方法,其参数估计的精度都有所提高,特别是当给出的测试数据波动比较大时,精度提高更为明显。
(2)若在公式中取权wi=w(常数)(i=1,2,…,n),则公式(8)就是公式(7),因此公式(7)是公式(8)的特例。
(3)关于权wi(i=1,2,…,n)的选择有多种方法,例如可以选择wi=,也可以选择wi=,k为常数,由权wi的选取不同,其参数估计的结果也不同。
