基于TF-IDF算法的P2P贷款违约预测模型
2018-11-22章宁,陈钦,2
章 宁,陈 钦,2
(1.中央财经大学 信息学院,北京 100081; 2.国银金融租赁股份有限公司 信息化管理部, 广东 深圳 518038)(*通信作者电子邮箱2013110160@CUFE.edu.cn)
0 引言
个人对个人P2P(Peer-to-Peer)借贷(或P2P贷款)即个人对个人的贷款行为,投资人依据借款人的个人信用,按照一定利率进行贷款投资,一旦出现违约,贷款本金将产生较大损失[1-2],具有收益固定、风险高的特点。
全球第一家在线P2P借贷平台是2005年成立于英国的Zopa。美国两家最知名的P2P借贷平台,分别是成立于2006年的Prosper,以及成立于2007年的Lending Club,后者于2014年12月在纽约股票交易所挂牌上市,目前为美国最大规模的P2P借贷平台。2007年国内出现了第一家P2P借贷平台拍拍贷,同年10月宜信借贷平台上线,从2011年开始,国内P2P借贷平台进入快速发展期,伴随而来的则是大量业务乱象。 2016年监管部门对P2P贷款的合规管理开始不断收紧,截至2017年12月底,正常运营的P2P贷款平台数量为1 931家,相对于2016年底减少了517家[3]。
与传统银行贷款不同,P2P贷款完全通过线上完成,属于直接融资的一种,由于缺乏第三方金融中介参与,借贷双方存在很大的信息不对称性,投资人只能独立对贷款未来的违约概率、预期收益等进行预测[4],以期预防投资风险,并获得更高的投资收益。目前由于缺乏有效的P2P贷款违约预测方法和工具,投资人要么简单遵循“大数原则”进行投资分散以规避风险,要么选择利率更高的贷款以期获得风险补偿,这在相当程度上进一步加剧了P2P贷款中的道德风险和逆向选择。
目前对P2P贷款违约预测方法,根据使用的信息来源不同,主要可分为基于借款人信息和基于投资人信息两类。
1 基于借款人信息的P2P贷款违约预测
该类方法基于借款人提供的各类信息,包括年龄、性别、婚否、借款总额、收入负载比、总体负载率等,对贷款的违约概率进行预测。模型主要包括线性回归(Linear Regression, LR)[5]、Logitics回归(Logitics reGression, LG)[6-7]、支持向量机(Support Vector Machine, SVM)[8]、核模型(Kernel-Based Model, KBM)[8]、贝叶斯网络(Bayesian network)[9-10]等,使用最普遍是LR、LG、SVM等模型。
但由于P2P贷款中借贷双方信息不对称性,借款人存在较大道德风险,其提供信息的完整性和真实性很难保证,故基于这些信息所进行预测的准确性也受到较大限制[4,11]。
2 基于投资人信息的P2P贷款违约预测
P2P贷款是多对多的投资方式,即一笔贷款由多名投资人投资,而一名投资人也可以投资多笔贷款,两者之间的关系如图1所示,其中psi、pfi、investi分别是投资人i的投资稳定率、投资收益率和投资贷款数量,Bidi, j和Ratei, j分别为投资人i对贷款j的投资金额和出价利率,debtj是贷款j的投资人数量。
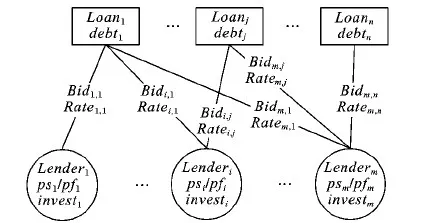
图1 P2P贷款与投资人之间的关联关系Fig. 1 Relationship between P2P loans and lenders
针对借款人提供信息真实性无法得到有效保障的问题,文献[12-14]中提出了基于贷款投资人端信息对P2P贷款违约率进行预测,并取得了较好效果。该预测模型基于投资人稳定性(Lender Stability, LS)保持不变的假设,具体如式(1)所示:
(1)
其中:wi为投资人i的权重因子,其计算方式为投资人对该笔贷款的投资金额Bidi, j占该笔贷款总金额的比例;psi为投资人历史投资稳定率,即其投资中状态为正常的投资金额与其总投资金额的比率;参数normali为投资人i所投资的状态为正常的贷款数量。
LS模型利用投资人端的信息进行贷款违约预测,避免了借款人提供不真实借款信息的道德风险,但其假设投资人所投贷款稳定性趋同的假设,并未考虑P2P贷款之间以及投资人之间的差异性。不同的贷款具有不同利率,即使相同的违约概率也可能带来不同的收益,而不同投资人由于在风险偏好、投资效用、投资能力、所掌握信息等方面存在的差异,也会影响其投资判断和决策。另外,该模型按投资金额比例来计算投资者相对贷款的权重,并未考虑不同投资者以往在投资总量、投资分布等方面的差异。
3 模型设计及算法实现
本文基于投资效用理论,对投资人的投资偏好、投资判断等进行量化定义和测算,提出了基于投资人效用(Lender Utility, LU)的贷款违约预测模型。同时,借鉴信息检索中的词频-逆文本频率(Term Frequency-Inverse Document Frequency, TF-IDF)算法,对投资人与贷款之间的关联权重因子进行优化,以期进一步提升预测准确性。

表1 符号和定义Tab. 1 Symbols and definitions used in this paper
3.1 条件假设
假设1 贷款状态只包括正常(Normal)与违约(Default),不考虑还款延迟(Late)等情况。
假设2 所有贷款为无抵押担保,一旦出现违约,将该笔贷款的总额都记为损失,不考虑已收回还款金额。
假设3 投资者的风险偏好和投资目标是稳定和持续的,投资者将不断学习提升投资能力,以达到自己预期的投资收益。
假设4 投资者是理性的,能充分利用自身知识和掌握的各类信息,作出自身认为最优的投资判断和决策。
假设5 贷款成立前经过充分竞价,即有足够多的投资者提出投资意向,包括投资金额及可接受的最低利率,如果该笔贷款成立,将按照投资者提出的利息报价从低向高逐笔匹配投资金额[1,15]。
3.2 基于投资人效用的贷款违约预测模型
3.2.1 贷款收益率与违约率之间的关系
根据假设1,贷款的违约率与正常率之间满足关系pnj=1-pdj,即预测贷款的违约率与预测其正常率实现了统一。而根据假设2,贷款预期收益率可由预期回报利率减去预期损失率得到,即profitj=rj*pnj-pdj,其中rj是贷款j最终成立时的利率,profitj是该笔贷款的预期收益率。将这两个等式联立,即可以得到贷款收益率与正常率之间的关系。
profitj=(1+rj)*pnj-1
(2)
3.2.2 考虑投资人投资效用的差异性
根据假设3,投资人的投资收益率pfi从长期来看将趋于稳定,可通过其历史投资盈利(正常贷款的利息收益-减去违约贷款损失),与其历史投资总额的比率来计算。
(3)
基于经济学中效用理论,不同投资人有不同的投资偏好,但所有投资人都追求效用最大化,即在承担相同风险时追求投资收益最大化,或是获得相同投资收益时承担最小的风险[16]。根据假设4,投资人会基于自己的投资知识和所掌握的各类信息,对贷款未来是否正常的概率pnj进行预测,然后以自己的投资目标收益率为基线,尽可能地提高利率报价,以期尽可能地获得更高投资收益。
但与此同时,基于假设5,贷款在成立前将经过充分的利率竞价过程,投资者为了投资成功,将不断降低对该笔贷款的利率报价Ratei, j,从而该笔贷款的预期收益率也在不断降低,直到回到投资人的目标投资收益率底线,即profitj=pfi,如果竞争进一步拉低该笔贷款的利率报价,投资人判断预期收益率过低,将放弃投资该笔贷款。最终,该笔贷款的利率报价将实现市场出清(market clearing)[17],即所有投资人只能实现其各自的目标投资收益率,无法获得任何超额收益。
由此,可以借助投资人的历史收益率、贷款利率报价等信息,推算投资人是如何评估某笔贷款的正常概率的,具体方法如式(4)所示:
pfi=profitj=(1+Ratei, j)*pn_bidi, j-1 ⟹
(4)
在式(4)基础上,考虑将贷款所有投资人预测的违约概率进行加权汇总,权重因子依然按照投资金额比例进行计算,可以建立基于投资人效用的P2P贷款违约预测模型,具体如式(5)所示。
(5)
3.3 借助信息检索TF-IDF算法优化投资人权重因子
基于投资人信息的P2P贷款违约预测模型,很关键的一点就是更准确地度量投资人与贷款之间的相关性,即不同投资人的权重计算因子。目前研究中该因子的计算方式比较简单,即依照投资人投入资金的比例来计算投资人对贷款的权重,该方法将所有投资人都等同看待,并未考虑不同投资人在投资总量、投资分布等方面的差异性。
信息检索领域一个比较重要的研究内容就是词语与文章之间关联关系。一篇文章包含了不同的词语,一个词语也可以出现在多篇文章之中,两者关系如图2所示。对比图1和图2可以发现,投资人对P2P贷款进行投资,与词语组成文章的关联关系非常类似,本文考虑借鉴信息检索中比较成熟的技术和算法,以期更好地利用投资人的信息对P2P贷款违约进行预测。
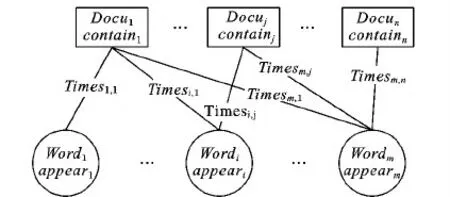
图2 信息检索研究中文章与词语之间的关联关系Fig. 2 Relationship between documents and words in information retrieval research
TF-IDF(Term Frequency-Inverse Document Frequency)是一种信息检索研究中常用的加权算法,其核心思想是字词的重要性随着它在文件中出现的次数成正比增加,但同时会随着它在语料库中出现的频率成反比下降[18-19]。
借鉴TF-IDF算法,本文对投资人相对于贷款的权重因子计算方法进行了优化,在原有的投资占比因子(类TF)基础上,增加投资者的逆向投资比例因子(类IDF),于是在投资人效用的预测模型基础之上,建立了基于TF-IDF算法的P2P贷款违约预测模型,其计算方法如式(6)所示。
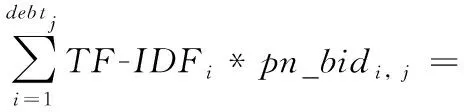
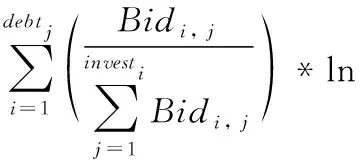
(6)
3.4 主要算法实现
算法1 计算投资人历史投资收益率。
算法说明 遍历投资人所有的历史投资贷款,基于各笔贷款的违约情况、投资金额和利率,根据式(3)计算该投资人的历史投资收益率。
输入 投资人所有贷款的集合Loani。
输出pf。
初始化pf=0,Sum=0,Earning=0。
Fori=1 tondo
Sum=Sum+Loani.BidAmount
//记录投资总额
IfLoani.Status=′Default′ Then
//贷款违约了
Earning=Earn-Loani.BidAmount
//全部投资金额被作为损失从投资盈利中扣减
Else
//贷款状态正常
Earning=Earning+Loani.BidAmount*Loani.Rate
//将投资收益(投资额与利率的乘积)计入投资盈利
End if
End for
pf=Earning/Sum
//计算总的投资收益率
算法2 基于pLU2模型测算贷款正常率。
算法说明 遍历某笔贷款所有的合格投资人(投资数量或投资收益达到一定要求),基于其历史投资收益率、利率出价、历史投资数量等信息,根据式(6)测算该笔贷款的正常概率。
输入 贷款Loan,贷款所有竞价的集合Bidi。
输出Pn。
初始化tf=0,idf=0,Pn′=0,Pn=0。
Fori=1 tondo
IfBidi.LenderStatus=′Qualified′ Then
/*是否为合格投资人,即历史投资数量、历史投资收益率等满足一定要求,设置此条件是为了避免缺乏经验的投资人,因其投资表现波动随机性过大,对预测结果的稳定性产生影响*/
CheckRelativity(Loan,Bidi.Lender)
/*检查当前贷款是否计入投资人的投资历史,如果是则将其从投资人的投资历史中剥离,以防造成预测结果的过拟合*/
tf=Bidi.BidAmount/Loan.Sum
//计算TF权重因子
idf=Ln(Tloan/Bidi.LenderInvest+1)
/*计算IDF权重因子,分母加1的处理,是为了避免首次投资的投资人其投资数量为0的情况*/
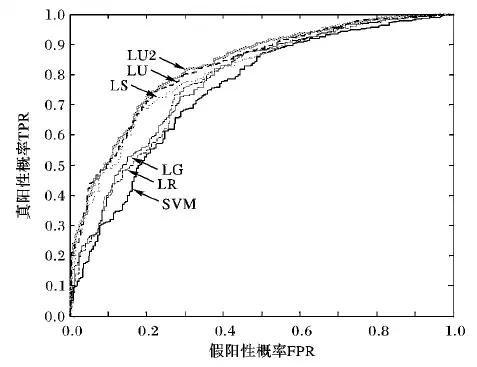
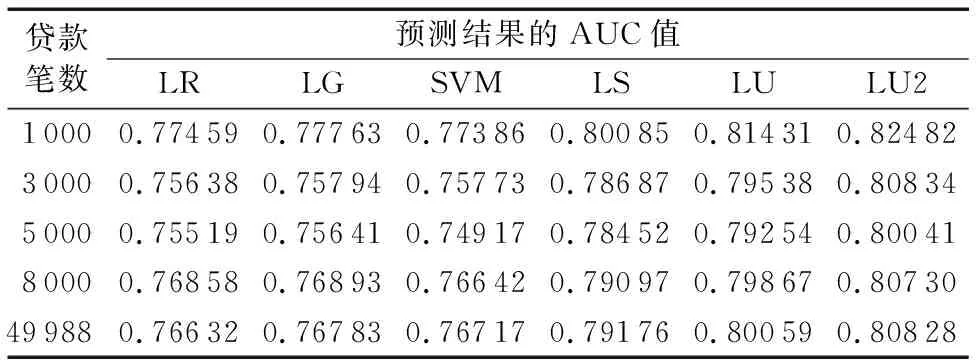
IfBidii.LenderProfit /*如果该投资人历史收益率低于本笔贷款的利率,则推算的概率不高于1*/ Pn′=(1+Bidii.LenderProfit)/(1+Bidi.Rate) /*从投资人效用角度推测的贷款正常预期概率*/ Else Pn′=1 /*如果该投资人历史收益率超过了本笔贷款利率,则进行修正,即推算的概率最高为1*/ End if Pn=Pn+tf*idf*Pn′ //加权汇总所有投资人的预测结果 End if End for 目前国内大部分P2P平台贷款业务数据开放程度相对都不高,尤其是贷款违约情况、投资人投资情况等数据基本不公开。本文使用的实证数据来自美国的P2P借贷平台Prosper.com,除了贷款、借款人、投资者、是否违约等信息外,还包括了贷款竞价(Bid)过程的相关信息(如投资金额、利率出价等),这为验证基于投资人信息的预测模型提供了数据基础[20]。 实验数据中贷款总数量为49 988笔,训练数据集和测试数据集共分为10组,采取放回取样的方式随机进行抽取,训练数据集大小为1 000笔,测试数据集分别为1 000笔、3 000笔、5 000笔、8 000笔和全部贷款。表2是各数据集的平均统计信息,可以发现各数据集中违约贷款的比率基本一致,不存在不平衡情况。 表2 训练数据集与测试数据集的统计信息Tab. 2 Statistics of training datasets and test datasets ROC(Receiver Operating Characteristic)曲线和AUC(Area Under Curve)值常被用来评价一个二值分类器(binary classifier)的优劣。ROC曲线最早运用在军事上,后来逐渐运用到医学领域,再被运用到统计分析研究中,其可准确反映某分析方法特异性和敏感性的关系[21-22]。 ROC曲线以下部分的面积即为AUC,AUC值可以解释为任取一对(正、负)样本,正样本的预测值大于负样本预测值的概率[23]。AUC值越高表示模型预测效果越好,而且其具有一致性和稳定性的特点,即不受判断阈值选择影响,且即使测试集中正负样本分布不平衡,AUC值也能保持稳定,故本文采用AUC值对各模型的预测效果进行比较和分析。 进行验证对比的模型共6种,分别是线性回归(LR)、Logitics回归(LG)、支持向量机(SVM)、基于投资者稳定性(LS)、基于投资者效用(LU)、TF-IDF算法优化后的基于投资者效用(LU2)。 4.3.1 各模型预测结果ROC曲线对比 各模型预测结果的ROC曲线对比见图3,为测试数据集为1 000笔贷款的预测结果,其中:假阳性概率(False Positive Rate, FPR)是指实际违约了的贷款(False)被预测为正常(Positive)的概率;真阳性概率(True Positive Rate,TPR)是指实际正常的贷款(True)被预测为正常(Positive)的概率,即召回率(Recall)。 图3 各模型预测结果的ROC曲线对比Fig. 3 Comparison of ROC curves of prediction results by different models 可以看到实验结果中基于借款人信息预测模型(LR、LG、SVM)的ROC曲线,处于基于投资人信息预测等模型(LS、LU、LU2)ROC曲线的右下部,即在相同TPR值时,前一类预测模型具有更高FPR值,也就是更容易将实际违约的贷款预测为正常,这说明了基于借款人信息的预测模型更容易受到借贷人提供不真实信息影响。而LU2模型预测结果的ROC曲线一直保持在左上区域,这表明该模型预测效果最为理想。 4.3.2 各模型预测结果的AUC值对比 各模型预测结果的AUC值见表3,可以发现基于借款人信息的预测模型表现非常接近(LG比LR稍好,SVM表现最差),但都与基于投资人信息的几个预测模型存在明显的差距。本文提出的基于投资人效用(LU)模型的预测准确性明显较高,而经过TF-IDF算法优化权重后的LU2模型,预测准确率更是进一步提升,这进一步验证了通过投资人的信息进行预测能更有效地避免借贷双方的信息不对称性问题。 表3 各模型预测结果AUC值Tab. 3 AUC values of prediction results by different models 表4是LU2与其他模型在预测准确性方面的比较情况。LU2模型在不同测试数据集上都取得了最好的预测准确性,相对于基于投资人稳定性(LS)模型,LU2模型预测准确性平均提高了2.38%,而相比基于借款人信息的模型(LR、LG、SVM) 更是提高了5.76%至6.16%。 表4 LU2相比其他模型的预测准确性提高比例Tab. 4 Prediction accuracy improvement of LU2 compared to other models P2P贷款的业务模式要求投资者对贷款违约率进行更准确的预测。传统方法是使用线性回归等模型,基于借款人提供的各类信息进行预测,其效果受借贷双方信息不对称性限制。近期相关研究提出了利用贷款投资者端信息进行预测的方法,但并未考虑不同投资人在风险偏好、投资效用、历史投资分布情况等方面的差异。 本文利用来自投资人的投资历史收益率、贷款利率出价等信息,提出了一种基于投资人效用的P2P贷款违约预测模型,并借鉴信息检索领域的TD-IDF算法,构造了投资人逆向投资比例因子,以更准确地量化和度量不同投资人对贷款违约概率预测的计算权重。通过实际P2P贷款数据的实证比较,本文所提模型的预测准确性与其他模型相比表现最优,并且在不同测试数据集上均表现稳定。后续可在通过集成学习方法[24-25]整合基于借款人信息和基于投资人信息的两类模型,以及增加对投资人投资行为动态时序分析等方面开展进一步的研究。4 模型实证结果比较与分析
4.1 实验数据说明

4.2 模型预测效果比较的方法
4.3 实证结果分析

5 结语
