固定密钥与密文长度的访问控制方案
2018-11-22唐忠原何利文焦宏宇
唐忠原,何利文,陈 超,焦宏宇,吴 超,周 睿
(南京邮电大学 计算机学院,江苏 南京 210003)
0 引 言
随着云计算的发展,云安全已成为亟待解决的关键问题,严重制约了云服务的快速发展[1]。目前云服务还存在如下安全问题:(1)云平台的不可信性;用户将数据存储在公有云上,失去了对数据的直接控制,服务器可能会对用户的敏感数据进行窥探、修改等操作,因此严重威胁用户数据的安全;(2)用户身份隐私的保护;只有通过身份认证的用户才有权限对数据进行访问,而常用的认证信息是身份信息,一旦泄露,将会造成用户隐私的泄露[2]。因此要让企业与个人用户大规模地使用云平台,必须着手解决云存储面临的一系列安全问题,目前对数据的访问控制成为解决数据安全的关键技术。
通过访问控制,可以显式地对关键数据的访问进行有效控制,保护用户隐私数据安全。针对云计算面临的安全问题,通过传统的访问控制机制(自主访问控制、强制访问控制等)难以达到完美的效果;所以将数据加密后再上传到云服务器,是保护数据安全的一个重要思路。因此,基于密码学方法和工具实现的访问控制技术是目前的研究热点[2]。
1 国内外研究进展
Shamir和Boneh等提出基于身份的加密机制(identity-based encryption,IBE),通过将用户的私钥与用户的身份关联,以达到对信息的访问控制[3]。基于此,2005年,Sahai和Waters提出了基于模糊身份的加密机制(fuzzy identity-based encryption,FIBE),将用户的身份信息用多个属性来标识,开启了基于属性加密的先河(attribute-based encryption,ABE)[4]。为了实现更加灵活的访问控制策略,2006年,Goyal提出了基于密钥策略的属性加密方案(key-policy attribute-based encryption,KP-ABE)[5],使用文件的描述信息作为属性,实现了对加密数据的细粒度访问。2007年,Benthcourt等提出了基于密文策略的属性加密方案(ciphertext-policy attribute-based encryption,CP-ABE)[6],以用户身份信息作为属性,数据拥有者可以决定数据的访问策略,适合作为云计算环境中的访问控制。文中正是基于CP-ABE加密的访问控制策略。
在传统的基于CP-ABE的访问策略中,密文与密钥的长度依赖于属性的数量,随着属性数量的增加,密钥与密文长度也随之增加,导致系统性能严重下降。文献[7]提出了基于固定密文长度的CP-ABE,该方案采用“与”门限访问结构,但要求访问控制结构中的属性数目与用户私钥保持一致,并且该方案加、解密的计算代价与属性的个数呈线性关系,因此不利于实际应用。文献[8-9]同样使用“与”门的访问结构,提出了固定密文长度与固定计算开销的访问控制方案。但是文献[8]在加密和解密时效率低下,时间复杂度过高。文献[10]为了降低用户的计算开销,进行了大量的预计算,该方案确实可以降低用户的计算量,适合轻量级设备,但是需要大量的可信实体来保存并传送数据,并加重了云服务提供商的计算负担。文献[11]使用LSSS的访问结构,提出了两种不同的CP-ABE策略以适应不同的场景,可以大大降低密文的长度。文献[12]使用一个优化的矩阵来达到固定密文长度。文献[13]基于CP-ABE的加密策略,采用“与”的访问结构,可以实现固定密钥长度,适合应用于轻量级设备的访问控制。文献[14]在文献[13]的基础上实现了固定密文与密钥长度的解决方案,降低了通信开销,但是加解密计算开销量较大的问题仍然没有解决,并且没有涉及用户权限撤销的问题。因此设计一个固定密文与密钥长度,固定的加、解密计算开销并且包含撤销功能的CP-ABE算法仍然是一个具有挑战性的难题。
文中在文献[13-14]的基础上,针对传统CP-ABE加密方案中密文与密钥长度过大,加、解密计算量较大的问题,提出了基于RSA的CP-ABE访问控制策略。使用“与”门的访问结构,在保证密文与密钥固定长度的前提下提高了加解密的计算效率,放弃了传统的双向性映射的计算方式。为了保证属性、密文在传输过程中的完整性,引入了签名方案。并且添加了用户撤销的功能[15],将用户身份标识嵌入密文当中,可以在不实现对密文重新加密与更新密钥的前提下,临时撤销用户的权限,并不影响其他用户的正常使用。
2 模型定义
2.1 属性与访问结构
文中仿照文献[13]的方式来定义属性集与访问结构,定义具有n个属性的属性全集U={A1,A2,…,An}。每一个Visitor作为Owner文件的访问用户,具有的身份信息以属性集V表示,是属性全集U的非空子集(V⊆U)。V用一个n位字符串a1a2…an表示,定义如下:

例如:若n=4,定义一个Visitor的属性集为V={A1,A2,A4},所以Visitor的属性字符串为1101。
定义一个访问策略P,其也为属性全集U的非空子集,P用一个n位字符串b1b2…bn表示;
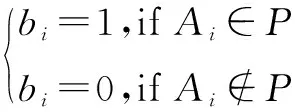
例如:若n=4,访问策略字符串为1010,则访问策略P的属性集为{A1,A3}。
文中使用“与”门的访问策略进行研究。假设Visitor的属性集V的字符串为a1a2…an,访问策略字符串P为b1b2…bn。如果ai≥bi(∀i=1,2,…,n),则P⊆V,则Visitor的属性集V满足访问策略P。
2.2 可计算性理论
(1)整数因子分解难题。
依据RSA算法,选取两个ρ位的大素数p,q,N=pq。GenF是一个以1ρ作为输入、(N,p,q)作为输出的多项式时间算法。由于已知一个大数N,因式分解得到p与q是异常困难的,这也是RSA加密算法安全的根本原因;根据文献[16]中的定义,对于概率多项式时间(PPT)算法T,因式分解的优势可以定义如下:
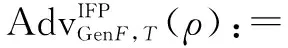
(2)困难性假设。
文中访问控制方案的安全性依赖于Diffie-Hellman假设[17],使用RSA模数N=pq解决Diffie- Hellman模式与基g的问题等同于计算如下函数:
DH(N,g,X,Y):〈g〉N×〈g〉N→〈g〉N
其被定义如下:
DH(N,g,ga,gb)=gab(modN)

定义1:一个t多项式时间算法T,当Z=grd时,输出0,否则输出1;算法T解决n-IF-DH问题的优势定义如下:
2.3 CP-ABE加密策略的定义
文中的CP-ABE的加密策略共包含以下五个算法:
(1)Setup(ρ,U)→(MPK,MSK)。
系统建立算法,算法以安全参数ρ与属性集合U={A1,A2,…,An}作为输入,输出公共参数MPK与系统主密钥MSK,选择一个无法伪造的签名方案生成签名密钥Signkey和验证密钥Verifykey。
(2)Encrypt(P,MPK,M,Rev)→(C)。
加密算法,算法使用E[P,M,MPK,Rev]加密算法将访问策略P、公共参数MPK、明文M与用户撤销列表Rev加密,输出密文C。
(3)KeyGen(A,MPK,MSK,T)→(SKuor ⊥)。
密钥生成算法,当Visitor访问CA请求私钥时,CA运行该算法;算法以Visitor属性集V、公共参数MPK、系统主密钥MSK以及过期标志T作为输入,如果Visitor合法,生成用户的密钥SKu;否则输出⊥。
(4)Decrypt(C,P,MPK,SKu,GID)→(Mor ⊥)。
该算法根据密文C、访问策略P、公共参数MPK、用户私钥SKu以及用户标识GID,如果P⊆A,并且GID∉Rev,则可解密得到明文M,否则得到⊥。
(5)Revoke(FID,GID)→(C)。
用户权限撤销算法,Owner将二元组(FID,GID)发送给CS,CS根据FID查找相应的文件密文C,并将GID写入文件密文C的Rev集合中。
2.4 系统模型
系统模型如图1所示,主要包含以下四个实体:
Owner:是一个数据拥有者,定义数据的访问控制结构,对数据进行加密并上传云服务器,同时拥有撤销用户访问共享文件的权限。
CS:是云存储服务器,是一个半可信的数据存储结构,同时提供数据访问服务;但它会对Owner的数据保持好奇,并猜测其中内容。
CA:是一个可信的授权机构,负责生成系统的公共参数MPK与系统主密钥MSK,同时会根据用户的访问请求与属性集生成私钥并发送给用户。
Visitor:是数据的使用者,当其拥有的属性值集合满足访问控制结构时才能成功下载并解密密文。
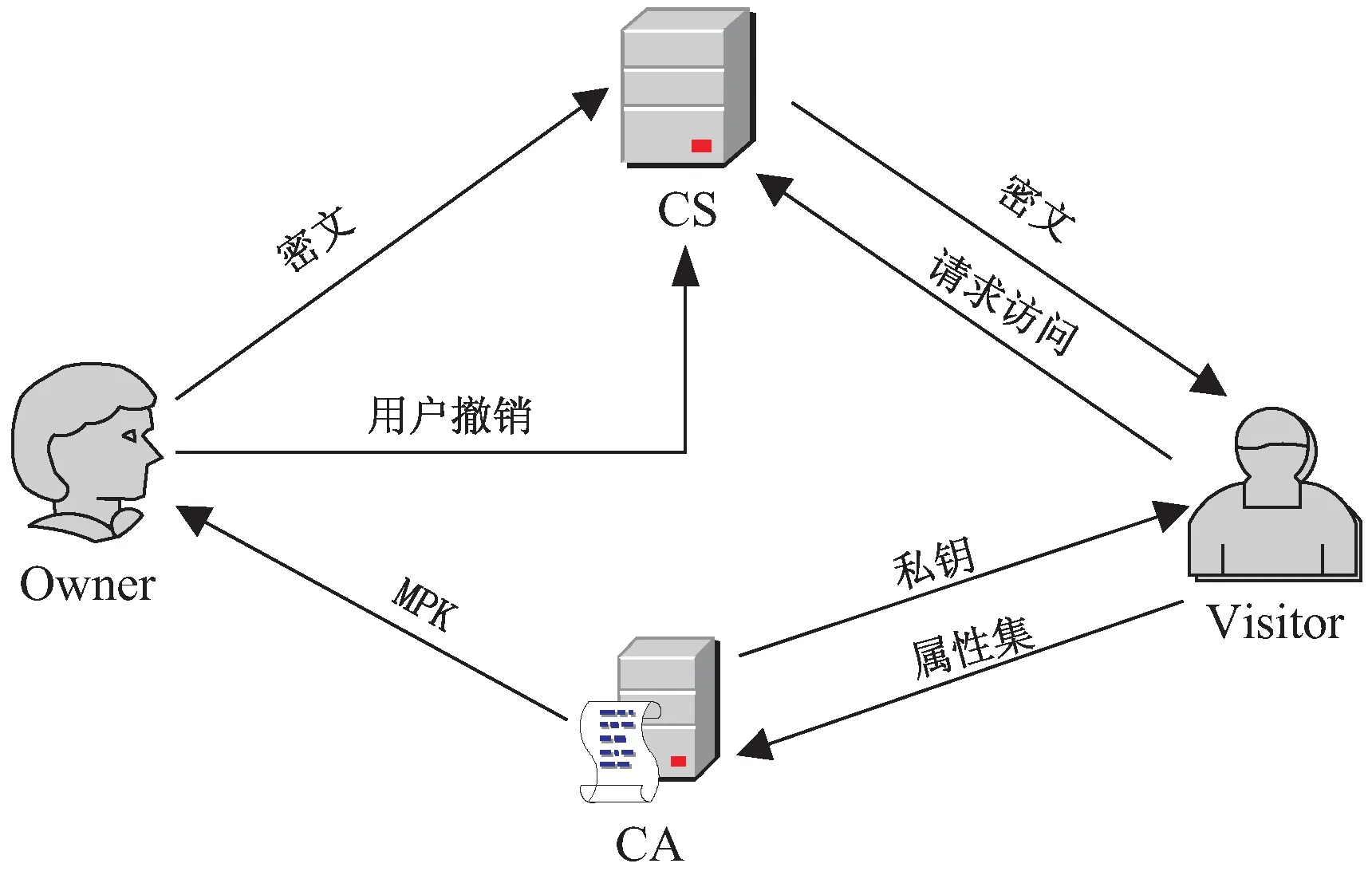
图1 系统模型
2.5 安全模型
文中通过一个敌手与挑战者之间的游戏来验证系统的安全性,其定义如下:
(1)初始化阶段:敌手A输出想要挑战的n位访问控制策略P,并将其发送给挑战者B。B使用安全参数ρ运行Setup与KeyGen算法,得到(MSK,MPK),并将MPK发送给A。
(2)查询阶段1:敌手A开始向挑战者B进行如下查询:
敌手A进行多次提交其属性集Vi向挑战者B进行查询,但是属性集都不满足访问结构Pi,即Pi⊄Vi。挑战者B运行KeyGen算法,并将生成的密钥SKi发送给敌手A。
敌手A对被E[Pi,Mi]加密的密文进行解密查询。
(3)挑战阶段:敌手A提交两个长度相同的明文(M0,M1)且M0≠M1;挑战者取一个随机值c∈{0,1},并运行加密算法E[P,M]输出密文C发送给敌手A。
(4)查询阶段2:敌手可以继续进行密钥查询与解密查询,但是属性集Vi不满足访问结构Pi;继续执行,同查询阶段1。
在该游戏中,敌手A赢得游戏的优势ξ定义如下:
2.6 定义访问结构中的密钥管理
该部分将密钥管理融入到访问结构当中,根据RSA加密原理,因式分解N=pq是一个可计算的难题,因此在不知道安全参数p与q的值的前提下计算φ(N)=(p-1)(q-1)也基本不可能。据此,选取安全的素数pi(∀i=1,2,…,n),满足gcd(pi,φ(N))=1;然后计算qi,满足piqi≡1 (modφ(N)),其中如果i≠j则pi≠pj。因此可以使用整数因式分解难题来保存与公开素数pi相关的qi;所以将{φ(N),q1,…,qn}作为秘密参数,则{N,p1,…,pn}是公开参数。
选取一个随机数g(2 KV=gdV(modN) KP=gdP(modN) 另一方面,如果P⊆V,则KP计算如下: 文中使用的所有符号及定义如表1所示。 表1 符号的定义 输入用户的安全参数ρ与属性集合U={A1,A2,…,An}。 Step1:CA执行Setup函数,使用一个无法伪造的签名方案,生成签名密钥Signkey和验证密钥Verifykey。合法的Visitor注册时,需要向CA提交自己的属性,CA为该Visitor生成一个全局唯一的标识符GID与一个时间过期标志T,使用Signkey签名后生成标签flag(GID,A,T),发送给Visitor。 Step2:根据RSA算法,来选择两个大素数p、q(p≠q),N=pq;然后随机选择Pi,并且Pi与φ(N)互质;再计算与属性Ai(∀i=1,2,…,n)相关的Qi,PiQi≡1 (modφ(N))。接着选择系统的私有密钥对k、x,满足gcd(k,φ(N))=1,gcd(k,Qi)=1,gcd(x,Qi)=1(∀i=1,2,…,n)。最后选择一个随机数g,满足2 Step3:选择三个抗碰撞hash函数H1,H2,H3,定义如下: H1:{0,1}*→{0,1}ρ H2:{0,1}*→{0,1}lσ H3:{0,1}*→{0,1}lm 其中,lσ为安全参数随机字符串的长度;lm为明文信息M的长度。 Step5:输出系统主密钥MSK与公共参数MPK: MPK={N,DU,Y,R,H1,H2,H3,P1,…,Pn,Signkey} Owner将数据上传到CS共享之前,首先进行加密,该方案基于文献[12]的加密方案,使用MPK、M与R作为输入,加密计算经过如下阶段: Step1:Owner为每个文件生成唯一的标识符FID,用于标识各个文件。并为每个文件生成一个用户撤销列表Rev,用于临时保存被Owner撤销的用户GID。 Step3:为了保证明文的有效性,计算签名Sm=H1(σm)⊕M,并计算Ym=gxrm,Rm=gkrm,使用σm对明文M加密,Cm=H3(σm)⊕M。 最后输出密文:C={FID,P,Rev,Ym,Rm,Cσm,Cm,Sm},并将加密好的密文发送到CS。 Step1:Visitor请求访问数据,首先将自己的标签信息flag(GID,A,T)发送到CA,CA通过Verifykey验证用户是否合法,如果合法,并且Visitor的身份信息T在有效期内,则进行下一步,否则输出⊥。 Step3:选取两个随机数ru与tu,通过dV=ksu+rux(modφ(N))计算su,然后计算k1=su+xtu(modφ(N))与k2=ru-ktu(modφ(N))。 最后输出用户密钥SK=(GID,k1,k2)。 Visitor想要访问某个文件时,将自己的标签信息flag(GID,A,T)发送给CS,CS判断用户信息是否在有效期内,并判断GID是否在访问文件密文的Rev列表中,如果用户信息在有效期内且用户权限没有被撤销,则CS将该文件密文发送给Visitor。Visitor经过以下步骤进行解密。 Step1:为了保证密文不被撤销的用户解密,再次查看密文C中的Rev中是否包含GID,如果包含,则无法解密,否则进入下一步。 如果数据Owner想要临时撤销某个Visitor对某个共享文件的访问,向CS提交二元组(FID,GID),CS根据该二元组找到对应的文件,并将GID添加到该密文C中的Rev中。被添加到Rev中的文件将无法被下载与解密。 定理1:该策略可以抵挡敌手对系统私钥对(k,x)的碰撞攻击。 (1) (2) 在密钥生成阶段有: dVi=k·sui+rui·x(modφ(N)) (3) 由以上式得,如果sui与tui是已知的,可以得到唯一的(k,x)的解;然而,由等式1与2分别形成的l个线性等式中有2l+1个未知数,即等式1需要猜测(sui,tui)的值才能解出x,等式2也需要猜测(rui,tui)的值才能解出k的值。由于sui与rui对敌手来说是两个未知的随机数对;因此,敌手根据自己的私钥对SKi是无法合谋得到系统私钥(k,x)的。 定理2:该策略可以抵挡敌手根据属性集V获得有效用户私钥SK=(GID,k1,k2)。 证明:由定理1可得,敌手A无法通过合谋碰撞攻击获取系统的私钥对(k,x),因此也无法获取中间变量su,因为根据dV=ksu+rux(modφ(N))求解su类似于RSA中求p与q。因此在不知道(k,x)与su的前提下,即使敌手可以自己随机选取ru与tu,也无法获得用户密钥SKu=(GID,k1,k2),因为它依赖复杂的欧拉函数φ(n)=(p-1)(q-1)。 定理3:由于整数因式分解问题是密码学难题,所以该策略可以抵挡敌手根据用户属性V(P⊄V),获取其相关的密文C={FID,P,Rev,Ym,Rm,Cσm,Cm,Sm}相关的关键中间变量Km,因此敌手无法解密密文。 证明:由解密公式得: 如果P⊄V,由命题1得,将无法计算Km,在不知道Km的前提下,无法计算密文。因此,该方案可以抵挡未授权的用户解密密文。 定理4:由于DH问题的难解性,该策略可以抵挡多个未授权用户合谋攻击。 其中,C=A∩B。由于解决DH问题如同解决RSA的模数问题,所以该策略可以抵挡多用户的合谋攻击。 下面给出文中方案与文献[13-14]中的方案在通信、存储与计算方面的性能比较与分析。通常,通信开销指的是密文长度,存储开销指的是密钥长度。由表2可知,存储开销三种方案是相同的;但是通信开销中,文中方案要优于文献[13],即文中方案的密文长度不随属性的增加而增加;并且文中方案支持用户的临时撤销,可以很好地解决撤销用户而频繁进行重新加密对称密钥或者需要重新加密原始数据的问题,大大降低了系统开销,可以很好地应用于实际的开发环境。 表2 通信与存储方面的对比 其中,L为明文M的长度;G与Gt均为素数阶配对群。 同时,为了更好地验证文中方案在加密、解密方面的优势,与文献[13-14]的方案进行对比,进行仿真实验;实验环境为Intel(R) Core(TM) i5 6300HQ处理器,主频2.3 GHz,8 G内存,操作系统为Ubuntu 14.04,算法基于cpabe库使用C++实现。该实验使用的属性个数|U|=1 000,访问策略中属性个数|P|=500,用户Visitor拥有的属性个数|V|=600。 表3展示的是文中方案与文献[13-14]方案的对比。文中方案的加密与解密耗时都为2 ms,因为文中方案放弃了复杂的双向性运算,大大降低了算法加解密的计算时间。 表3 加解密的计算开销对比 ms 在CP-ABE加密散发的基础上,提出了基于固定密钥与密文策略的访问控制方案,实现了固定密钥与密文长度,提高了算法加解密的计算开销与密文密钥的存储开销。该方案还引入了用户实时撤销的功能,在不使用代理重新加密密文与更新密钥的前提下,临时撤销用户私钥的权限,并且不影响其他用户的正常使用;该方案对用户私钥添加了过期函数,如果达到过期函数,则私钥作废需要重新申请私钥,来保证系统的安全。通过理论分析,该方案可以有效抵挡合谋攻击与选择密文攻击。目前,文中暂没考虑属性撤销等问题,如何将属性撤销机制融入到该访问控制方案中是下一步将要考虑的问题。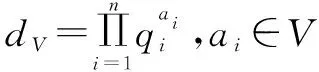

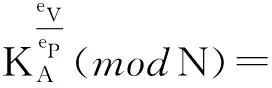
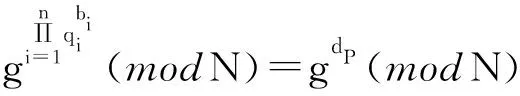
2.7 符号使用与定义

3 模型设计
3.1 系统初始化
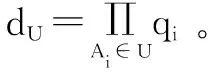
3.2 加密阶段
3.3 密钥生成阶段
3.4 解密阶段



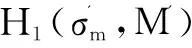
3.5 用户撤销
4 方案的可扩展性与安全性分析
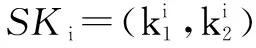
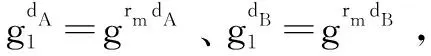
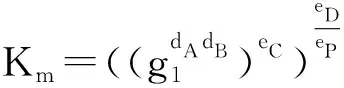
5 性能比较


6 结束语
