Numerical Investigation on a Dual-jet Consisting of a Plane Wall Jet and a Parallel Offset Jet at Low-Reynolds Number

,

1. School of Marine Sciences, Nanjing University of Information Science & Technology, Nanjing 210044, P. R.China;2. College of Aerospace Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, P. R. China

Abstract: A dual-jet consisting of a wall jet and an offset jet has been numerically simulated using lattice Boltzmann method to examine the effects of jet spacing between two jet centerlines, defined as s. The Reynolds number based on jet-exit-width d is set to be Re = 56 and the jet spacing is set to be less than or equal 10 times the jet-exit-width. Computational results reveal that the flow field displays periodic vortex shedding when the jet spacing is in the range of 9 ≤ s/d ≤ 10, while it remains steady with two counter-rotating vortices in the converging region when s/d ≤ 8. When s/d = 9, the power spectral analyses indicate that the vortex shedding phenomenon has specific frequency. The significant oscillation stresses induced by the periodic components of velocities are found to mainly exist in the inner shear layer regions, implying stronger momentum transfer occuring in these regions.

Key words: dual-jet; low-Reynolds number; lattice Boltzmann method; vortex shedding

0 Introduction

Jets are important in a variety of engineering applications, such as entrainment and mixing processes in microcircuit cooling system, ventilation system, waste disposal, and fuel injection systems[1-4]. Besides free parallel jets, the combinated wall and offset jets are also frequently encountered in many industrial processes especially in the wastewater evacuation process which makes interesting to study the dynamic characteristics of this type of flow. The combinated wall and offset jets flow consist of a lower wall jet and a upper offset jet. The lower wall jet is generated when a flow is injected into a region near the wall with an initial momentum. The upper offset jet refers to a flow issuing above a wall which is parallel to the axis of the jet. When the height of the offset is zero, the offset jet will become a wall jet.

A schematic diagram of the combinated wall and offset jets, as modified from previous studies on free parallel plane jets[5], is shown in Fig.1. The origin of the coordinate system is set at the intersection of the jet exit plane and the bottom wall, wherexis along the wall. The two jets, having the same widthd, are separated in the vertical (y) direction by a distance,s. As shown in Fig.1, there exist three distinct regions, a converging region, a merging region and a combined region. A sub-atmospheric pressure zone close to the nozzle plate causes the individual jets to curve towards each other in a region known as the converging region. The two jets merge together at some downstream position (xmp,ymp), known as the merging point which is characterised by the point where velocity is zero. Downstream from the merging point in the merging region, the two jets continue to interact with each other up to the combined point (xcp,ycp), where the deflection point originally in the mid-part of streamwise velocity profile disappears. Downstream from the point in the combined region, the two jets combine to behave like a single wall jet.

Fig.1 Schematic of combinated wall and offset jet(s is the spacing between two jet centerlines, d the jet-exit-width, and Uo the jet-exit-velocity)

combined Wang et al.[6]have experimentally studied the flow characteristics of the combinated wall and offset jets for a Reynolds numberRe= 10 000 and an offset ratios/d= 2. Results revealed that the near filed of the dual-jet flow is characterized by periodic Karman-like vortex street in the inner shear layer regions. The existence of the vortex shedding phenomenon results in periodic interaction between the wall jet and the offset jet. Kumar et al.[7]have numerically studied the flow characteristics of the combinated wall and offset jets for a ralatively larger value of offset ratios/d= 9 whenRe= 20 000. Their results focused on the mean flow and turbulence characteristics of the combinated dual-jet. However, no vortex shedding phenomenon was reported in this paper. Later on, Li et al.[8]numerically investigated the interaction between the plane wall jet and the parallel offset jet besed on large eddy simulation (LES). The considered Reynolds number and the offset ratio were the same as that of Wang and Tan[6]. By means of statistical analysis, they have characterized the interaction between the two jets. The results also included mixing characteristics of the two jets and were in good agreement with the experimental results of Wang and Tan[6], but did not contain any information relating to the vortex shedding phenomenon. In another paper, Li et al.[9]studied the interaction between a wall jet and an offset jet with different velocity and offset ratio using several turbulence models. Similarily, they presented only the steady state results and no vortex shedding phenomenon was reported.

In the study of Mondal et al.[10], the effect of offset ratio on the flow states was investigated whenRe= 10 000 and 1.5 ≤s/d≤ 3.5. Results showed that whens/dlies in the range 1.7≤s/d≤ 3.1, the near field of the flow domain is characterized by a periodic large scale vortex shedding phenomenon. Howerer, outside this range, two steady counter rotating vortices appear in this flow zone. Mondal et al.[11]numerically investigated the effect of velocity ratio (Ur) between the inlet velocity of the wall jet (Uw) and the inlet velcity of the offset jet (Uo) on the unsteady flow structure of this type of flow. Results showed that when the velocity ratio lies in the range 0.78 ≤Ur≤ 1.34, a periodic vortex shedding phenomenon occurs close to the nozzle plate. On the contrary, this periodic phenomenon ceases ifUr≤ 0.77 andUr≥ 1.35. When the velocity ratio is set to 0.77 and 1.35, two stable counter rotating vortices appear in the wall vicinity along the converging zone. Recently, Mondal et al.[12]numerically investigated the effect of the bottom wall proximity on the unsteady flow state of the two jets. Here, the unsteady periodic vortex shedding phenomenon and steady state with two counter-rotating vortices were respectively observed in the flow filed.

According to the literature survey on the area of combinated wall jet and offset jet flow, only few studies[6, 10-12]report vortex shedding phenomenton. It has been reported that periodic oscillation of dual-jet can cause enhanced mixing between the jets with the ambient and has the advantages of both passive and active mixing control[1]. The literature above mainly focused on high-Reynolds number parallel plane jets, i.e.Re> 103. However, in microelectronic cooling systems, the air velocities are small, hence, low-Reynolds number jets are more relevant. However, low-Reynolds numbers combinated wall jet and offset jet flow (i.e.Re< 102) has not been well documented in the literature. The present study is an attempt to investigate the flow characteristics of this type of flow at low-Reynolds number. The periodic vortex shedding phenomenon is also examined based on the instantaneous flow field. More in-depth study on low-Reynolds number combinated dual jet is also useful to provide improved fundamental understanding of the jet stability and transition to turbulence. In most numerical solvers, the flow field is obtained by solving the Navier-Stokes equations. As an alternative computational technique to Navier-Stokes equations, the lattice Boltzmann method (LBM)[13]is employed to investigate the dual jets. The simulation methodology is described in Section 1. The mean flow characteristics of the dual jets are examined. The instantaneous vortex structures are visualized, which displays the existence of periodic vortex shedding, followed by a quantitative analysis of oscillation frequency.

1 Simulation Methodology

Fig.2 Sketch of computational domain

1.1 Governing equations and boundary conditions

The governing equations of the jet flow are incompressible Navier-Stokes (N-S) equations, shown as

(1)

(2)

whereuiis the velocity,pthe pressure field,νthe kinematic viscosity, andxithe spatial coordinate. The subscriptsiandjrepresent the spatial directions.

At each jet exit, a fully developed parabolic velocity profile is prescribed as

(3)

On the free boundaries, as shown in Fig.2, the pressure is prescribed as the ambient pressurep∞and the other variables are extrapolated from the interior solution, allowing for entrainment. A convective boundary condition[14]is adopted at outlet boundary, shown as

(4)

(5)

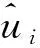
(6)

where constantsαandβare used to control the maximum damping parameter and the exponential growth rate, respectively. For the present study,α=0.001 andβ=3 are used.

1.2 Lattice Boltzmann method

The lattice Boltzmann method (LBM) is employed to solve the N-S Eqs.(1) and (5) in the present work. The fringe functions in Eq.(5) is dealt as an artificial body force[18]acting on the traditional N-S Equation. The lattice Boltzmann equation with the single-relaxation-time BGK approximation and the force term can be written as

fα(x+eαΔt,t+Δt)-fα(x,t)=

(7)

(8)

The force termFαin Eq.(7) is[18]

(9)

(10)

whereρandu=(u,v) are the fluid density and velocity vector, respectively, which can be obtained by the distribution function

(11)

(12)

Through the Chapman-Enskog procedure, the macroscopic N-S Eqs.(1),(5) can be derived from the above lattice Boltzmann BGK model in Eq. (7) and the kinematic viscosity is related to the relaxation timeτ

(13)

1.3 Validation

There was little experimental study on combinated wall jet and offset jet flow at low-Reynolds numbers (i.e.Re< 102) in the literature. However, there are a few experimental studies on single plane jet at low-Reynolds numbers[20, 21]. Therefore, the measurements of single plane jet atRe= 42 by Sato et al.[20]are used as a reference to verify the present computational procedure. Fig.3 shows the mean streamwise velocity 〈u〉 distribution of a single plane jet whenRe= 42. As expected, the velocity on the centerline of the jet decreases and the width of the jet increases downstream. It is observed that the numerical results are in agreement with the experimental data[20], which also validates the reliability of the present work.

Fig.3 Mean streamwise velocity comparing with the experimental data [20] of a single plane jet when Re = 42

2 Results and Discussion

2.1 Mean flow characteristics

The combinated wall and offset jets are kept at a spacing ranges/d≤ 10 for this study and the Reynolds number considered here is 56. The mean velocity distribution illustrates the spatial development of the flow field. Fig.4 shows the mean velocity magnitude contours and streamlines for different offset ratios/d= 6, 8, 9 and 10. The velocity is normalized with respect to the maximum jet-exit-velocityUoc. As seen from Fig.4, each converging region is characterized by a recirculation flow, inside which two counter-rotating vortices are genenrated. The upper offset jet and lower wall jet merge together at merging point (mp), which is characterised by the point where velocity is zero. Downstream from the merging point, the two jets continue to interact with each other up to the combined point (cp). Downstream from the combined point, the two jets combine to behave like a single wall jet.

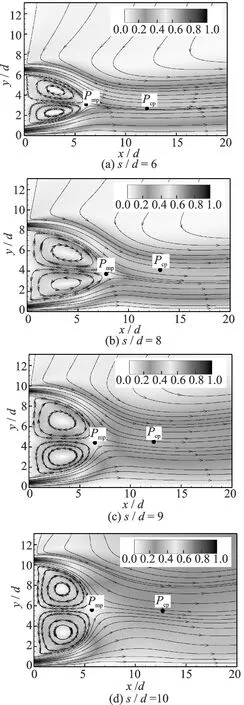
Fig.4 Streamlines and mean velocity magnitude contours for different offset ratio

To see clearly the velocity profile along streamwise section, Fig.5 shows the mean streamwise velocity profile fors/d= 9. The velocity is normalized with respect to the maximum jet-exit-velocityUoc, while theycoordinate is normalized with jet-exit-widthd. As seen in Fig.5(a), in the converging region (x/d< 6.5), the maximum velocity of the offset jet decreases and the jet width increases with the increase in the streamwise distance from the offset plate. In the region surrounded by two jets, there is a recirculation zone where the velocity is negative. The negative velocity becomes positive after the merge point (6.5d, 4.4d). Downstream from the merging point, the two jets continue to interact with each other up to the combined point (12.3d, 4.5d), where the deflection point originally in the mid-part of streamwise velocity profile disappears. Downstream from the combined point, the two jets combine to behave like a single wall jet, as shown in Fig.5(b).

Fig.5 Mean streamwise velocity distributions for s/d = 9

2.2 Instantaneous vortex structures

Fig.6 Instantaneous vorticity contours of the combinated offset and wall jet for different jet spacing s/d at t = 3 000d/Uoc

To demonstrate the unsteady interation process between shear layers, Fig.7 illustrates the instantaneous vorticity contours during a time periodTat an interval ofT/4. Note that the starting time in Fig.7 is arbitrary. As depicted, the discrete vortices are formed in the converging region of two jets. Within time periodT, an upper row of negative vortices (noted asA) and a lower row of positive vortices (noted asB) are alternately grow, shed and convected downstream forming a well-organized vortex street. From Fig.7(a) to Fig.7(c), the upper negative vortexAis seen to grow in size and strength before it becomes strong enough to cut off the lower positive vortexBto shed downstream atT/2. Similarly, from Fig.7(c) to Fig.7(e), the lower positive vortexBis seen to grow in size and strength before it becomes strong enough to cut off the upper negative vortexAto shed atT. In the successive time periods, this phenomenon repeats itself generating the alternate shedding of vortices.

Fig.7 Instantaneous vorticity contours for s/d = 9 at different instants within one time period

2.3 Instantaneous velocity and oscillation frequency

From the above anaylyses, it can be seen that there exist two flow patterns for the combinated wall and offset jets. When the jet spacing is in the range of 9 ≤s/d≤ 10, the flow field displays periodic vortex shedding, while it remains steady with two counter-rotating vortices in the converging region whens/d≤ 8. To capture the unsteady variation of the two flow patterns, the time histories of streamwise (u) and transverse (v) velocities are recorded at two stationary points. For the present study, the stationary points are chosen at PointA(2d, 2d) in the converging region and PointB(15d, 2d) in the combined region. Figs.8(a),(b) shows the time series ofuandvvelocity components at PointAandBfors/d= 8. It can be seen that both velocities remain constant, indicating a steady state behavior. Fors/d= 9, Figs.9(a),(b) shows the time series ofuandvvelocities at PointsAandB, respectively. It can be seen that all velocities exhibit periodic oscillations due to the interaction between inner shear layers. To obtain the frequency of the oscillation, the power spectral densities (PSDs) of velcoities at PointsAandBare shown in Figs.10(a),(b). The non-dimensional characteristic frequency is defined asSt=fd/Uoc, wherefis the dimensional oscillation frequency. For PointAand PointB, as shown in Figs.10(a),(b), bothu-velocity andv-velocity have the same characteristic frequency,Stu,v= 0.012, indicating the frequency of vortex shedding.

Fig.8 Time series of u and v when s/d = 8

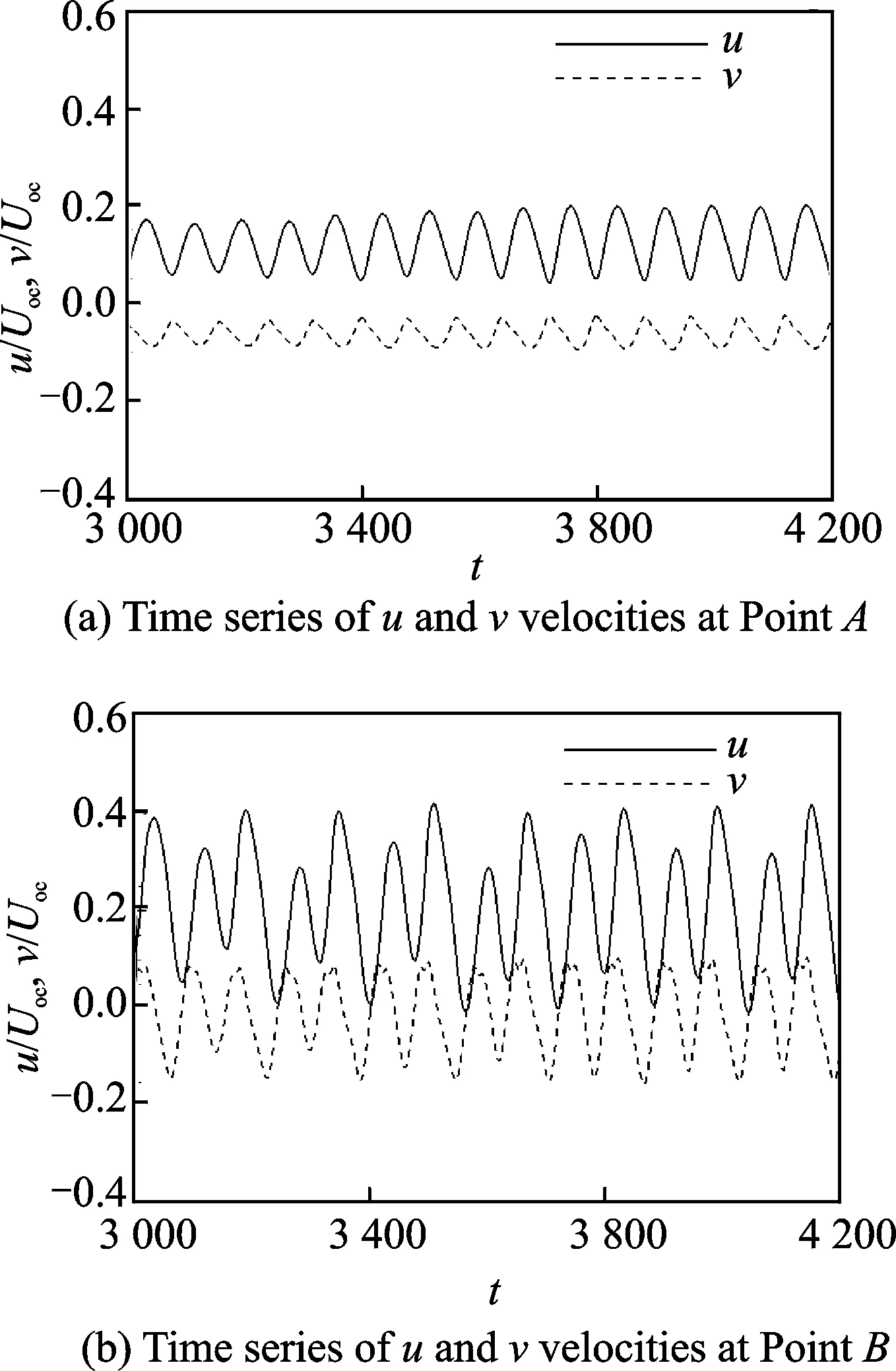
Fig．9 Time series of u and v when s/d = 9

Fig.10 PSDs of velocities exhibited in Fig.9

From the above analyses on velocity components, we can see that there exists periodic oscillation phenomenon in the flow field. If the velocities exhibit periodic components, it could be decomposed as

(14)

(15)

Fig.11 Contour plots of the oscillation stresses

To quantify the effect of the periodic oscillation on the flow field, Table 1 presents the location of merging point and combined point. Whens/d≤ 8, the streamwise distance of merging point and combined point from the nozzle plate are found to increase with increasings/d, which is also noted by others[10, 23]. However, whens/d=9, there exists an apparently decrease for the streamwise distance of both the merging point and combined point, which indicates the merging process starts at a shorter downstream distance fors/d= 9 than that in the case ofs/d= 8. Meanwhile, the combinated jets fors/d= 9 requires shorter distance than that ofs/d= 8 for complete merging to occur. This is attributed to the existence of periodic oscillation, where strong momentum transfer occurs in the converging region whens/d= 9. For the flow field, as the increase ofs/d, there exist two distinguishing flow states. When 9 ≤s/d≤ 10, the flow field displays periodic vortex shedding, while it remains steady with two counter-rotating vortices in the converging region whens/d≤ 8. The transition from steady state to periodic oscillation state ass/dis varied is worthy examination both in studying the approach to turbulence and in its own right.

Table 1 Location of merging point and combined point for different offset ratio

3 Conclusions

The flow features of low-Reynolds number dual jet consisting of a plane wall jet and a parallel offset jet are investigated fors/d≤ 10 using lattice Boltzmann method. The Reynolds number based on jet-exit-widthdis set to be 56. The mean flow in the converging region is characterized by a recirculation flow, inside which two counter-rotating vortices are genenrated. The mean features in the combined region resemble a single wall jet. The instantaneous vorticity contours indicate that when 9 ≤s/d≤ 10, the flow field displays periodic vortex shedding, while it remains steady with two counter-rotating vortices in the converging region whens/d≤ 8. Whens/d= 9, the non-dimensional periodic oscillation frequency (Strouhal number) is found to be 0.012, indicating the frequency of vortex shedding. Fors/d≤ 8, the streamwise distances of the merging point and the combined point from the nozzle plate are found to increase with increasings/d. Whens/d= 9, there exists an apparent decrease for both the merging point and the combined point, which indicates that the merging process starts at a shorter downstream distance fors/d= 9 than that in the case ofs/d= 8. Meanwhile, the twin jets fors/d= 9 require shorter distance than that in the case ofs/d= 8 for complete merging to occur.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (No.11402124), the Natural Science Foundation of Jiangsu Province (No.BK20140985), the Natural Science Foundation of Jiangsu Higher Education Institutions of China (No.14KJB130002), and the Startup Foundation for Introducing Talent of NUIST (No.2013x031).