Two Classes of Quaternary Codes from 4-valued Quadratic Forms
2018-11-21,
,
1.College of Mathematics, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, P.R. China;2.College of Electronic and Information Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, P.R. China
Abstract: Let R=GR(4,m) be a Galois ring with Teichmuller set Tm and Trm be the trace function from R to 4. In this paper, two classes of quaternary codes C1={c(a,b): where and C2={c(a,b):a∈R,b∈Tm}, where c(a,b)=(Trm(ax+2bx2k+1))x∈Tm, and is even, are investigated, respectively. The Lee weight distributions, Hamming weight distributions and complete weight distributions of the codes are completely given.
Key words: Galois ring; quaternary code; Hamming weight; quadratic form; Lee weight
0 Introduction
Codes over rings were first introduced by Nechaev[1]and later Hammons[2]at the beginning of the 1990’s. Since then, codes over rings have been widely investigated[3-10].
Now we recall the definition of quaternary code over4.



Definition0.2LetCbe a quaternary code over4and letA(N0,N1,N2,N3) be the number of codewordsc∈Cwith comp(c)=(N0,N1,N2,N3). Then the complete weight enumerator ofCis the polynomial
whereB={comp(c):c∈C}, the sequence (A(N0,N1,N2,N3))(N0,N1,N2,N3)∈Bis called thecomplete weight distribution ofC. As far as we know, there are few papers which gave the complete weight enumerators of linear codes over rings.
Recently, some quaternary codes are constructed derived from4-valued quadratic forms. In Ref.[11],4-valued quadratic form was introduced by Brown for the first time. Then Schmidt[12-13]gave the basic theories of4-valued quadratic forms. He also constructed a class of quaternary sequences based on4-valued quadratic forms. Letm,kbe positive integers with gcd(m,k)=d, a class of an interesting exponential sum over Galois ring is
a∈R,b∈Tm
whereR=GR(4,m) is a Galois ring with Teichmuller setTmandTrmis the trace function fromRto4. This class of exponential sum is related to a4-valued quadratic forQ(x)=Trm(ax+2bx2k+1). We have some well-known results aboutρ(a,b) as follows:
(1) Fork=1, the distribution[6]ofρ(a,b) was studied to determine the correlation distribution of a quaternary sequence family.
(2) For oddmand gcd(m,k)=1, codes with the same weight distribution as the Goethals codes and Delsarte-Goethals codes[14]were obtained based onρ(a,b).
(3) For oddmandk=1, the theory of4-valued quadratic forms[15]was used to analyze the exponential sumρ(a,b) and new sequence families were obtained.

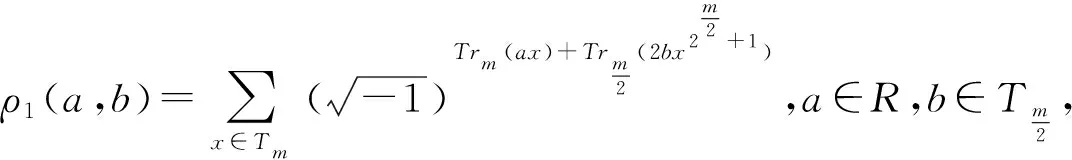
1 Preliminaries
Throughout this paper, we adopt the following notation unless otherwise stated.
Rmthe Galois ringGR(4,m);
Tmthe Teichmuller representative set ofRm;
trmthe trace function fromTmto2;
Trmthe trace function fromRmto4;

Re(x) the real part ofx;
Im(x) the imaginary part ofx.
1.1 Galois rings
Some preliminaries about Galois rings are given below.
For positive integersm≥1, let4be the ring of integers modulo 4 andfa monic basic irreducible polynomial of degreemin4[x]. The ringRm=4[x]/(f) is called the Galois ring, which is a Galois extension of the ring4and denoted byRm=GR(4,m), whereRmis a finite chain ring of length 3 and its unique maximal ideal is 2Rm, i.e. {0}=4Rm<2Rm The Frobenius automorphismσonTmis given byσ(x)=x2. The trace functionstrm:Tm→2andTrm:Rm→4are defined as One can easily check thattrm(σ(x))=trm(x) and 2Trm(x)=2trm(x) hold for allx∈Tm. For more information about Galois rings, readers can refer to Refs.[3,13]. One can easily deduce the following lemma. Lemma1.1Lettrdenote the trace function from2mto2andTrmdenote the trace function fromRmto4. Letμbe the reduction modulo 2. Then Fig.1 shows the communities. Fig.1 Schematic diagram of trace function The proof is obvious,so we omit it here. In the following, we present some results about4-valued quadratic forms[11,13,16]. LetK:={z∈4:z2=z} be the Teichmuller representatives in4. Informally, we identifyKas2={0,1}, which is a subset of4, in this paper. Definition1.2A symmetric bilinear form onTmis a mappingB:Tm×Tm→Kwith two properties: (1) Symmetry:B(x,y)=B(y,x); (2) Bilinearity: for anyα,β∈K,B(αx⊕βy,z)=αB(x,z)⊕βB(y,z). We callBalternating ifB(x,x)=0 for allx∈Tm. Otherwise it is called nonalternating. One can see thatTmis anm-dimensional vector space over2. Let {λ0,λ1,…,λm-1} be a basis forTmover2. Then, relative to this basis,Bis uniquely determined by its matrix of sizem×mgiven byB=(bjk)0≤j,k Definition1.3A4-valued quadratic form onTmis a mappingQ[11]:Tm→4with two properties: (1)Q(0)=0; (2)Q(x⊕y)=Q(x)+Q(y)+2B(x,y) whereBis a symmetric bilinear form defined as above.Qis called alternating if its associated bilinear formBis alternating. The rank ofBis defined as rank(B)=m-dim(rad(B)) whererad(B)={x∈F:B(x,y)=0 for ally∈Tm}. The rank ofQis defined as rank(Q)=rank(B). Now letx=(x0,x1,…,xm-1) be the2-valued coordinate vector ofxrelative to the basis {λ0,λ1,…,λm-1} forTmover2. HenceAnd from Definitions 1.2 and 1.3,Q(x)-B(x,x)∈22can be easilydeduced from 2Q(x)=2B(x,x). Therefore, there existsv∈such thatQ(x)=xBx+2vxT. It is known[12]that every4-valued quadratic form can be written uniquely in the following form. Lemma1.4Every4-valued quadratic formQ:Tm→4can be written uniquely as Lemma1.5IfQis an alternating4-valued quadratic form of rankr, then the distribution of {χQ(λ),λ∈Tm} is given in Table 1. Table 1 Value distribution of {χQ(λ),λ∈Tm} for alternating Q Lemma1.6IfQis a nonalternating4-valued quadratic form of rankr, then the distributions of {χQ(λ),λ∈Tm} are given in Tables 2 , 3, respectively. Table 2 Value distribution of {χQ(λ),λ∈Tm} for odd r Table 3 Value distribution of {χQ(λ),λ∈Tm} for even r Throughout this section, letmbe an even integer. In this section, a class of quaternary codes derived from a4-valued quadratic forms is investigated. The Lee weight distributions, Hamming weight distributions and complete weight distributions of the quaternary codes are given, respectively. A class of exponential sum over the Galois ringRis denoted by Leta=c+2c′, wherec,c′∈Tm. Hence ρ1(a,b)=ξ(b,c,c′)= We have the associated bilinear form We need the following lemma later. By Lemma 2.1 and some techniques, we have the following results. ProofIt is sufficient to consider the following cases of the roots ofg(x). Case1Whenc=0,b≠0, it is clear thatg(x) has no solution inTm. In this case, rank(Bb,c(x,y))=m. Case2Whenb=0,c≠0, it is clear thatg(x) has no nonzero solution inTm. In this case, rank(Bb,c(x,y))=m. Then the conclusion follows. From the discussions above, we get the distribution of the exponential sumsρ1(a,b) in the following. Ifm≡0 (mod 4),ρ1(a,b) has the following distribution Ifm≡2 (mod 4),ρ1(a,b) has the following distribution ProofLeta=c+2c′, wherec,c′∈Tm. The proof of this theorem is divided into the following cases. Case1b=c=0. This is a trivial case, one can verify that Case3b=0 andc≠0. In this case,Q(0,c)(x) is nonalternating and rank(Q)=m. Hence by Lemma 1.6, from Theorem 2.4 and Lemma 1.6. Then the conclusion follows. In this subsection, we investigate the Lee weight distributions and Hamming weight distributions of several classes of codes fromρ1(a,b), respectively. For an elementz∈4, define its Lee weight aswhere Re(t) denotes the real part of a complex numbert. For a codewordc=(c1,c2,…,cn), the Lee weight ofcis defined as Now we define a quaternary code as wL(c(a,b))= Then from Theorem 2.5, we can determine the Lee weight distribution ofC1in the following. Table 4 Value distribution of Lee weight with m≡0 (mod 4) Table 5 Value distribution of Lee weight with m≡2 (mod 4) Define the Hamming weight of a codewordc=(c1,c2,…,cn) aswH(c)=#{1≤j≤n:cj≠0}. Now we determine the Hamming weight of the quaternary codeC1. For a codewordc(a,b)∈C, the Hamming weight of it can be expressed as wH(c(a,b))=2m-∣{x∈Tm:c(a,b)=0}∣= Assume thata=c+2c′,c,c′∈Tm. It is easy to verify thatρ1(2a,2b)=2mifc=0 andρ1(2a,2b)=0 otherwise. Thus wH(c(a,b))= From the proof of Theorem 2.5, it is easy to get the distribution of the exponential sumsξ(b,0,c′) as Forc≠0 andm≡0 (mod 4), one can obtain the distribution of the exponential sumsξ(b,c,c′) as Forc≠0 andm≡2 (mod 4), one can obtain the distribution of the exponential sumsξ(b,c,c′) as Therefore, the Hamming weight distribution of the quaternary codes is obtained. Table 6 Value distribution of Hamming weight with m≡0 (mod 4) Table 7 Value distribution of Hamming weight with m≡2 (mod 4) WeightFrequency012m-12m-13·2m-2(2m-1)·(23m2-1+2m-1-2m2)2m-1∓2m2-1(2m2-1)(2m-1±2m2-1)3·2m-2∓2m2-1(2m-2±2m2-1)·(2m-1)(2m2-1)3·2m-2∓23m-24-1(2m-1)·(2m2-1±2m-24) Remark2.8Letφbe the Gray map over4, define wherec(a,b) is defined as above. From Ref.[17],wH(φ(c(a,b)))=wL(c(a,b))=2m-Re(ρ1(a,b)). Thus the Hamming weight distribution ofφ(C1) is the same as the Lee weight distribution ofC1. In this subsection, we investigate the complete weight distribution of the quaternary codeC1. LetNi=Nc(a,b),i=0,1,2,3 denote the number of components ofc(a,b) that are equal toi. Then for a codewordc=(c1,c2,…,cn) over Consider the system of equations One can deduce that N0=2m-wH(c(a,b))= N2=wL(c(a,b))-wH(c(a,b))= Table 8 Complete weight enumerator of C1 with m≡0 (mod 4) N0N1N2N3Frequency2m-102m-102m-12m00012m-1±2m2-102m-1∓2m2-102m2-1 2m-1±2m2-1 2m-22m-22m-22m-22m-2m2 2m-1 2m-2±2m2-12m-22m-2∓2m2-12m-22m-2±2m2-1 2m-1 2m2-1 2m-22m-2±2m2-12m-22m-2∓2m2-12m-22m-1 2m2-1 (each)2m-2±23m4-12m-22m-2∓23m4-12m-22m2-2±2m4-1 2m-1 2m-22m-2±23m4-12m-22m-2∓23m4-12m2-22m-1 (each) Table 9 Complete weight enumerator of C1 with m≡2 (mod 4) ProofWe only give the proof form≡0 (mod 4) since the case form≡2 (mod 4) can be similarly proved. The proof is given in several cases. Case1c=0 andρ1(a,b)=ξ(b,0,c′)=0. In this case,N0=2m-1,N2=2m-2m-1=2m-1,N1=N3=0. From Theorem 2.5, (N0,N1,N2,N3)=(2m-1,0,2m-1,0) occurs 2m-1 times. Then the proof is completed by combining Cases 1—8. Remark2.10Quaternary codes derived from a class of exponential sums a∈R,b∈Tm ρ2(a,b)=ξ2(b,c,c′)= To determine the distribution of the exponential sumρ2(a,b), it is sufficient to consider the rank distribution of the quadratic formQb,c(x)=Trm(cx+2bx2k+1),b,c,x∈Tm. Note thatQb,c(x) is a4-valued quadratic form with associated bilinear form Bb,c(x,y)=trm(c2xy⊕bx2ky⊕bxy2k)= trm(c2k+1x2ky2k)⊕trm(b2kx22ky2k)⊕trm(bxy2k)= trm((c2k+1x2k⊕b2kx22k⊕bx)y2k) Hence it is sufficient to consider the roots of the equation c2k+1x2k⊕b2kx22k⊕bx=0 (1) In the following, we discuss the roots of Eq.(1) in several cases. ProofIfb=0,c≠0, the proof is obvious. To consider the casebc≠0, we need the following lemmas. Lemma3.2[18]Leth(x)=x2k+1⊕x⊕withandD=2gcd(k,m). Thenh(x)=0 has 0, 1, 2 orD+1 solutions inTm. Assume thatnj:=#{∈Tm*∣h(x)=0 hasjroots inTm}. (b,c)→γ Lemma3.3Forb≠0, let g(y)=c2k+1y⊕b2ky1+2k⊕b wherey=x2k-1. Then: Note that gcd(2m-1,2k-1)=2d-1. Then the conclusion follows. DenoteRjasRj={(b,c)∈Tm×Tm{(0,0}: rank(Qb(x))=m-j}. From Lemma 3.1 and Lemma 3.2, we can get the rank distribution ofBb,c(x,y) when (b,c) runs throughTm×Tm{(0,0}. Theorem3.4When (b,c) runs throughTm×Tm{(0,0}, the distribution of rank(Bb,c(x,y)) is Case1b=0,c≠0. From Lemma 3.1, rank(Bb,c(x,y))=m. Case4bc≠0 andg(y)=0 has no solution. In this case, rank(Bb,c(x,y))=m. From Lemma 3.2, This case occurs (2m-1)n0times. Case5bc≠0 andg(y)=0 has exactly one solution. Then from Lemma 3.3, this solution is a (2d-1)th power inTm. This implies that Eq.(1) has 2dsolutions. Hence rank(Bb,c(x,y))=m-d. From Lemma 3.2, this case occurs (2m-1)n1times. Case6bc≠0 andg(y)=0 has two solutions inTm. Then from Lemma 3.3, these two solutions are both (2d-1)th powers or both not (2d-1)th powers inTm. If the former is true, then Eq.(1) would have 2×(2d-1)+1=2d+1-1 roots inTm, which is impossible. Hence both roots are not (2d-1)th powers and Eq.(1) has the unique zero solution. Then rank(Bb,c(x,y))=mand this case occurs (2m-1)n2times. Case7bc≠0 andg(y)=0 has 2d+1 solutions. Then from Lemma 3.3, all of them are (2d-1)th powers inTm. This implies that Eq.(1) has 22dsolutions. Hence rank(Bb,c(x,y))=m-2d. From Lemma 3.2, This case occurs (2m-1)n2d+1times. The proof is completed by combining Cases 1—7. Now we determine the distribution of the exponential sumρ2(a,b). Theorem3.5When (a,b) runs throughR×Tm, the distribution of the exponential sumρ2(a,b) is given as follows. Ifd=gcd(m,k) is odd, where Ifd=gcd(m,k) is even where Case1b=c=0. This is a trivial case, we can obtain that Case3b∈〈ξ2d+1〉,c=0. Note thatBb,c(x,y) is alternating and rank(Bb,c(x,y))=m-2d. Then by Lemma 1.5, when (c,c′) runs through 〈ξ2d+1〉×Tm, we have Secondly, when (b,c) runs throughRdandc′ runs throughTm, we have The proof is finished by combining Cases 1—5. Now we define another class of quaternary codes as C2={c(a,b):a∈R,b∈Tm} wL(c(a,b))=2m-Re(ρ2(a,b)) Then we can determine the Lee Hamming weight distribution ofC2from Theorem 3.5 in the following. Theorem3.6When (a,b) runs throughR×Tm, the Lee weight distributions of the quaternary codeC2are given in Tables 10, 11. Table 10 Lee weight distribution of quaternary code C2 for odd d where Table 11 Lee weight distribution of quaternary code C2 for even d WeightFrequency002mB12m∓2m2B22m∓2m-m-2d2B32m∓2m-m-d2B4 where By using the same method in Section 2, one can easily deduce that Lemma3.7Whenc=0, the distribution ofρ2(a,b) is Whenc≠0 anddis odd, the distribution ofρ2(a,b) is Whenc≠0 anddis even, the distribution ofρ2(a,b) is ProofThe proof is completed by the proof of Theorem 3.5. Theorem3.8When (a,b) runs throughR×Tm, the Hamming weight distributions of the quaternary codeC2are given in Tables 12, 13. Table 12 Hamming weight distribution of quaternary code C2 for odd d Table 13 Hamming weight distribution of quaternary code C2 for even d where ProofThe proof is completed by Lemma 3.7. LetNi,i=0,1,2,3, denote the number of components ofc(a,b) inC2that are equal toi. Note that N0=2m-wH(c(a,b))= N2=wL(c(a,b))-wH(c(a,b))= In the following, we give the distributions of (N0,N1,N2,N3) when (a,b) runs throughR×Tm. Theorem3.9The complete weight enumerator of the quaternary codeC2is given by Table 14 ifdis odd and Table 15 ifdis even when (a,b) runs throughR×Tm. Table 14 Complete weight enumerator of C2 for odd d where Table 15 Complete weight enumerator of C2 for even d where ProofThe proof is completed by Lemma 3.7. Two classes of quaternary codesC1andC2based on two exponential sumsρ1(a,b) andρ2(a,b) over Galois rings are investigated, respectively. The Lee weight distributions, Hamming weight distributions and complete weight distributions of the codes are completely determined. All the distributions in this paper have been verified by computer experiments.


1.2 4-valued quadratic forms




2 Codes Derived from the First 4-valued Quadratic Form
2.1 Distribution of the first exponential sums ρ1(a,b)


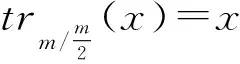
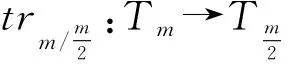









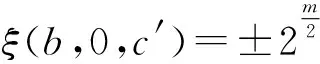
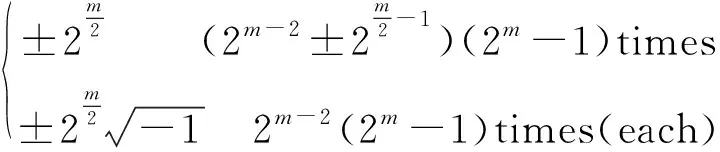
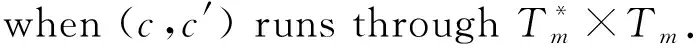



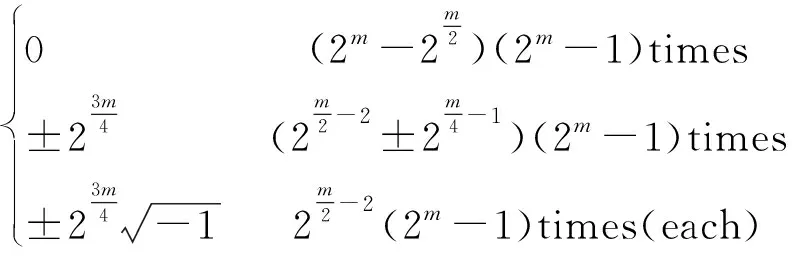


2.2 Lee weight distribution and Hamming weight distribution of C1



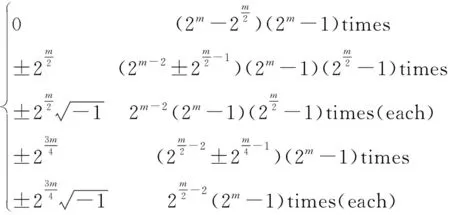




2.3 Complete weight distribution of C1


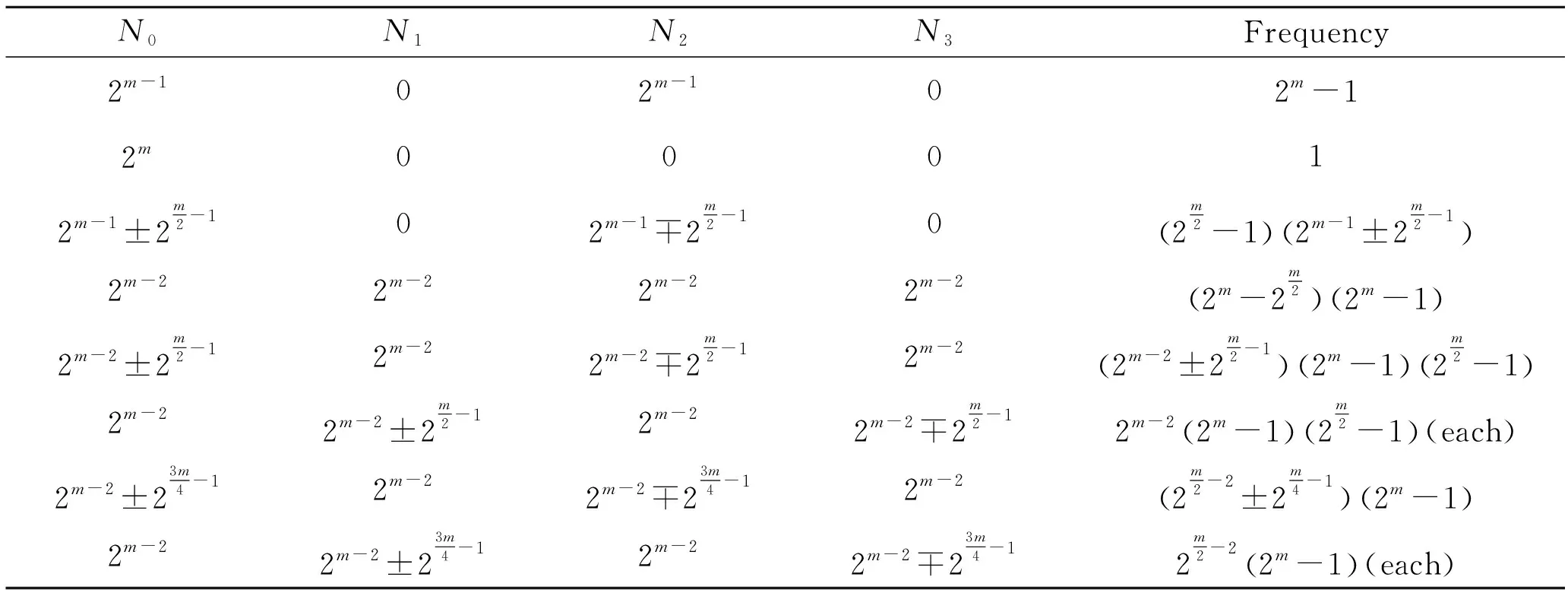

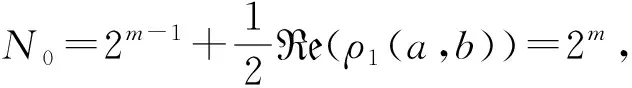






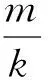
3 Codes Derived from the Second Quadratic Form


3.1 Distribution of exponential sums ρ2(a,b)




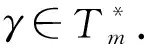



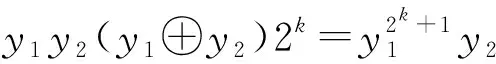
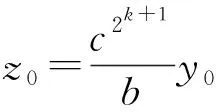

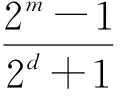










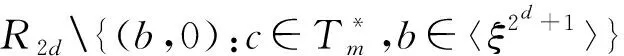
3.2 Lee weight distribution and Hamming weight distribution of C2







3.3 Complete weight distribution of C2


4 Conclusions
杂志排行
Transactions of Nanjing University of Aeronautics and Astronautics的其它文章
- Random Vibration of Steel Catenary Riser Conveying Fluid Under Wave Excitation
- Failure Assessment of Aero-engine Support Structure due to Blade-off
- Nonlinear Control Method for Hypersonic Vehicle Based on Double Power Reaching Law of Sliding Mode
- Dynamic Analysis and Optimization of Pneumatic Wedge-Shaped Launcher for UAV
- Modal and Fatigue Life Analysis on Beam with Multiple Cracks Subjected to Axial Force
- Application of Laser Ultrasonic Technique for Non-contact Detection of Angled Surface Defects
