Dynamic Analysis and Optimization of Pneumatic Wedge-Shaped Launcher for UAV

, , *

1. College of Aerospace Engineering, Nanjing University of Aeronautics and Astronautics,Nanjing 210016, P.R.China;2. Key Laboratory of UAV’s Advanced Technology (Nanjing University of Aeronautics and Astronautics),Ministry of Industry and Information Technology, Nanjing 210016, P.R.China

Abstract: The constitution, structure, working principle and launching process of the wedge-shaped pneumatic launcher of an unmanned aerial vehicle(UAV) are described．By simplifying its physical model, two dynamic models of the UAV launch system are established based on Lagrange equation and MSC.ADAMS, respectively. The curves of the acceleration and the velocity of UAV changing with time are obtained. The simulation results are compared with the experimental results to verify the correctness of the model. Then, the influence of the parameters on the launch is explored. Finally, the system is optimized. The maximum overload and the acceleration fluctuation are reduced.

Key words: unmanned aerial vehicle; pneumatic launching; dynamic simulation; system optimization

0 Introduction

In the application of unmanned aerial vehicle (UAV), the launch phase is usually regarded as one of the most difficult stages[1]. There are many launching modes of UAV, including mother aircraft launching, rocket boosting, vehicle-borne taxi launching, vertical launching, ejection launching, hand-throw launching and so on, among which ejection takeoff mode is the most widely used[2-7]. The pneumatic launch method is an advanced way of kinetic energy ejection developed in 1990s[1]. In this system, the pneumatic energy is used as the power of UAV ejection and the technology has been used for the first time in foreign countries[1-3].

Because of the complexity and difficulty of the technology, only a few countries, such as the United States, Britain and Switzerland, initially mastered it. For example, the “Scan Eagle” and “Shadow” in the United States, the “Phoenix” in Britain and “Patrol” in Switzerland[1].

In China, some universities and institutes, such as Zhengzhou University, China Aerospace Science and Technology Corporation, Aviation Industry Corporation of China, Nanjing University of Aeronautics and Astronautics and Northwest Polytechnic University, have already carried out the research and development of the UAV pneumatic launch system.

Liu Xiaolong deduced the mathematical model of a pneumatic ejection system based on the bond graph method, and through the simulation of different design parameters of the system, the influence of these parameters on the ejection performance of the system was obtained[8]. Li et al. analyzed the system ejection process theory and carried out the research on the present UAV ground ejection system performance by the energy method[9]. Liu put forward the concrete work plan of the launching system of the UAV supplied by the gas storage cylinder, and the mathematical model of the system was established according to the classical physics principle[10]. Lu et al. used the vector method to perform numerical operations on similar systems[11].

Most of the above research work is based on the mathematical modeling and simulation analysis with introduction of hypothesis. There are few studies on the establishment of aerodynamic ejection models by using virtual prototype and the analysis of the differences between different models.

Moreover, there are still some shortcomings in the current UAV pneumatic launch system. For example, it needs enough space and it is difficult to install and operate in narrow space. When small UAV launches, the acceleration fluctuates greatly, and the structure and equipment of UAV may be damaged[12].

In this paper, an UAV wedge-shaped pneumatic launcher is taken as the research object. By simplifying its physical model, two dynamic models of the UAV launch system are established based on Lagrange equation and MSC.ADAMS, respectively. The correctness of the model is verified by comparing the experimental data with the simulation results. Then, the influence of the parameters on emission is discussed. Finally, the system is optimized. It provides a reference for engineering development and subsequent improvement of UAV pneumatic ejection system.

1 Launch Principle

In UAV wedge-shaped pneumatic launcher, the pneumatic energy is used as the power of UAV ejection. Fig.1 shows the schematic diagram of UAV pneumatic launch system. The slider moves to the initial position during launching process. Before starting, the upper slider is restricted by the safety pin. The air pressure cylinder starts to inflate, the cable is preloaded, and the preload lower slider is automatically balanced[11-14]. After reaching the predetermined barometric pressure, the safety pin is removed, the slider is released, and the compressed air stored in the pneumatic cylinder drives the piston to work. Thus it drives the pulley and the UAV to move forward together. When the upper slider reaches its maximum velocity and begins to decelerate, the UAV continues to move forward from the interceptor due to inertia[11-12].

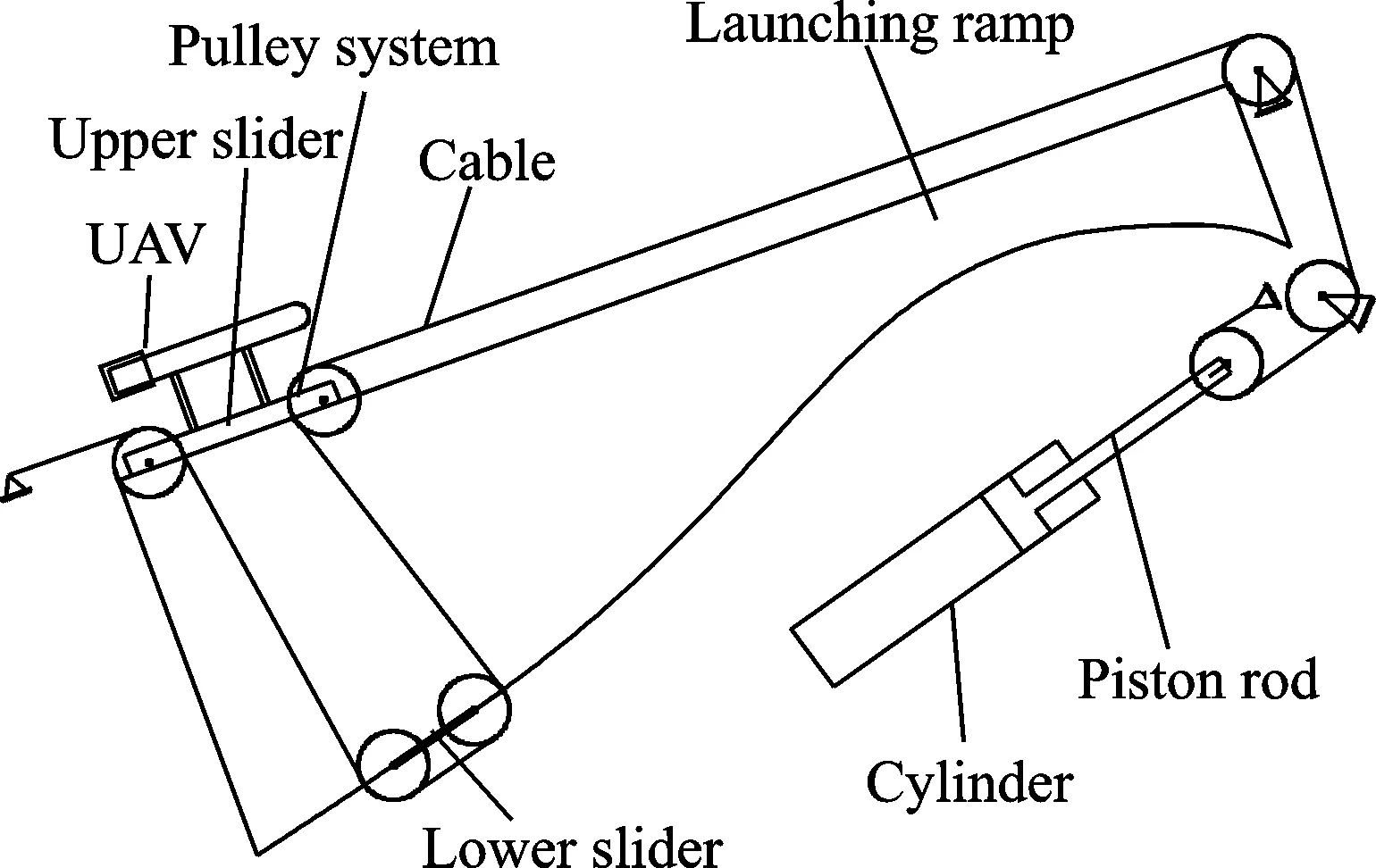
Fig.1 Schematic diagram of UAV pneumatic launch system

2 Model Establishment

2.1 Dynamic model based on Lagrange equation

In the initial stage of the design of pneumatic wedge-shaped launcher, due to the lack of the detailed structural features of the components, a simplified approximate model (Fig.2) is usually used to carry out the dynamic analysis of the system so as to obtain the macro dynamic characteristics of system quickly.

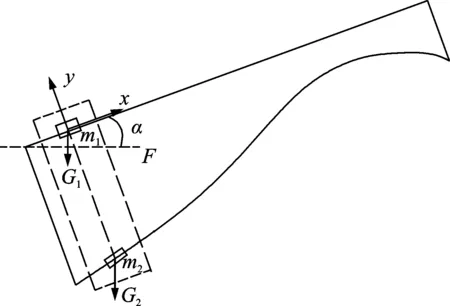
Fig.2 Dynamic analysis model of launch process

In the dynamic model, we assumed that:

(1) The energy used to launch UAV comes from the internal energy of the compressed air stored in the pneumatic actuator. Because the launch process is too fast (about 0.22 s) it cannot carry out significant heat exchange with the outside. This aerodynamic process can be regarded as an adiabatic process.

(2) The upper slider and the lower slider in the UAV are simplified as particles. The mass of the two slides are represented bym1andm2. The mass of the pulley is ignored.

(3) The upper slider and the lower slider are connected through a cable system. It is considered that the displacement of the upper slider is equal to that of the lower slider in thexdirection. The upper slider moves linearly along the upper part of the launcher and the lower slider slides along the wedge of launcher.

(4) The displacement of piston is half of the displacement of the length of the cable. It can be regarded as the displacement of the lower slider according to (3).

The force of pneumatic actuating cylinder is

F=μ(P2-PAtm osphere)S=

(1)

whereΔis the displacement of piston,μis the efficiency of piston actuators,P2is the current cylinder pressure,PAtmosphereis the atmospheric pressure,P1is the inflation pressure,V1is the initial cylinder volume，V2is the current cylinder volume andSis the cross-sectional area of the piston.

The coordinates of the upper and the lower sliders are

R=[x,0],r=[x,f(x)]

(2)

wherexis the displacement of upper slider in thexdirection andf(x) is the function of wedge orbit.

Therefore

(3)

(4)

(m1+m2)gxsinα+m2gf(x)cosα

(5)

whereTis the kinetic energy of the system,Wis the work of force of pneumatic actuating cylinder,αis the launching angle andVis the potential energy of the system.

According to the Lagrange equation, the dynamic differential equation of the system can be given as

(6)

After the dynamic analysis model of UAV aerodynamic launching process is established, the response problem is solved by using the MATLAB platform and the center difference method.

2.2 Multi-body dynamic model based on MSC. ADAMS

The dynamic parameters of UAV in the launching process can be quickly obtained by using an approximate model. The friction between the rope and the pulley, the mass of the rope and the pulley, and the relative displacement of the upper and the lower sliders in thexdirection are ignored in the approximate model.

For the system, the influence of these factors can not be ignored. Therefore, it is necessary to establish a more complete dynamic model. MSC.ADAMS is a simulation software of dynamics of multi-body system. It has been proved essential to build dynamics of multi-body system[15].The multi-body dynamic model of UAV pneumatic launch system is established based on MSC.ADAMS.Fig.3 shows the multi-body dynamic model based on MSC.ADAMS.

Fig.3 Multi-body dynamic model of launch process

The launch system is mainly composed of sliders, launching ramp, pneumatic actuating device and pulley system, as shown in Table 1.

Table 1 Components of launch system

Joints between different parts are listed in Table 2. The upper slider moves linearly along the upper part of the launcher, while the lower slider slides along the wedge of launcher. These motions can be simulated by using module “Translation” and module “Inplane” in MSC.ADAMS.

Table 2 Joints between different parts

The pulley system consists of a flexible rope and seven pulleys, two of which are fixed and the remaining five are movable. Module MSC.ADAMS/Cable packages the roll and the contact algorithms between flexible rope and pulley[15].

Besides, the external force of the system is gravity and pneumatic force. The force of pneumatic actuating cylinder is given by Eq.(1). The launch angle of UAV can be changed by changing the direction of gravity. The system is subjected to friction at each place of relative movement. For example, the friction factor between the slider and the guide rail is 0.005, the kinematic friction factor of the moving pulley block is 0.05, and the friction factor of the pulley bearing is 0.002[16-20].

3 Simulation and Analysis Results

When the UAV reaches the specified position, the sensor SENSOR_1 is set to invalidate the fixed vice between UAV and upper slider to simulate the release process of UAV. Under the initial conditions, the weight of UAV is 20 kg, the initial pressure of the pneumatic actuator is 5.31 × 105Pa and the emission angle is 25°.

Figs.4,5 show the simulation curves of the velocity and the acceleration of UAV varying with time.

Fig.4 Simulation curves of UAV velocity

Fig.5 Simulation curves of UAV acceleration

In the MSC.ADAMS simulation, the launch velocity is 27.1 m·s-1, the maximum overload is 18.08 g, the distance of launching is 3.32 m, and the time of launching is 0.218 s.

In the approximate model simulation, the launch velocity is 27.01 m·s-1, the maximum overload is 18.21 g, the distance of launching is 3.35 m, and the time of launching is 0.22 s.

The difference between the two models for the final and peak values is very small, but there are some differences in the process. Because some assumptions are introduced in the approximate model simulation.

The orbit of the system is wedge-shaped and the wedge angle is a function of length[12]. This makes acceleration approximate a constant value at the initial stage of launch.

The relative displacement of the upper and the lower sliders in thexdirection is ignored in the approximate model simulation. In the MSC.ADAMS model, the factor is taken into account.

Then, the MSC.ADAMS model is used to analyze the launching dynamics, because it is closer to the actual situation.

Fig.6 shows the speed curves of the lower and upper sliders. Their movements are not synchronous. So when the force of the actuator continues to decrease, the acceleration will not decrease rapidly. The advantage of this arrangement is that the acceleration mutation can be reduced and the UAV can be effectively accelerated during launching.

Fig.6 Simulation curves of velocity of upper and lower sliders

Fig.7 shows the simulation of UAV launch every 0.037 s. The distance between the upper and lower sliders decreases with the increase of time.

Fig.7 UAV launch simulation in every 0.037 s

In order to verify the correctness of the model, 40 sets of data are obtained by changing the inflation pressure and mass[11], and are compared with experimental data(Fig.8). The average error is 0.578% and the maximum error is 1.981%. It can fully demonstrate that the dynamic model is correct. On the other hand, adjusting the inflation pressure can meet the requirements of UAV with different weights.

Fig.8 Comparison of simulation results with experimental results of launching velocity

4 Influence of Parameters on Laun-ch Process

The force of the pneumatic actuator has great influence on the acceleration of UAV. It is the source of acceleration for UAV. As the basic structure of the launcher is unchanged, the stroke of the piston rod does not change. The optional design variables are the initial volume of the cylinderV, the piston cross-sectional areaS, the inflation pressureP, and the launching angleα. In addition, a new parameteruis introduced, i.e., the mass ratio of the lower and upper sliders. Without changing the total mass of the system, its changes will change the mass ratio of the two sliders. Its change has little effect on launching velocity. This parameter mainly determines the motion relationship between lower and upper sliders and has an effect on the acceleration curve. Table 3 shows the design variables.

Before optimization, the relationship between variables and the overload of UAV should

Table 3 Design variables

be studied. Fig.9 shows the influence law of maximum overload, piston area and inflation pressure by a three-dimensional surface.P0is the inflation pressure,Sis the piston area, and “Overload” means the maximum overload during launching. The overload increases with the inflation pressure and the piston area.

Fig.9 Overload for different inflation pressures and different piston areas

Fig.10 gives the acceleration curves changing with time under differentu. The increase ofureduces the peak acceleration of the end. So its change may make the maximum acceleration larger or smaller. Based on practical considerations, its value does not exceed 0.6.

Fig.10 shows that increasingufrom 0.2 to 0.3 reducesamaxby 6.7%, increasingufrom 0.3 to 0.4 reducesamaxby 8.05 %, increasingufrom 0.4 to 0.5 reducesamaxby 4.05 %, and increasingufrom 0.5 to 0.6 reducesamaxby 1.13 %.

Fig.10 Acceleration-time curves for different u

By reducing the launch overload, the service life of the launch system and UAV can be prolonged. In order to make the emission overload as small as possible, the parameters of the pneumatic device can be optimized while keeping the velocity of launching constant.

The launch angleαhas little effect on the process. The optimization design variables can be given as

X=[V,S,P0,u]

(7)

The goal of optimization is to minimize the maximum acceleration in the operation of the prototype model. The objective function can be expressed as

f(X)=min(Maximum of Modle1.ACC)

(8)

The design constraint is expressed as a function of the small range of the launching velocity

g1(X)=V-27.2

g2(X)=27-V

(9)

As shown in Fig.11, the maximum acceleration is reduced, the acceleration fluctuation is decreased obviously, and the launching velocity is basically unchanged, which achieve the optimization design goal. Table 4 shows the original and optimized results of design variables. Table 5 shows the original and optimized results.

Fig.11 Original and optimized curves of acceleration

VariableV/LP0/MPauS/m2Original630.5310.5726.7e-2Optimized730.5200.5846.3e-2

Table 5 Optimized result

5 Conclusions

An UAV with wedge-shaped pneumatic launcher is taken as the research object. Based on Lagrange equation and MSC.ADAMS, the dynamic models of the UAV pneumatic launch system are established according to the motion law of each part. Simulation curves of the acceleration and the velocity of UAV are obtained, and the performance characteristics of the pneumatic launch system are studied.

The simulation results are in good agreement with the experimental results, which proves the correctness of the model. The simulation results show that the UAV pneumatic launch system can output acceleration close to the ideal constant, and can quickly reduce acceleration. The initial volume of cylinder, piston cross-sectional area and inflation pressure are key parameters affecting the launching acceleration process and the launching velocity. By changing these parameters, the requirements for the launching velocity of different weight aircraft can be meet. It provides a reliable basis for the design and experiment of the UAV pneumatic launch system. Through system optimization, the maximum overload of UAV is reduced, and the fluctuation of acceleration phase is reduced. It can reduce the impact of launch phase on UAVs and airborne equipment.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (No.11602105), and the Natural Science Foundation of Jiangsu Province (No.BK20160782).