Modal and Fatigue Life Analysis on Beam with Multiple Cracks Subjected to Axial Force

, ,

1.School of Naval Architecture and Ocean Engineering, Jiangsu University of Science and Technology,Zhenjiang 212003， P.R. China; 2.State Key Laboratory of Mechanics and Control for Mechanical Structures, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, P.R. China

Abstract: Based on the transfer matrix method and Forman equation, a new method is proposed to conduct the modal and fatigue life analysis of a beam with multiple transverse cracks. In the modal analysis, the damping loss factor is introduced by the complex elastic modulus, bending springs without mass are used to replace the transverse cracks, and the characteristic transfer matrix of the whole cracked beam can be derived. In the fatigue life analysis, considering the interaction of the beam vibration and fatigue cracks growth, the fatigue life of the cracked beam is predicted by the timing analysis method. Numerical calculation shows that cracks have a significant influence on the modal and fatigue life of the beam.

Key words: beam; cracks; axial force; natural frequency; fatigue life

0 Introduction

Beam structures have been widely applied in engineering practice, including shipbuilding industry, machinery manufacturing, construction industry, aerospace industry, and so on. During the manufacturing and assembling procedures, beams would suffer different degrees of structural damages. The most common form of structural damage is the crack, and the existence of cracks will change the dynamic characteristics of the beam, such as natural frequencies and mode shapes. These changes depend on the number, positions and depths of cracks. Many studies have been conducted in this area, and several models have been proposed to calculate the natural frequency of the cracked beam, such as the finite element method[1], the transfer matrix method[2], the dynamic stiffness method[3], the boundary element method[4], etc.

For the beam subjected to the axial force, many researchers had investigated the free vibration of these beams. In Ref.[5], the modal analysis was conducted of a Rayleigh cantilever beam with axial load and tip mass, and also the simple fundamental frequency formula was derived. In Ref.[6], the exact closed-form solution was used to calculate the natural frequencies, the corresponding natural modes and buckling load of the beam-column. Considering the bending-torsion coupling effect, the dynamic stiffness method was used to derive the dynamic matrix of a cracked beam, and the effect of the crack on the modal characteristics of the beam was investigated in Ref.[7]. The boundary conditions and recursive formulas were used in Refs.[8-9] to reduce the difficulty to find the roots of the second-order determinant. Particularly, a model of massless rotational spring was adopted to obtain the local flexibility caused by cracks, and the free vibration of a non-uniform beam with an arbitrary numbers of cracks and the concentrated mass was analyzed in Ref.[8]. In Ref.[10], the finite element method was used to conduct the dynamic analysis by taking into account the effect of axial force. However, these researches mentioned above only investigated the free vibration, and did not conduct the fatigue life analysis of these cracked beams, which would cause the vibration fatigue failure of the structures.

Around 1960, Boeing found that the stress intensity factor played a key role in the fatigue crack extension firstly. In 1963, Paris and Erdogan[11]contacted the crack growth data and the stress intensity factor amplitude, and established the theory of the fatigue fracture. With the development of fracture mechanics, several methods[12-14]have been proposed to predict the fatigue life of cracked structures. However, these researches used the static method to calculate the stress, with the assuming that the stress had nothing to do with the external excitation frequency and damping. Refs.[15-16] considered the effect of excitation frequency on the fatigue life of the cracked structure. Based on the S-N curve, Ref.[17] proposed a fatigue assessment method for composite wind turbine blade by the finite element method. Ref.[18] used the finite element method to investigate the stress distribution of the cantilever aluminum alloy beam. Ref.[19] studied the effect of axial excitation frequencies on the fatigue crack growth life of polymer materials in resonance conditions. But these researches neglected the influence of the number of cracks and the axial force.

The objective of this paper is to propose a theoretical method to calculate the natural frequencies and predict the fatigue life of a beam with multiple cracks. Based on the transfer matrix method, a transfer matrix with the characteristics of cracks and the axial force is derived, and natural frequencies of the beam are obtained by the implementation of the boundary conditions. Considering the interaction of cracked beam vibration and cracks growth, the fatigue life of the beam is predicted by using the timing analysis method and Forman equation, and the accuracy of estimating the fatigue life is further improved.

1 Model

The model of beam with multiple cracks is shown in Fig.1. As shown in Fig.1, an isotropic and rectangular cross-section beam withntransverse cracks is given, and each transverse crack is modeled as the bending spring without mass. The depths of cracks area1,a2,…,an, and the positions of cracks areL1,L2,…,Ln, respectively.

Fig.1 Model of beam with multiple cracks

According to the theory of Dimarogonas and Paipeties[20], the local flexibility caused by each crack can be written as follows

(1)

wherei=1,2,…,n;αiis the local flexibility caused by crack No.i, andαican also be considered as the flexibility of the bending spring No.i;E*is the complex elastic modulus,E*=E(1+iγ), andEis the storage modulus;γis the material damping loss factor;Iis the moment of inertia of the cross section;ri=ai/his the relative depth of crack No.i;his the height of the cross-section of the beam;f(ri) is the local flexibility function of the crack No.i, and can be obtained through the strain energy density function

(2)

Considering each transverse crack as a breakpoint of the beam, the whole beam is divided inton+1 intact sections byncracks. Then+1 intact beams are connected bynbending springs without mass, and each intact beam has the lengthli(i=1,2,…,n+1). The vibration differential equation of Euler-Bernoulli beam can be expressed as

(3)

wherexi∈[0,li];Ais the area of the cross section of the beam;ρis the density of the beam structure material; andSis the axial force applied on the cross-section of the beam.

The solution of Eq.(3) can be assumed as

wi(xi,t)=Ui(xi)qi(t)

(4)

Substituting Eq.(4) into Eq.(3) yields two ordinary differential equations

(5)

(6)

(7)

2 Transfer Matrix Method

According to mechanics of materials, the angle of deflectionθ, the bending momentMand the shearing forceQcan be obtained as follows

(8)

At the left end of each intact beam, the above formulas are used, and the deflection, the angle of deflection, the bending moment and the shearing force can be obtained as

(9)

Transforming these equations into the form of the matrix

(10)

where

(11)

Similarly, at the right end of each intact beam, the above formulas are used and the deflection, the angle of deflection, the bending moment and the shearing force can be obtained

(12)

Transforming these equations into the form of matrix

(13)

where

Si=

(14)

Substituting Eq.(10) into Eq.(13) yields the equation of each intact beam

(15)

At the location of the crack No.i, the crack is replaced by the bending spring without mass, the angle of deflection, the bending moment and the shearing force between the left and right sides of the crack can be expressed as follows[5]

(16)

Then the transfer matrix of the crack No.ican be obtained

(17)

(18)

whereTiis the transfer matrix of the crack No.i.

So, for the whole beam withntransverse cracks, the transfer relationship between the state vectors of the right end and left end can be given by

(19)

(20)

Take the cantilever beam for example, the deflection and angle of deflection of the clamped end are equal to zero, and the bending moment and shearing force of the free end are equal to zero

(21)

detHCF=0

(22)

Use the storage modulus to replace the complex elastic modulus when solving the natural frequency of the cracked beam. From Eq.(22), each order natural frequency of the whole beam can be calculated and the corresponding inherent vibration mode can be obtained by Eq.(7).

3 Analysis on Fatigue Life

3.1 Dynamic stress analysis

Assume that the cracked beam is a cantilever beam, and the free end of the beam is subjected to a harmonic excitation in a vertical directionF0eiωt. The corresponding bounding condition can be written as

U1(0)=0,θ1(0)=0

Mn+1(ln+1)=0,Qn+1(ln+1)=F0eiωt

(23)

Substituting Eq.(23) into Eq.(19) yields the deflectionU1(0), the angle of deflectionθ1(0), the bending momentM1(0) and the shearing forceQ1(0). Substituting these vectors into Eq.(8) yields the coefficient of the vibration mode function of the beam No.1(c11,c12,c13,c14). By analogy, the vibration mode function of each section of the beam can be obtained.

As shown in Fig.1, transverse cracks on the beam belong to the most common form of engineering cracks (the open crack), which plays a significant role on the structural damage. So this paper takes the open cracks as the research key, and neglects the influence of the shear stress. The normal stress on the cross-section of the beam is superposed by the normal stresses generated by the axial forceSand the longitudinal forceF0.

The transverse cracks are the unilateral cracks, and the axial force at the free end can be transformed into the axial forceSand the bending momentMs=Sai/2 at the cross-section of the crack.

The normal stress at the crack tip on the cross-section caused by the axial force can be expressed as

(24)

According to Hooke’s law, the normal stress on the cross section caused by the bending moment can be written as

(25)

For the intact beam No.i, the normal stress response at the surface of the beam can be written as

(26)

wherezis the distance from the surface to the middle surface of the beam.

(27)

The amplitude of the dynamic stress at the crack tip can be obtained

σimax=σi,S+σi,Ms+σi,F0

(28)

3.2 Dynamic stress intensity factor

The dynamic stress intensity factor is the physical quantity to characterize the crack tip stress field distribution, and the dynamic stress intensity factor at the crack tip can be expressed as

(29)

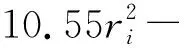
Under the harmonic excitation, the amplitude of the dynamic stress intensity factor at each crack tip can be expressed as

(30)

3.3 Fatigue crack growth life

Due to the axial force, the stress ratio will change during the vibration of the cracked beam. Considering the influence of the stress ratio, the Forman equation is used to simulate the propagation of the fatigue crack[22]

(31)

whereC,nare the crack propagation test constant; da/dNis the fatigue crack growth rate;Ris the stress ratio; andKICis the fracture toughness.

Substituting Eq.(30) into Eq.(31) yields the fatigue crack growth rate of each crack

(32)

Considering the interaction of cracked beam vibration and cracks growth, this paper adopts the timing analysis method, in which the vibration analysis and the fatigue life analysis of the cracked beam are conducted at the same time.

Using Eq.(30), the fatigue crack growth increment of each crack can be calculated when the cracked beam has gone through ΔNjperiodic vibration

(33)

Eq.(33) can be transformed as follows

(34)

where Δaijis the fatigue crack growth increment of the crack No.iwhen the cracked beam has gone through thejth periodic vibration.

In the harmonic excitation with constant amplitude, the depth of the crack can be given by the method of superposition

(35)

whereai0is the initial depth of the crack No.i;kis the vibration cycles;aikis the depth of the crack No.iafter the cracked beam has gone throughkperiodic vibration.

3.4 Fatigue crack failure criterion

To determine the failure of the cracked beam, this paper adopts the following criterions:

Criterion1If any crack extends to the middle surface of the cracked beam, it is considered that the cracked beam has been destroyed.

ai≥ac

(36)

whereacis the critical crack length and in this paper,ac=h/2.

Criterion2If the stress intensity factor at any crack tip is greater than the material fracture toughness, it is considered that the cracked beam has been destroyed.

Kmax≥Kc

(37)

whereKmaxis the maximum stress intensity factor; andKcis the material fracture toughness.

Criterion3If the nominal stress at the location of the crack is greater than the material ultimate strength, it is considered that the cracked beam has been destroyed.

σmax≥σb

(38)

whereσmaxis the maximum dynamic stress at the location of the crack, andσbis the material ultimate strength.

4 Results

According to the coordinate system of Fig.1, the geometric parameters of the beam are:L=0.3 m,h=0.02 m,b=0.02 m. The structural material is the alloy steel 30CrNi4MoA[23], and its material parameters are:E=210 GPa,γ=0.05,v=0.33,ρ=7 860 kg/m3,σb=990 MPa,n=1.272 47,C=7.76×10-8,KIC=177.7 MPa·m0.5.

4.1 Influence of axial force on natural frequency

Taking the cantilever beam for example, assume that the axial forceS∈[0,500 N], and the first order natural frequency of the cracked cantilever beam can be calculated by the analytical method proposed in this paper. Assuming that the axial force has the following values:S=0, 100, 200, 300, 400 and 500 N, and the first order natural frequency of the cracked cantilever beam can be obtained by the finite element method. Consider the following four different cases:

(1) There is no transverse crack on the cantilever beam.

(2) There is only one transverse crack on the cantilever beam, and the geometric parameters are:L1/L=0.1,a1/h=0.1.

(3) There are two transverse cracks on the cantilever beam, and the geometric parameters of cracks are:L1/L=0.1,a1/h=0.1;L2/L=0.2,a2/h=0.1.

(4) There are three transverse cracks on the cantilever beam, and the geometric parameters of cracks are:L1/L=0.1,a1/h=0.1;L2/L=0.2,a2/h=0.1;L3/L=0.3,a3/h=0.1.

The first order natural frequencies calculated by the analytical method and the finite element method are shown in Fig.2.

Fig.2 Variation of natural frequencies of beam with different axial force and crack parameters

As shown in Fig.2, the first order natural frequencies of the cracked beam obtained by two methods are really close, and the biggest error is about 0.367%. So it can be concluded that the analytical method proposed to calculate the natural frequency of the cracked beam subjected to the axial force is correct and feasible. The first order natural frequency gradually increases as the axial force increases. The first order natural frequency gradually decreases as the number of cracks increases.

4.2 Influence on position of cracks

The free end of the beam is subjected to a harmonic excitation in a vertical direction (F0eiωt), andF0=100 N. Assume that the axial force is the real constant (S=200 N), and there are only two transverse cracks on the cantilever beam. Consider that the geometric parameters of cracks are:L1/L=0,a1/h=0.1;L2/L∈(0,1),a2/h=0.1. Assume that the cracked beam keeps in the resonance state, then the variation of fatigue life and initial natural frequencies of the beam at the resonance condition with different positions of the second crack is shown in Fig.3.

Fig.3 Variation of fatigue life and initial natural frequencies of beam with different positions of the second crack

As shown in Fig.3, the fatigue life and the natural frequency gradually increase as the relative position of the second crack increases, and the increasing rate gradually decreases. At the resonance condition, the variation of the fatigue life of the cracked beam is the same as the initial natural frequency, and the influence of the second crack on the natural frequency and the fatigue life of the cracked beam gradually decreases as the second crack is away from the fixed end.

4.3 Influence of damping on fatigue life

The free end of the beam is subjected to a harmonic excitation in vertical direction (F0eiωt), andF0=50 N. The axial force is a constant, andS=0 N. If the damping loss factor has different valuesγ=0.005, 0.01, 0.05, 0.1, there is only one crack on the beam and the geometric parameters of the crack are:L1/L=0.1,a1/h=0.1. Assume that the cracked beam keeps in the resonance state, and the variation of the fatigue life of the beam at the resonance condition with different damping loss factors is shown in Fig.4.

As shown in Fig.4, whenγ=0.005, 0.01, two fatigue life curves almost coincide because the effect of small damping on the fatigue crack growth rate is not obvious, but big damping has large effect on the fatigue life of the cracked beam. The fatigue life of the cracked beam gradually increases as the damping loss factor increases.

Fig.4 Fatigue life of beam with different material damping loss factors

4.4 Influence of axial force on fatigue life

The free end of the beam is subjected to a harmonic excitation in vertical direction (F0eiωt), andF0=50 N. If the axial force has different valuesS=0, 100,…，1 400 N andγ=0.05, consider three different cases:

(1) There is only one transverse crack on the cantilever beam, and the geometric parameters are:L1/L=0.1,a1/h=0.1.

(2) There are two transverse cracks on the cantilever beam, and the geometric parameters of the cracks are:L1/L=0.1,a1/h=0.1;L2/L=0.2,a2/h=0.1.

(3) There are three transverse cracks on the cantilever beam, and the geometric parameters of the cracks are:L1/L=0.1,a1/h=0.1;L2/L=0.2,a2/h=0.1;L3/L=0.3,a3/h=0.1.

Assume that the cracked beam keeps in the resonance state, and the fatigue lives of the cracked beam in these three cases are shown in Fig.5.

Fig.5 Fatigue lives of beam with different numbers of cracks and axial forces

As shown in Fig.5, when the axial forceS∈[0,200 N], the fatigue life of the cracked beam gradually decreases as the axial force increases, because the increasing rate of the normal stress caused by the axial force is larger than the decreasing rate of the normal stress caused by the bending moment. When the axial forceS≥200 N, the fatigue life of the cracked beam gradually increases as the axial force increase, because the increasing rate of the normal stress caused by the axial force is smaller than the decreasing rate of the normal stress caused by the bending moment. The fatigue life of the cracked beam with the same axial force gradually decreases as the number of cracks increases.

5 Conclusions

The bending springs without mass are used to replace the transverse cracks, and the influence of the axial force and cracks parameters on the modal and fatigue life of the cracked beam is investigated based on the transfer matrix method and Forman equation.

The suggested method can investigate the free vibration of the beam subjected to axial force with any arbitrary number of cracks effectively, and can also predict the fatigue life of the cracked beam more accurately. Compared with the finite element method, the theoretical method proposed to conduct the modal analysis can be proved in this paper, and it can also be applied to the simply supported beam, double clamped beams and other cracked beam structures.

Acknowledgement

This work was supported by a project funded by the Priority Academic Program Development of Jiangsu Higher Education Institutions (PAPD).