新课标下数学概念课的教学探究
——以实数概念课为例
2018-11-21赵晓利
赵晓利
(安阳市教育教研信息中心,河南 安阳 455000)
数学概念是构建数学理论大厦的基石,是导出数学定理和数学法则的逻辑基础,是提高解题能力的前提,是数学学科的灵魂和精髓,因此数学概念的学习在数学教学中起着基础的作用。但在实际数学教学过程中,受应试教育的影响,概念的教与学往往易被不少教师和学生忽视,时常发生不用数学概念形成规律去组织教学的现象,其中比较突出的问题就是只注重数学概念所含知识点的教学以及在解题过程中的应用,而不太注重对数学概念形成和内涵的真正了解,特别是忽视数学概念形成过程中所包括的思维方法的教学,即往往注重概念习题课(应用)教学,而不重视对概念新授课的教学研究。对数学概念本质的理解和深化,是数学概念应用的基础,对整个数学知识体系的建立起着重要的作用,因此我们必须要重视概念新授课的教学。作者认为对数学基本概念应该“在理解的基础上记忆,在应用的过程中加深理解”。下面我们将用义务教育课程标准实验教科书八年级上册实数概念课这一案例来具体探讨数学概念课的教学。
1 教材分析
2 学情及教法分析
3 教学目标
(1)知识与技能: 了解无理数,实数的概念,知道实数与数轴上的点一一对应。初步会用数轴上的点来表示实数,会对实数的分类进行初步的辨认;(2)数学思考: 让学生经历数的扩充和实数分类的思维过程;(3) 问题解决: 学生了解实数的概念,知道实数的分类,会区分有理数和无理数;(4)情感态度: 通过自主学习,让学生经历无理数的产生过程,通过合作探究初步理解实数与数轴上的点一一对应,并向学生渗透数形结合和分类讨论的数学思想。
4 教学流程安排
4.1 情景引入,感悟概念
师:七年级上册我们已经学过有理数,有理数都包括哪些数呢?
生:正整数,负整数,正分数,负分数……。
师:除了这些数我们还学过哪些数?
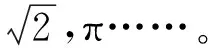
师:这些数叫什么数呢?我们学过的所有数又叫什么数呢?这就是我们今天要学习的实数。
4.2 探究思考,形成概念
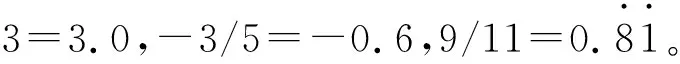
共同得到结论:有限小数和无限循环小数叫有理数,反过来,任何有限小数和无限循环小数也都是有理数。
师:把π写成小数形式,你能发现什么?与上面的数化成小数有什么不同?
学生自主探究,同桌交流,代表发言。
共同得到结论:π是无限不循环小数,叫无理数。
师:你还能举出些无理数吗?无理数具有什么特征?
学生分组讨论,合作探究,代表发言。
师生:有理数和无理数统称为实数。
4.3 剖析理解,巩固概念
师:类比有理数的分类,我们可以把实数如何分类呢?
学生进行小组合作探究,代表发言。在学生发言中要提示学生按照标准,不重不漏。
教师展示学生讨论结果,并给出按定义和性质分类的标准答案。
4.4 拓展创新,延伸概念
师:下面请同学们把1/2,0,-3这些数在数轴上表示出来。
学生动手,自主探究。教师展示结果:

师:每个有理数都可以用数轴上的点来表示,无理数能否用数轴上的点来表示呢?你能在数轴上找到表示π的点吗?
学生利用π的由来,进行小组合作探究,探讨π所代表的具体长度。
探究:如图下图所示,直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上的一点由原点到达点O′,点O′的坐标是多少?
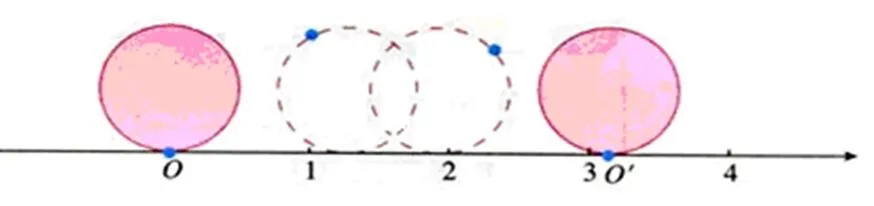
从图中可以看出这个圆的周长是______,OO′的长是___ 点O′的坐标_______ 。
教师利用课件动画演示上圆的周长表示在数轴上,得到结论:无理数π可以用数轴上的点表示出来。
师生:事实上,每一个无理数都可以用数轴上的点表示出来,也就是数轴上的点有有理数有无理数。每一个实数都可以用数轴上的点表示;反过来,数轴上的每一个点都表示一个实数。实数与数轴上的一一对应。
5 课后总结
新课标下的这节实数概念课从四个环节进行探究性学习:情景引入,感悟概念;探究思考,形成概念;剖析理解,巩固概念;拓展创新,延伸概念。教学中重点突出,难点达到突破,完成教学目标,收到良好的教学效果。
在数学教学中,加强概念新授课的教学,使学生正确理解数学概念是掌握数学基础知识的前提,是学好定理、公式、法则和数学思想的基础。良好的数学概念课教学,能使学生透彻、牢固地掌握数学概念,提高数学思维能力。教师应该充分认识到数学概念教学的重要性,在加强数学基础知识的教学的同时培养学生运用数学知识解决实际问题的能力,发展学生逻辑思维和空间想象能力。
