关于多元函数极限求法的探究
2018-11-21杜玉平
杜玉平
(山西朔州师范高等专科学校 数学与计算机系,山西 朔州 036000)
高等数学中多元函数的极限是一个重要概念,很多高等数学中的其它概念都与之密切相关,比如多元函数连续、微分、积分等内容[1]。因此,想学好高等数学,掌握好多元函数的极限是十分重要的。而多元函数的极限的关键内容就是其性质和求法。在本文中,结合多元函数极限的一些性质[2],通过实例总结了几种多元函数极限的计算方法。
多元函数极限的四则运算性、无穷小量性、两边夹定理、罗比达法则以及连续性等都是计算函数极限的重要方法,所以要很好地掌握,并会灵活运用他们。
1 利用函数的重要极限
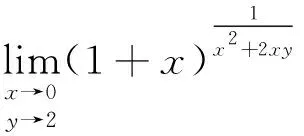
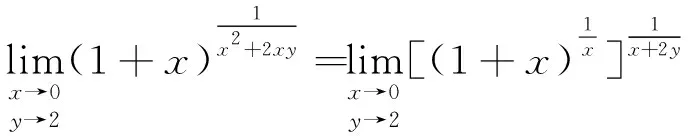
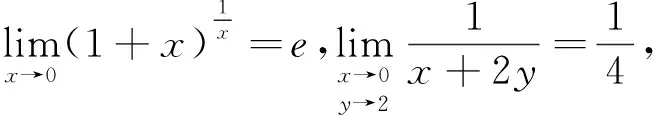
2 利用性质:无穷小量×有界变量=无穷小量
定理1 (无穷小量性):无穷小量×有界变量=无穷小量

当使用此性质求极限时,我们必须首先分析函数是否是无穷小量和有界量的乘积,如果是才可用其计算,不能盲目使用。
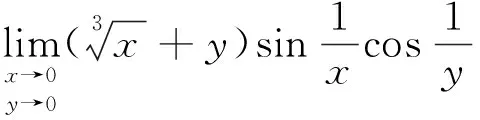
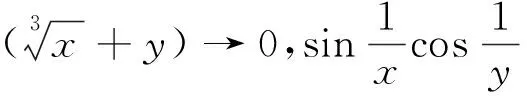
3 利用两边夹定理
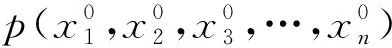
利用该性质计算时,需要找到满足所求极限函数f(x1,x2,…,xn)的不等式关系g(x1,x2,x3,…,xn)≤f(x1,x2,x3,…,xn)≤t(x1,x2,x3,…,xn),有时候,我们需要把所求极限函数f(x1,x2,…,xn)给它放大或缩小,找到g(x1,x2,x3,…,xn)和t(x1,x2,x3,…,xn),然后求出满足两边夹定理的不等式关系,并用两边夹定理求解。
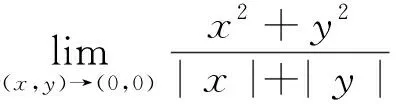
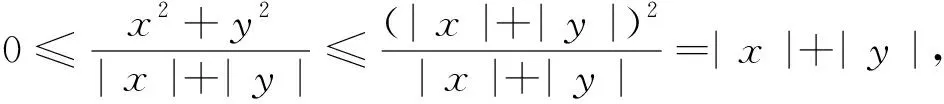
4 利用罗比达法则计算
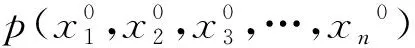
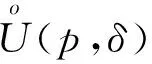
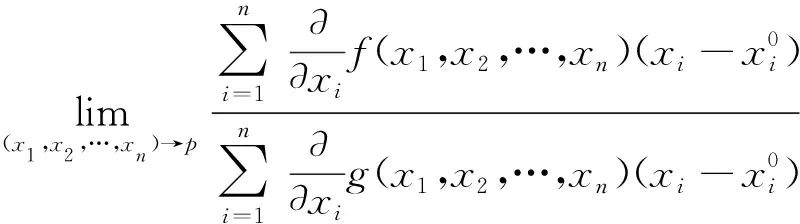
=A(或∞)
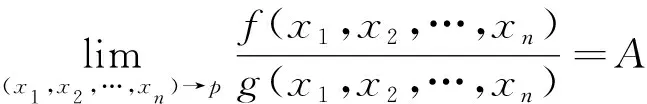
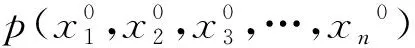
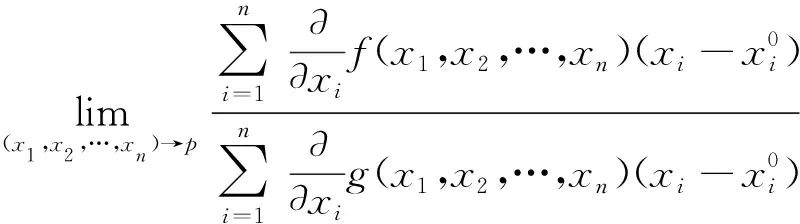
=A(或∞)
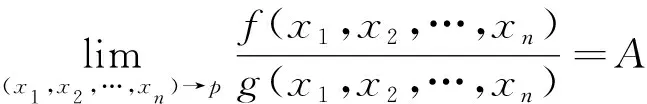
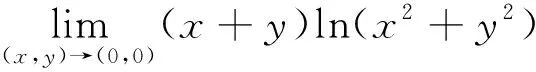
解 由定理3得:
5 通过变量代换求极限
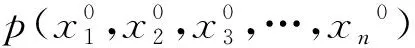
一元函数的极限求法有好多,利用等量代换可以把一些多元函数的极限转化为一元函数,进而可用一元函数的极限求法求。
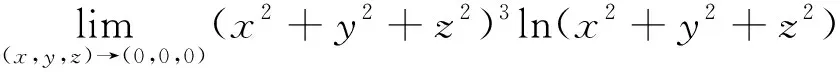
解 由定理4得:
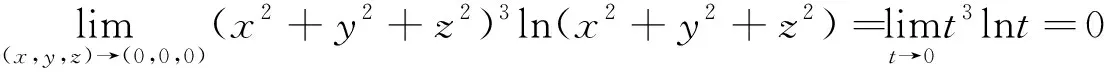
6 利用初等函数的连续性
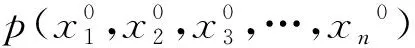
【注】 由连续的定义可得该结论。通常,在定义域上,多元初等函数是连续的[5]。
我们在高等数学中研究的大多数多变量函数都是初等函数,并且所有多元初等函数在它们定义域上都是连续的。所以有些多元函数的极限可直接利用多元函数连续定义计算,但计算前,一定要判断函数在所求极限的点是否连续,连续才可用其计算。
例6
解 因为
在定义域连续,(0,0,1)在定义域内,所以
=f(0,0,1)=sin1
7 利用转化成指数的方法
要求的极限函数是幂指函数形式f(x1,x2,x3,…,xn)φ(x1,x2,x3,…,xn),通常采用先把函数转化成指数函数后再求极限,幂指函数化为指数函数:
f(x1,x2,x3,…,xn)φ(x1,x2,x3,…,xn)
=eφ(x1,x2,…,xn)lnf(x1,x2,…,xn)。
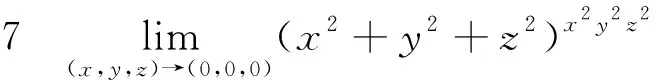
解 令f(x,y,z)=(x2+y2+z2)x2y2z2=eln(x2+y2+z2)x2y2z2=ex2y2z2ln(x2+y2+z2),而
x2y2z2ln(x2+y2+z2)
所以
=e0=1。
以上是我们结合多元函数极限的一些性质总结了多元函数f(x1,x2,…,xn)极限的几种计算方法,并结合例题对一些性质和解题方法进行了演算和应用。其实多元函数极限的性质和极限计算方法远不止文中所提的这些,还有待我们不断地去研究和完善。
