点云模型特征面分割与识别方法
2018-11-20袁小翠陈华伟
袁小翠,陈华伟
(1.南昌工程学院 江西省精密驱动与控制重点实验室,南昌 330099; 2.贵州师范大学 机电工程学院,贵阳 550025)
0 概述
在逆向工程应用领域,重建的产品外形比较复杂,由多个连续性或种类不同的特征面按照不同的拼接条件构成,如平面、球面、圆柱面和过渡面。对一些复杂曲面,单纯用一种几何模型去拟合得到的拟合曲面准确性差。在对产品的CAD模型重构之前,一般需要将复杂产品的不连续曲面分割成若干个连续曲面,准确识别每个特征曲面的类型后对不同的曲面分别建模,再将这些曲面拼接以构成完整产品。因此,点云模型特征面分割与识别是曲面准确重建的基础。
散乱点云数据分割主要分为基于三角网格模型和基于散乱点云的数据分割方法[1]。基于三角网格模型分割需要对点云进行曲面重建,然而三维点云曲面重建比较耗时,基于点云的数据分割直接对点云模型进行分割,不需要对曲面进行重建,吸引了越来越多的关注。目前,点云数据分割方法可以归纳为3类,分别是基于边界检测、区域增长和聚类的分割算法[2]。基于边界的分割方法主要通过查找点云模型的不同特征面的过渡边界,对边界线拟合从而将一个复杂曲面划分为多个独立的特征面。文献[3]通过提取点云的几何属性值如法向量和曲率等,将点云的法向量映射到高斯球上,不同连续曲面映射到高斯球上的不同区域,同一片连续曲面映射到高斯球上的同一片区域,再根据边界线的区域分割出如二次曲面、拉伸面和直纹面等特征曲面。基于区域生长的模型分割方法的关键在于种子点的选取和生长规则,通过选定种子点,按照一定的生长规则将满足条件点合并在同一区域中。比如:文献[4]采用区域生成算法对LiDAR点云提取建筑物和植被区域,且取得了满意的结果;文献[5]计算每个采样点的法向量,然后根据点云法向量检测出点云模型中平滑区域,利用区域增长法对点云模型进行分割,与基于区域增长的分割算法相比,聚类方法并不需要初始化种子点和设计生长规则,其关键在于确定点云聚类模式;文献[6]采用K-means聚类法对三维点云模型进行分割,但是该方法的缺点在于聚类中心初始化和K值的确定;文献[7]基于3D活动轮廓模型对点云进行分割,通过提取模型的轮廓,将点云数据模型分割成若个干不同的区域;文献[8]利用谱聚类算法对点云数据分块,根据归一化的非对称Laplacian矩阵构造谱聚类空间,通过特征精简,在更低维的空间中进行点云分割。
目前虽然已有不少点云数据分割的方法,但许多点云处理专业软件,如Geomagic和Imageware,都不能实现完全点云自动分割,只能通过手动和算法相结合的方法实现数据分块,模型分割和特征面识别速度和准确性有待改进。为此,本文在准确估算点云法矢的基础上采用高次曲面估算点云曲率,并根据平均曲率和高斯曲率将点云划分为8种类型,通过引入二维图像处理的连通区域标记法对同种类型的点云数据进行分割,并根据概率统计法和点云曲率特性,识别连通区域特征面点云的所属特征曲面类型。
1 点云模型特征面
1.1 微分信息估算
1.1.1 法向量估算
法向量是点云的重要属性之一,点云法向量的有效估计是点云分割的基础。点云法向估计方法可分为局部邻域拟合法和Voronoi/Dalaunay方法两类[9]。局部邻域拟合法在点云法向量估算中应用比较广泛,由文献[10]提出,称之为主成分分析法,该方法能快速有效地估算光滑曲面的法向量,但当曲面包含尖锐特征时估算的法向量不准确。一般来说产品的CAD模型是由多个基面组成的复杂模型,在多个基面交界的区域(特征区域)主成分分析方法估算的法矢被平滑,为了更准确地估算点云法向量,研究人员提出了许多改进方法[11-13]。其中,文献[11]所提方法能快速、准确地估算包含尖锐特征复杂模型的点云法矢,且参数具有自适应性,无需人工设置参数。本文采用文献[11]的方法进行法矢估计。
给定点集X={x1,x2,…,xN},其中,N为点云总数,任意一点xi的最近k邻域表示为Nb(xi),文献[11]对点xi的k邻域拟合的平面表示为:
(1)
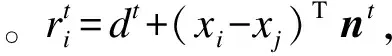
wr(ri)=exp(-(ri/σr)2),wn(ni)=exp(-‖ni-nj‖/σn2)和wn(xi)=exp(-‖xi-xj‖/σd2)分别为邻域点对当前点的残差、法向偏差和距离高斯权重,σd、σr和σn分别是距离、残差和法矢偏差带宽,用来控制各邻域点对当前点作用的大小。式(1)可以转化为对式(2)中半正定协方差矩阵C进行特征值分解。
(2)
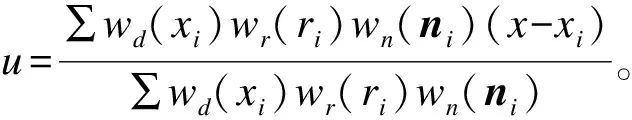
C可以分解为3个特征向量v2、v1和v0,3个特征向量对应的特征值分别是λ2,λ1,λ0,其中,λ2≥λ1≥λ0。最小特征值对应的特征向量为平面的法向量,即点xi的法向量ni=v0。
通过分解式(2)得到的法向量方向不一致,为了后续计算需要,把各点的法向量方向调整为一致方向。本文采用最小成本路径传播方法进行法矢方向调整[10]。图1是2种不同模型法矢估算和方向调整的结果,参数t=5,图中估算的法矢与相应局部面近似垂直。

图1 2种不同模型散乱点云法向量估算结果
1.1.2 离散点云曲率估算
通过法矢计算和方向调整,获得了比较准确的法矢。以法矢为邻域曲面的局部支撑,即可通过邻域构造离散点的局部参数化曲面,从而对离散点估算其曲面特性参数。
设待拟合邻域曲面为z(u,v),通过Tylor级数展开,去掉高阶无穷小,即可获得近似曲面表达式:
z(u,v)=TA,d(u,v)+O(d+1)
(3)
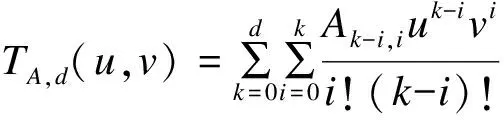
本文构造4次曲面估算点云曲率,曲面Tylor表达式为:
z(u,v) ≈TA,4(u,v) =
A0,0+ (A1,0u+A0,1v) +
(A2,0u2+2A1,1uv+A0,2v2)/2 +
(A3,0u3+3A2,1u2v+3A1,2uv2+A0,3v3)/6+
(A4,0u4+4A3,1u3v+6A2,2u2v2+
4A1,3uv3+A0,4v4)/24
(4)
引入新的矢量表达式:
P= (1,u,v,u2,uv,v2,u3,u2v,uv2,v3,u4,u3v,u2v2,uv3,v4)
则4次参数曲面可表示为如式(5)所示的矩阵形式。
PTQ=Z
(5)
其中,矩阵P中的u,v值为局部坐标系下的(u,v)参数,Q为待定系数Ak-i,i构成的矩阵,Z为局部坐标系下的z坐标值。将点及其邻域点的坐标(ui,vi,zi)代入矩阵方程即可求出所有待定系数Ak-i,i。
求解曲面基本参数E、F、G和L、M、N,并构造Weingarten曲率矩阵W[14]:
(6)
Weingarten矩阵的特征值就是主曲率k1、k2,特征向量就是主曲率方向,由k1、k2直接求高斯曲率K和平均曲率H。
曲率推导过程中,平均曲率H与法矢向量正相关,因而其符号与法矢方向正相关。法矢实际是由曲率主方向叉乘而来,如果曲率在法矢方向调整之前就已计算,则在法矢方向调整后,曲率方向和符号也要进行相应调整。如图2所示,法矢n反向后,对应最小主曲率k1和最大主曲率k2应反向互换。由H=(k1+k2)/2关系式可知,平均曲率H也要变号,由关系式K=k1×k2知,在k1和k2均变号的情况下,高斯曲率K不变号。
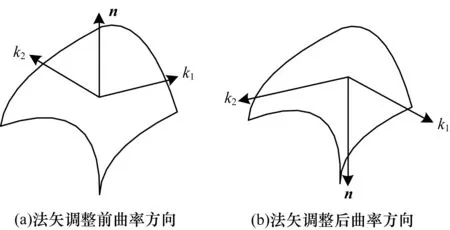
图2 曲率方向调整示意图
采用二次曲面法计算各点曲率,曲面坐标系在点的k邻域局部构建,各点之间的坐标构建相对独立,因而计算结果中的曲率值标准并不统一。根据点云分割需要,需对各曲率参数H、K、k1、k2进行归一化。同一物体的点云分割应采用同一判断标准,采用曲率法对点所属曲面类型进行判断,还涉及曲率零值和符号的确定问题,因而必须事先对所有点的曲率做全局归一化处理,并保证曲率在零值附近的分布规律不变。对此,本文采用零值对齐的归一化方法,从而保证了曲率数值符号的不变性。图3所示为4种归一化情况,其中M和m分别为曲率最大值和最小值,y为任一点曲率,不同情况的曲率归一化方法如下:
1)如果M>m>0,则置最大曲率为1,最小曲率为m/M,其他点的曲率按y=y/M计算。
2)如果M>0,m<0,M>abs(m),处理方法同第1种情况。
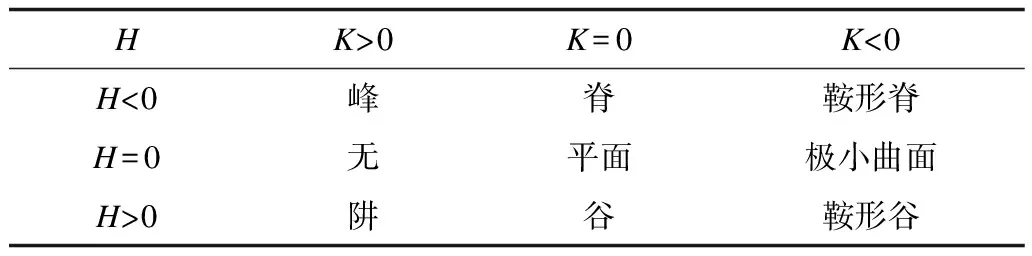
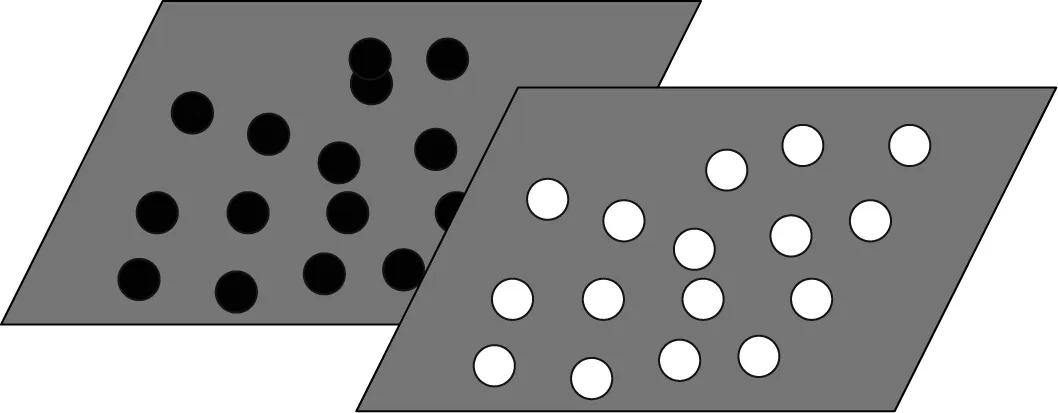
3)如果M>0,m<0,M 4)如果m 图3 不同情况曲率归一化示意图 1.2.1 点云初始聚类 基于离散点的高斯曲率K和平均曲率H,可以将点附近的曲面形状划分为峰、阱、脊、谷、鞍形脊、鞍形谷、平面和极小曲面8种类型,如表1所示。据此可将点云划分为8种类型,实现点云的初始聚类。 表1 曲面分类 高斯曲率由最小和最大主曲率乘积而得,会引入高阶误差,一般采用平均曲率作为上述划分的依据。在曲率归一化处理的前提下,根据表1的判断条件即可确定点所属面域特征。此时,曲率零值的设定将对曲面类型划分结果产生较大影响,本文处理方法是预设极小值e作为零值。经实验测定,推荐平均曲率H的零值阈值为[0.001,0.005],一般可预设eH=0.005,高斯曲率K的零值可按eK=eH/4设定,并将这2个阈值参数作为用户输入参数,便于调整。 1.2.2 点云连通区域分割 点云的初始聚类只是将所有离散点归属至8种曲率类型,但是同种类型的点云可能分属于不同的模型表面,如图4所示,黑色点集和白色点集都属于平面类型点,但是分别位于不同的面片,2个平面点集之间并不连通。因而,需要对同一种类型的点判断其连通性,将不连通的区域分割出来,实现点云的特征面分割。 图4 同种类型点云不连通情况示意图 从初始点云的角度看,2个分离区域必然存在邻域不连续的点,同一连通区域(局部相邻)内的点必定是全局相邻的。本文将二维图像处理中连通区域标记理论引入至三维点云区域分割[15],对三维点云连通性进行判断。 连通区域识别步骤如下: 1)当前点xi加入当前连通区域Ccidx_cur。 2)采用上述判断条件,对xi的局部邻域点xj进行全局连通性判断。 3)如果两者全局相邻,则判断xj是否已追加至其他连通区域Ccidx_merge,如果是则合并Ccidx_cur和Ccidx_merge。 4)否则,将xj加入当前连通区域Ccidx_cur。 经过连通区域分割后同种类型的面被分割成不同的块,需对各块点云进行特征面识别。 1.2.3 分块点云的曲面类型识别 CAD模型一般由规则型面组成,例如平面、圆柱面等规则特征曲面用于安装面、孔、倒角等加工特征,逆向工程中的特征面识别也主要是针对此类规则面。经过连通区域分析,已经获得分片点云,可以进一步展开典型造型面(平面、球面、圆柱面等)的类型判断。从统计角度上看,经分块后的点集同属一个曲面类型。因此,本文采用数学统计法对分块点云所属曲面类型进行判断,对区域点集中的点逐一判断其所属曲面类型,统计该区域中属于不同曲面类型的点的数目,将最大数目对应的曲面类型作为整个区域的曲面类型。 设xj为连通点云数据块X2∈X1中的任一点,Ti(i=0,1,2)对应平面、球面、圆柱面3类基本造型面,根据曲率条件,将点xj存入相应的类型数组Ti。3种特征面的判断条件如下: 1)平面:xj的最小曲率和最大曲率均等于0,即k1=k2=0,亦即K=H=0。如果过滤掉曲率突变点,则法矢夹角法更为直观,可优先识别平面。 2)圆柱面:xj的最小曲率等于0,最大曲率为常数,即k1=0,k2=C,亦即K=0,H=C。 3)球面:xj的最小曲率和最大曲率相等,即k1=k2=C=1/R,亦即K=1/R2,H=1/R(R为球半径)。 考虑到计算和浮点误差,在实际程序处理中,需对零值和两值是否相等的判断做特殊处理,预设极小值e,对零值和两值是否相等分别使用x 基于概率统计的曲面类型判断算法步骤如下: 1)对数据块X2中各点曲率做统计分析,获得曲率参数H、K、k1、k2的平均值和方差。 2)遍历X2中的所有点,按照点云所属曲面类型判断方法,将点划分至Ti。 3)统计Ti中的点数Ni,比值Ni/N即为当前区域属于面类型i的概率pi。 4)按标准正态分布3σ原则预设概率阈值pT(pT=0.68)。如果pi>pT,则认定当前聚类属于曲面类型i,返回曲面类型参数i。 使用VS2008和OpenGL开发平台,在Windows 10下分步实现了上述算法,并使用多种模型验证算法的有效性。实验所用的计算机的配置为CPU Intel Core i3 3.4 GHz,内存8 GB。 实验结果如表2、图5~图9所示。其中,在表2中,N为模型点云数量,面特征列第一个数字表示特征面类型(1-平面,2-圆柱面,3-球面),括号内的数字为该类型面的数目,r、eH分别表示曲率突变比例、平均曲率零值阈值。表中识别率表示算法对模型特征面所属曲面类型识别的正确率,是当前模型中正确识别的面片与总面片数的比值。图5~图9分别是模型1~模型5几种不同模型的分割和特征面识别结果。在计算参数中,模型2选用了较低的r值,是为了避免将部分圆柱面点纳入突变点,模型4选用较高的r值,以将前端沟槽处的棱线纳入突变点。此外,各模型的eH取值范围在[0.001,0.005]都能取得较好的分割效果。在接下来的点云识别计算中,规则模型1~模型3无过渡面,型面曲面类型全部正确识别,识别率达到100%,模型4除了过渡面之外全部正确识别,总体识别率达到95%,模型5除了过渡面未识别之外,其他面域识别均是正确的,主要型面的曲面类型识别率大于90%。面面相交实验显示,模型1~模型4的交线全部正确提取,模型5提取了主要平面与圆柱,以及圆柱与圆柱交线(相贯线)。此外,从计算效率来看,点云数量在50 000以下的模型各节点耗时都在0.65 s以内。 表2 参数设置及实验结果 图5 模型1点云分割与特征面识别结果 图6 模型2点云分割与特征面识别结果 图7 模型3点云分割与特征面识别结果 图8 模型4点云分割与特征面识别结果 图9 模型5点云分割与特征面识别结果 本文提出基于连通区域标记和统计法的散乱点云特征面分割与识别方法,在准确估算点云法矢的基础上,以估算的法矢作为4次曲面曲率局部坐标系的坐标轴。根据点云的曲率特性分析曲面的型面并进行点云预分割,引入二维图像处理中的连通区域标记法对点云连通区域分割,并采用统计法对点云所属特征类型面进行判断。实验结果表明,该方法能够取得较好的点云分割和识别效果。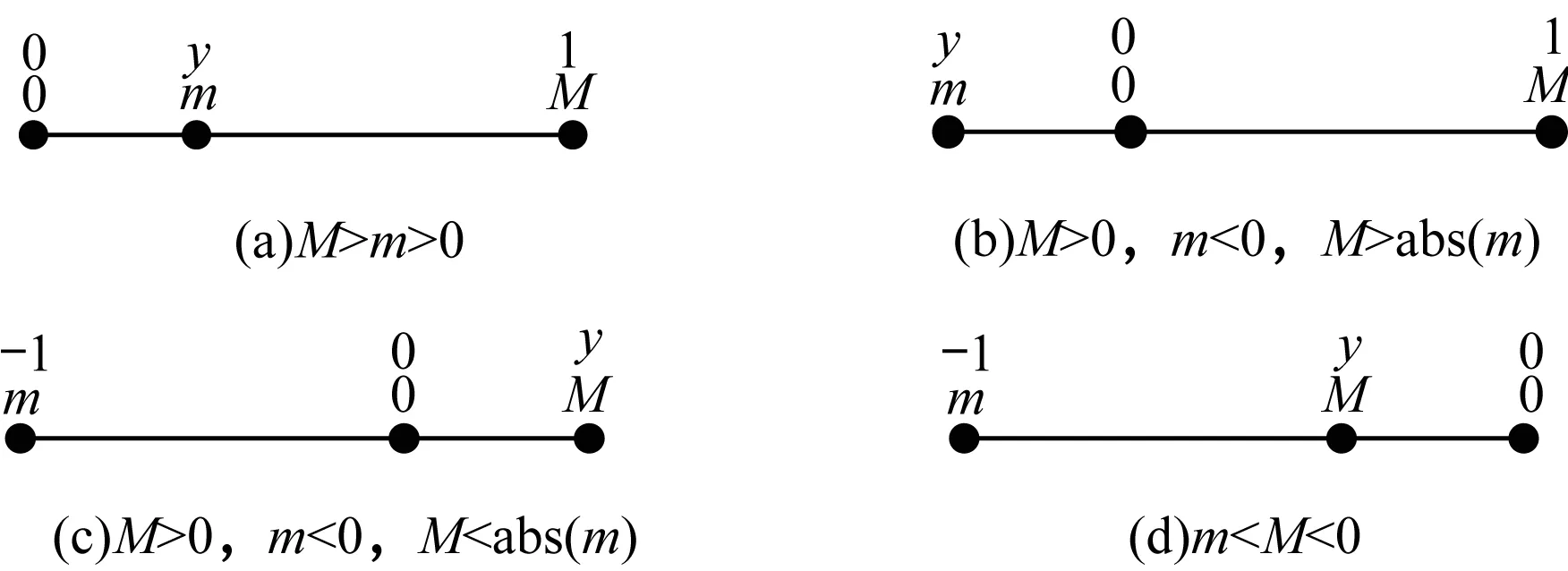
1.2 特征面的分割与识别
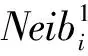
2 实验与结果分析





3 结束语
