基于迭代加权L2/L1范数块稀疏信号重构的ISAR成像算法
2018-11-20冯俊杰
冯俊杰,张 弓
(1.南京航空航天大学 电子信息工程学院,南京 211106; 2.六盘水师范学院 电气工程学院,贵州 六盘水 553004)
0 概述
逆合成孔径雷达(Inverse Synthetic Aperture Radar,ISAR)成像主要以电磁波作为发射信号,具有全天时、全天候、远距离探测目标和获取场景信息的能力,该项技术在军事、民用等领域占有极其重要的地位[1-4]。在通常情况下,利用发射大带宽信号可以提高距离向分辨率,通过增加目标转动积累角或长相干处理时间间隔(Coherent Processing Interval,CPI)来提高方位向分辨率。但是,当回波脉冲数有限或回波脉冲受到较强干扰时,很难达到理想的成像效果。另外,较长的CPI需要较复杂的补偿算法,这会给后续处理带来很大困难,且难以实现实时成像。因此,实现短观测时间高分辨率ISAR成像具有重要意义。
在信号处理领域,压缩感知(Compressive Sensing,CS)理论受到研究者的广泛关注[5-6]。在雷达目标成像中,目标一般由强散射点组成,这些强散射点在成像区域内是稀疏分布的,即目标相对于成像背景表现出高度的稀疏性。因此,利用压缩感知理论可以改进雷达成像质量,该方法的典型代表有SAR成像[7-8]、ISAR成像[9-10]、MIMO雷达成像[11-12]等。
由于天空成像的背景目标实际轮廓和成像区域相比较小,目标具有稀疏结构。传统稀疏信号重构雷达成像是在每个距离单元上利用稀疏信号重构算法来重构强散射点信息。实际上,由于目标是一个整体,目标散射点间并非独立存在,而是具有块状或者簇状结构特征。传统稀疏信号重构雷达成像算法仅考虑目标散射点的稀疏性,因此,不能完整地刻画块状目标的真实结构。文献[13]提出二维结构模式耦合贝叶斯(PC-SBL)ISAR成像算法,但该算法运算量较大、复杂度较高。
为解决上述问题,本文利用ISAR目标潜在的块状稀疏结构,针对在实际应用中信号块稀疏度未知的情况,提出一种迭代加权L2/L1范数块稀疏信号重构ISAR成像算法,以实现快速、高分辨率ISAR成像。
1 ISAR成像模型
假设目标位于远场,发射线性调频信号为:
(1)
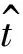
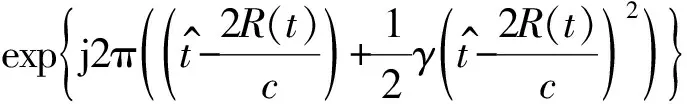
(2)
其中,A为散射中心复散射系数,Ta为CPI,λ=fc/c为波长,c为光速,R为目标距离。进行距离脉冲压缩后,接收到的信号为:
(3)
其中,f=2xω/λ为多普勒频率,β=2xα/λ为多普勒调频率,ω和α分别为旋转角速度和角加速度。假设距离单元R0+y内包含K个距离强散射点,忽略散射时变性,此单元的回波信号为:
(4)
其中,fk和Ak分别为第k个散射中心的多普勒频率和复散射系数,n为噪声。由式(4)可以看出,信号主要由少量的强散射点表征。定义时间和多普勒频率分辨间隔分别为Δt和Δfd,脉冲重复频率为fr,则时间序列为t=[1∶N]·Δt,Δt=1/fr,N=Ta/Δt对应脉冲次数。多普勒向量为fd=[1∶Q]·Δfd,Q=fr/Δfd,构造稀疏基矩阵Φ={φ1,φ2,…,φQ},其中,φq(t)=exp(-j2πfd(q)t),0≤q≤Q。式(4)可以写为:
y=Φx+n
(5)
散射系数向量x包含了强散射点信息,为稀疏向量。将求解x的问题转化为下列优化问题:
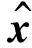
(6)
其中,ε为一较小常量,其值与噪声方差有关。
2 迭代加权混合L2/L1范数块稀疏信号重构
考虑块稀疏信号:
(7)
基于L2/L1优化模型的块稀疏信号重构问题描述为:
s.t.‖y-Φx‖2<τ
(8)
本文采用迭代加权L2/L1范数来重构块稀疏信号,迭代加权L2/L1范数最小化信号模型可以表示为:
s.t.‖y-Φx‖2<τ
(9)
式(9)为有约束的表示模型,不易求解。将其约束模型转化为无约束问题:
(10)

(11)

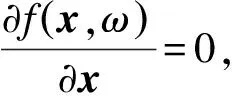
(ΦTΦx-Φy)+λW-1x=0
(12)
由于式(12)为非线性方程,无法直接对其求解。因此,采用迭代加权算法来估计块稀疏解。当前迭代的权值由上次迭代获得的块信号估计值决定,则第l+1次迭代时的稀疏解为:
x=[ΦTΦ+λW-1]ΦTy
(13)
迭代加权混合L2/L1范数块稀疏信号重构算法步骤如下:
步骤1初始化。
1)令迭代次数l←1,辅助变量初始化ε←ε0。

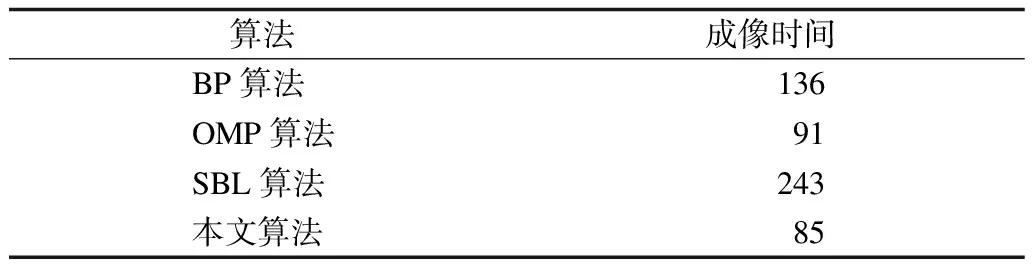
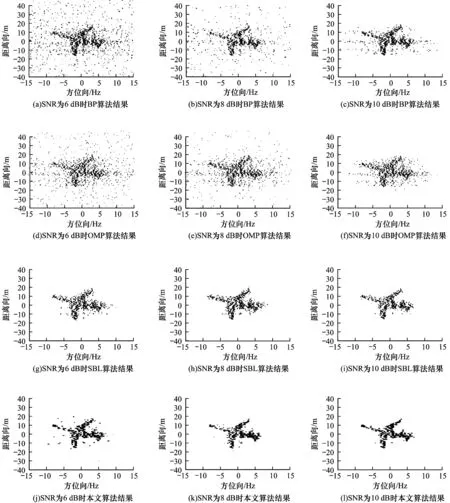
步骤2当l 1)更新非零权系数: 2)更新目标参数: 3)更新参数ε: 4)l←l+1。 参数ε为一较小的常量,它用来避免当加权向量中出现零元素值时导致算法运行终止现象。为进一步改善算法的稳定性,逐渐减小参数ε,即在刚开始几次迭代中使用较大的ε值,然后逐渐减小,直到满足迭代终止条件。块稀疏信号权值根据前一次迭代过程中得到的原始信号估计值来进行选取。 本次实验数据为ISAR系统录取的Yak-42飞机实测回波数据,雷达参数为:信号频带宽度为400 MHz,中心载频为5.52 GHz,数据脉冲重复频率(Pulse Repeat Frequency,PRF)为100 Hz,脉冲宽度为25.6 μs。在不同脉冲数条件下,将BP算法[14]、OMP算法[15]、SBL算法[16]和本文算法成像结果进行比较。抽取16个脉冲、32个脉冲和64个脉冲分别进行实验,结果如图1所示。 图1 4种算法在不同脉冲数时的ISAR成像结果 从图1可以看出,随着脉冲数的增加,4种算法的成像质量逐渐提高,在脉冲数为16时,BP算法重构图像变得模糊,SBL算法和OMP算法出现虚假散射点。本文算法由于考虑目标的块状结构特征,无论脉冲数为多少,都能使图像中的飞机保持较好的轮廓,即具有较好的成像效果。在脉冲数为32时,每种算法重复100次实验,平均成像时间如表1所示。从表1可以看出,本文算法成像所需时间少于其他3种算法,表明其有利于实时成像。 表1 4种算法成像时间比较 s 本次实验通过在原始回波数据中加入复高斯白噪声来设置不同的信噪比(Signal-to-Noise Ratio,SNR)。图2所示为4种算法在信噪比分别为6 dB、8 dB、10 dB三种情况下的成像结果。 图2 4种算法在不同信噪比时ISAR成像结果 从图2可以看出,在较高SNR条件下,各算法均可得到较好的成像结果。但随着SNR下降,BP算法和OMP算法的成像结果受噪声影响严重,成像性能下降。当信噪比为6 dB时,BP算法和OMP算法的图像出现了较多的虚假散射点,而SBL算法和本文算法虚假散射点很少,能够较好地呈现目标的特征。 ISAR目标在距离-多普勒平面具有块稀疏特性,其稀疏散射点并不是随机分布的。本文根据目标的块状结构特征,结合信号加权优化思想,提出迭代加权L2/L1范数块稀疏信号重构ISAR成像算法。仿真结果表明,相比BP、OMP、SBL算法,该算法可以在提高重构效率的同时改善成像质量。下一步将对权值进行研究,以提高本文算法在噪声环境中的成像性能。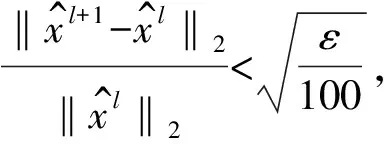
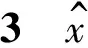
3 仿真结果与分析
3.1 脉冲个数对成像结果的影响

3.2 信噪比对算法性能的影响
4 结束语
