PMUS-HOSGD张量分解方法及其在标签推荐中的应用

杨 林,顾军华,官 磊,张宇娟,彭玉青

(河北工业大学 a.计算机科学与软件学院; b.河北省大数据重点实验室,天津 300400)

0 概述

随着信息技术和互联网的发展,互联网使用者从信息匮乏的时代步入了信息过载的时代,用户的个性化需求也越来越大。用户的个性化特征注重的是用户的参与,用户可以对资源(视频、歌曲、图片等)赋予自定义的标签,逐渐形成Folksonomy的大众分类法[1],该分类法不仅可以获取并分析用户的兴趣特征,而且在一定程度上丰富了资源的描述信息。随着网络资源规模爆发式的增长[2],用于标注的标签越来越多,用户面对大量的数据如何选出自己需要的标签越来越困难。解决信息过载的有效方法是个性化推荐[3],由此基于社会标注系统的标签推荐服务应运而生。例如,给书籍和视频提供短评的豆瓣网、论文书签网站CiteULike和视频推荐网站MovieLens等都是利用社会标注系统对资源进行标注,然后通过标签推荐系统将用户感兴趣的标签推荐给用户。推荐系统简化标注过程,方便用户,提高了标签的质量和标注的准确性。

标签推荐系统的核心是构建“用户-资源-标签”三维数据,挖掘数据之间的潜在关系,从而准确的为用户推荐标签。目前,针对标签推荐系统已经展开了大量的研究。文献[4-5]将三维关系拆成“用户-资源”、“用户-标签”和“资源-标签”3个二维矩阵,使用协同过滤算法进行处理。文献[6]受Google的PageRank算法[7]启发提出FolkRank算法,同样将三维关系拆分成3个二维关系。但是这些方法破坏了高维空间数据原本的特征结构,丢失了三者之间的协同关系。为解决这个问题,挖掘“用户-资源-标签”之间潜在的语义关联,文献[8]提出使用三维张量存储“用户-资源-标签”数据。

在构建初始张量阶段,目前使用最多的方法是用“0/1”构建张量,这种方法构建容易,可读性强,但是不能体现出标签在资源中的差异。文献[9]发现由于热门标签通常有较大的权重,导致推荐结果偏向于热门标签,反而降低推荐的准确率。文献[10-12]提出使用TF-IDF来设置惩罚项,用以区分标签对资源的重要程度,可以减少热门标签对结果的影响。然而上述方法都忽略了用户对资源的偏好程度。

对构建完成的张量进行分解,可以挖掘张量包含的潜在信息。文献[13]将奇异值分解方法推广到三维张量,提出高阶奇异值分解(Hign Order Singular Value Decomposition,HOSVD)方法对张量进行分解,该方法保留了三者的关联信息。文献[14]基于矩阵奇异值分解能有效地平滑数据矩阵中的数据特点,在使用HOSVD进行分解的过程中,结合用户朋友关系修正张量分解结果,建立张量分解模型。文献[15]提出新的推荐算法PITF(Pairwise Interaction Tensor Factorization),该算法在张量分解的过程中加入3个二维关系之间的潜在联系,推荐质量得到提高。针对目前推荐系统存在的稀疏性问题,文献[16]在CubeSVD[17]的基础上进行改进,使用ALS算法进行矩阵分解,提出CubeALS推荐算法,该算法有效提高了稀疏数据标签推荐的准确性。文献[18]提出一种基于上下文学习和张量分解的个性化推荐算法,将用户和项目的上下文信息加入2个张量中,有效改善数据稀疏性。文献[19]提出一种改进的基于张量分解的推荐算法,引入基于标签综合共现的谱聚类方法,使用HOSVD-HOOI算法对初始张量进行分解,进一步优化推荐效果。目前的张量分解方法多数以SVD为基础进行改进。使用SVD方法对张量的每个维度矩阵进行分解,虽然在一定程度上提高了推荐的准确性,但由于构建的初始张量极其稀疏,需要在分解前对初始张量的展开矩阵进行填充,这样存在2个问题:1)填充过程增加数据量,同时增加算法复杂度;2)简单的数据填充易造成数据失真,从而影响推荐结果的准确度。

针对上述问题,本文结合PMUS(Penalty Mechanism-User Score)张量构建方法与HOSGD(High Order Stochastic Gradient Descent)张量分解方法,提出PMUS-HOSGD算法对“用户-资源-标签” 三维数据进行处理,为用户推荐个性化标签。本文主要工作如下:1)在张量构建阶段,提出惩罚机制与用户评分相结合的张量构建方法PMUS来计算标签的权值;2)在张量分解阶段,提出基于随机梯度下降(Stochastic Gradient Desecent,SGD)的高阶张量分解方法HOSGD。

1 相关工作

1.1 张量及其矩阵展开

张量由多维数据组成,是一个N维的向量空间,一维张量是一个向量(Vector),二维张量是一个矩阵(Matrix),三维或者更高维的张量则是高维张量(Tensor)。标签推荐系统使用三维张量存储数据,3个维度分别代表用户、资源、标签。

使用aijk表示三维张量的值,其大小代表用户i给资源j标注标签k的概率。例如,用户1给资源1标注了标签2,则对应张量中的值为a112=1,其余的标注0。

矩阵展开是将一个张量的元素重新排列(即对张量的不同维度进行重新排列),得到一个矩阵的过程。三维张量A∈RI1×I2×I3在第n维度上的展开矩阵表示为X(n)∈RIn×(I1×I2×…×In-1×In+1×…×IN)。

1.2 张量分解

基本的张量分解算法HOSVD需要对张量A每个维度(n=1,2,3)的展开矩阵进行SVD分解,计算公式是:

(1)

通过上述公式对An进行奇异值分解,分别得到3个维度的展开矩阵的U矩阵和奇异值矩阵S。

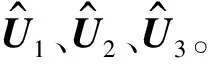
张量与矩阵的模积定义为一个张量X∈RI1×I2×…×IN和一个矩阵U∈RJ×In的n-mode乘积(X×nU)∈RI1×I2×…×In-1×J×In+1×…×IN,其元素定义为:

(2)

如果J

(3)

(4)

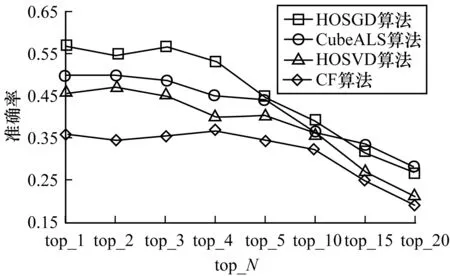
2 PMUS-HOSGD张量分解方法

传统的张量分解算法HOSVD可以挖掘“用户-资源-标签”三维数据之间的关系,但在实际应用中,用户仅对个别资源进行标签标注,这会导致张量中的数据极度稀疏。目前常用的HOSVD算法在张量分解的过程前需要对稀疏矩阵进行填充,这样会造成数据的失真。因此,本文结合PMUS张量构建方法与HOSGD张量分解方法,提出PMUS-HOSGD算法对 “用户-资源-标签” 三维数据进行处理,为用户推荐个性化标签。

2.1 PMUS初始张量构建

在“用户-资源-标签”三维张量中,“0/1”构建方法简单易行,但是标签之间没有区分度,因此可以使用PMUS的思想计算标签的权重;同时,用户对资源的评分可以体现出用户对资源的偏好程度,用标签的权重乘以评分可以很好地区分出标签之间以及用户和资源之间的重要度,最终构建整个张量。

PMUS的主要思想是:如果一个标签在一个资源中出现多次,并且在其他资源中很少出现,则可以认为该标签具有很好的区分度,同时如果一个用户给资源的评分越高,用户对这个资源的偏爱程度越大,则给这个视频标注的标签的概率就越大。

使用PMUS计算标签权值的过程如下:

1)计算标签t对于资源i的重要度import(t,i),针对每个资源都有一个标签权重向量,公式如下:

(5)

2)根据重要度(import)计算标签t在用户u对资源i标注的标签集中占的比例权重weight(u,t,i),公式如下:

weight(u,t,i)=import(t,i)/sum_weight(u,i)

(6)

其中,sum_weight(u,i)是用户u给资源i标注的所有标签的重要度的总和。

3)weight(u,t,i)乘以用户u给资源i的评分就是张量中用户u在资源i中使用标签t的权值Value(u,t,i),公式如下:

Value(u,t,i)=weight(u,t,i)×score(u,i)

(7)

2.2 基于随机梯度下降的张量分解算法HOSGD

传统的SVD算法对二维矩阵进行分解,可以求出对应的特征矩阵,随着用户数量、资源数量和标签数量的急剧增长,SVD分解带来的误差和复杂度也在不断增加,正是由于这些问题,Simon Funk发表了一个只考虑已有评分的矩阵分解方法,称为Funk-SVD,也就是被文献[20]称为隐语义模型的矩阵分解方法,该方法使用梯度下降法(Gradient Descent,GD)最小化训练集中观察值的RMSE(Root Mean Squared Error),在二维矩阵分解中取得了较好的推荐效果。

标准的梯度下降法在更新变量前要对所有的样本计算误差并汇总,导致算法收敛速度较慢,因此本文使用随机梯度下降法,SGD是在梯度下降法的基础上,在迭代过程中使用部分样本计算梯度,因此其比标准梯度下降法有更高的收敛速度。

借鉴SGD在二维矩阵分解领域中的应用,本文提出HOSGD张量分解算法。HOSGD算法在张量进行分解的过程中,为提高准确性,使用SGD算法对展开矩阵分解,降低了传统分解方法带来的计算复杂度及误差。

在用户给资源标注标签的过程中,形成了若干{用户,资源,标签}数据,使用PMUS方法构建利用式(5)、式(6)和式(7)计算Value(u,t,i),得到三维张量A∈RX×Y×Z,HOSGD算法对张量的展开矩阵进行SGD分解,得到3个特征矩阵,进而计算出初始张量的核心张量,然后可以得到初始张量的近似张量。算法描述如下:

算法1PMUS-HOSGD张量分解

输入用户、资源、标签数据三元组(u,i,t)

输出初始张量的近似张量

1.使用PMUS方法按照式(5)、式(6)、式(7)计算标签的权值

2.使用张量A存储式(7)计算得到的Value(u,t,i)

3.将张量A按照3个维度展开得到A1、A2、A3

4.for i=1 to 3

5.按照算法2对Ai进行处理,得到P1、P2、P3

6.end for

在算法1中,对于三维张量A∈RX×Y×Z,其中,用户、资源和标签的数量分别为X,Y和Z,初始张量A展开得到的3个矩阵A1、A2、A3的规模分别为X×YZ、Y×XZ和Z×XY,按照算法2,分别对A1、A2、A3进行分解,得到每个维度的特征矩阵P1、P2、P3,其中P1∈RX×k1,P2∈RY×k2,P3∈RZ×k3,3个特征矩阵的特征数k1、k2、k3是根据数据规模设定的,一般ki<

(8)

(9)

其中,左边第1项是误差项,用原始矩阵中有值的项减去P和Q对应行和列相乘得到的值,左边第2项是正则化项,防止过拟合。对L最小化就得到了P和Q。

通过式(8)分别对PU和QI求其梯度:

(10)

(11)

其中,λ表示正则化参数,A(U)表示矩阵A第U行中不为0或者空的列,A(I)表示矩阵A第I列中不为0或者空的行,通过矩阵A第U行,可以得到矩阵P第U行的梯度,也就是PU需要更新的值:

(12)

(13)

其中,α表示步长,对矩阵P中所有的PU进行更新,或者对Q矩阵中所有的QI进行更新,就完成了一次迭代,在每次迭代的过程中,实现了P和Q矩阵的一次更新,损失函数L的值减小。算法描述如下:

算法2基于SGD的张量展开矩阵分解

输入张量的展开矩阵Ai

输出Ai的特征矩阵P

4.步骤2和步骤3是一次迭代的过程,多次执行步骤2和步骤3,不断更新PU和QI的值,直到完成迭代次数t或者误差小于阈值,得到P和Q的最优解

在算法2中,λ和α参数需要在实验中多次调优得到。算法的核心在于每次更新PU和QI时只使用原始矩阵中有值的部分,得到P和Q的最优解,P即为对应的特征矩阵。

PMUS-HOSGD张量分解方法的时间复杂度主要是在对每个维度展开矩阵的分解基础上进行计算的。算法2矩阵分解的时间复杂度是O(t×X×k1×n1′),据此可得算法1的时间复杂度是O(t×(X×k1×n1′+Y×k2×n2′+Z×k3×n3′)),其中,t为迭代次数,k为特征数,n′是矩阵中平均每行非空数据的数目。

3 实验结果与分析

本文使用相同的数据集和评价标准对比张量构建方法和张量分解方法,采用常用的评价指标验证算法的有效性。

3.1 数据集

本文使用MovieLens数据集,包含用户对视频的评分,以及用户给视频标注的标签数据。

使用MovieLens数据集构建的三维张量极其稀疏,因此对初始数据进行预处理,预处理后的数据中每个用户都对15个或15个以上视频打过标签,每个视频都由15个或15个以上用户打过标签。处理后的数据中用户、视频、标签的数量分别是184、122、378,有20 149条“用户、资源、标签”数据。

3.2 评价标准

本文使用准确率(Precision)、召回率(Recall)和F值[21]作为算法的评价标准。在推荐系统中,准确率表示在推荐列表中得到的推荐结果与测试集中实际情况相同的物品数与所有的推荐物品数的比值,召回率指的是推荐列表中准确的结果占测试样本的比例。在实验过程中,将预处理后的数据集分成2部分:训练集和测试集,其中,训练集占75%,测试集占25%。

准确率和召回率的计算公式如下:

(14)

(15)

其中,test表示测试集,top_N表示推荐的结果,N表示推荐的数目,准确率和召回率的值越高推荐效果越好。

F值作为常用评价指标,能更好地反映推荐结果的效果,F的值越高推荐效果越好。

(16)

3.3 实验结果

为验证PMUS方法构建张量能提高推荐结果的准确率,实验结合使用HOSVD分解算法,分别对比“0/1”、TF-IDF和PMUS张量构建方法的准确率、召回率和F值。实验结果如图1～图3所示,每个图中各有3条曲线,分别代表“0/1”、TF-IDF和PMUS张量构建方法结合HOSVD分解方法的实验结果,每条曲线有8个节点,横轴代表top_N的值,纵轴分别代表准确率、召回率和F值。

图1 3种构建方法的准确率比较

图2 3种构建方法的召回率比较

图3 3种构建方法的F值比较

由图1～图3中3种不同构建方法的对比可知,在top_1时,使用“0/1”构建的张量进行分解推荐的准确率比PMUS和TF-IDF方法要好,但是随着N的增长,PMUS方法构建的张量的准确率要高于其他2种算法,比TF-IDF平均高0.03。在推荐数量小于10时,PMUS方法构建张量的召回率和F值要明显高于其他2种方法,说明使用PMUS方法构建张量,张量权值在加入标签对视频的权重以及用户对视频的评分后,使用户对视频标注的标签权值更加真实。在实际推荐系统中,给用户推荐的少量标签不止1个,因此使用PMUS方法构建张量得到的推荐结果要优于普通的“0/1”和TF-IDF构建方法。

为进一步验证HOSGD推荐算法的性能,本文结合使用PMUS方法构建张量,对HOSGD与HOSVD、协同过滤(Collaborative Filtering,CF)和CubeALS 算法进行了对比。基于CF的标签推荐算法是目前应用比较广泛的个性化推荐算法;HOSVD是一种经典的张量分解算法,被大量的应用于三维数据推荐领域,而且取得了良好的实验结果;CubeALS推荐算法与其他优秀的算法对比,推荐效果有显著提高。

在用HOSGD分解展开矩阵的过程中,涉及到步长α、正则化系数λ、特征因子数目k、迭代次数和阈值5个参数。α过大可能会导致迭代不收敛,从而发散,因此α分别取0.01、0.05、0.1、0.2、0.3、0.6进行对比;k数目过多会导致收敛速度慢,程序时间复杂度高,因此特征因子k数目取10到20进行对比。通过多次实验,发现在迭代50次左右误差结果接近0.08,趋于稳定。结合实验结果,张量分解中取步长α为0.2,正则化系数λ为0.000 3,特征因子k数目为17,迭代50次,阈值为0.08。实验结果如图4～图6所示。由图4～图6可知,4种算法的准确率呈下降趋势,HOSGD的准确率在top_N小于5的情况下均高于其他算法,尤其在top_1至top_4阶段HOSGD的准确率平均比CubeALS提升0.07。在top_1至 top_5阶段HOSGD的召回率和F值也明显高于次优的CubeALS算法。在实际推荐系统中,给用户提供1-5个标签,HOSGD算法符合实际要求。实验结果表明,使用随机梯度下降的张量分解算法HOSGD能够充分利用SGD方法的优势,有效处理稀疏张量,减少误差。

图4 4种推荐算法的准确率比较

图5 4种推荐算法的召回率比较

图6 4种推荐算法的F值比较

综上所述,使用PMUS构建张量并结合使用基于随机梯度下降法的HOSGD进行张量分解的PMUS-HOSGD算法,可以有效提高标签推荐的准确率。

4 结束语

在个性化标签推荐领域,使用张量存储“用户-资源-标签”数据是一种很好的数据表示形式,但由于三维数据的稀疏性,传统的张量构建方法和张量分解方法的推荐准确率较低。因此,本文利用PMUS构建张量,并结合基于随机梯度下降法的HOSGD对张量进行分解。实验结果表明,与 HOSVD、CF和CubeALS算法相比,PMUS-HOSGD算法具有更好的推荐效果。下一步将重点研究在大数据量的情况下如何提高推荐速度,并使用分布式平台运行该算法。