爆炸作用下冻结管振动响应规律研究
2018-11-20种玉配张帅军白中坤东兆星齐燕军
种玉配,张帅军,白中坤,东兆星,齐燕军
(1.中铁隧道局集团有限公司勘察设计研究院,广东 广州 511400;2.中国矿业大学力学与土木工程学院,江苏 徐州 221116;3.中国矿业大学深部岩土力学与地下工程国家重点实验室,江苏 徐州 221116)
随着我国工业化进程的加速,经过几十年的大规模开采,埋深较浅的煤炭资源已经枯竭殆尽。目前在建矿井不可避免的达到上千米的深度,需穿越深厚的表土层和含水基岩段。在这种复杂的地质条件下,冻结法凿井成为我国立井特殊施工的首选技术。在冻结法凿井过程中,一旦冻结管发生断裂,盐水泄露造成冻结壁直接受到盐水的侵蚀,轻则造成冻结井壁融化,使得施工无法继续进行,重则发生淹井事故,造成重大的经济损失。为此,研究爆炸作用下冻结管振动响应规律对指导井筒冻结基岩段的冻结、爆破掘进设计与施工和冻结管断裂信息预测均有重要科学价值和现实意义。目前,国内外学者针对不耦合装药结构已经做了大量研究。崔广心等[1]、杨维好等[2]利用相识理论与模型试验分析了冻结管在安装阶段和掘进阶段受到的弯曲、温度应力。马芹永[3-4]基于冻结压力、爆破冲击压应力、冻结管温度应力提出了冻土爆破作用下冻结管强度准则。经来旺等[5-6]根据温度应力、冲击压应力、弯曲应力、冻结压力和摩擦力对冻结管进行计算,提出了冻结管最容易发生破裂的位置。陆卫国等[7]总结井筒冻结管断裂的主要原因,提出了深厚冲积层冻结管断裂的防治措施。周晓敏[8]采用复合三角函数曲线逼近挠度曲线近似求解冻结管的内力分布,研究了冻结管受力非线性微分关系。姜玉松等[9]通过模型试验分析了冻结管应力与起爆药量、距离的关系。以上学者对冻结管的断裂应力场与位移进行了理论分析,如温度应力、弯曲应力、摩擦应力和冻土盐水压力等,这些大都是在静力作用下及表土层中研究冻结管受力状态与断裂原因,对于爆炸作用下基岩段中冻结管的振动响应规律研究仍然较少。
基于现有的科学研究成果,以内蒙古鄂尔多斯地区某矿冻结副立井爆破开挖为工程背景,通过坐标变换求得爆炸应力波在冻结管周围散射场,采用ANSYS/LS-DYNA模拟不同冻结温度和不同起爆药量下,冻结管的振动响应规律,为立井的冻结与爆破施工提供参考。
1 工程概况
依托内蒙古鄂尔多斯地区某煤矿冻结凿井工程,该煤矿的年设计生产能力为12 Mt。副井为立井,净直径为10 m,使用全井冻结方法。从井筒检查孔的地质情况来看,井筒穿越岩层岩性有中砂、细粒砂岩、细砂、粉砂、中粒砂岩和粉质泥岩。井筒冻结基岩段使用的是钻爆法施工方法,采用伞钻(SJZ-8A型)配凿岩机(YGZ-70型)凿岩。采用T220型防冻水胶炸药和抗杂散电雷管,脚线的长度为6.5 m,5段毫秒延期起爆总延迟时间不大于130 ms。地面动力电源起爆,反向装药结构,掏槽眼和辅助眼的药卷直径为45 mm,爆破原始条件见表1。
2 爆炸应力波在冻结管周围的散射
通常情况下,在装药直径的4~5倍距离范围之外可以将爆炸应力波简化为平面波,因此在实际工程中将爆炸应力波近似为平面波处理。因为横波波速小于纵波波速,所以在岩土介质中将爆炸应力波近似简化为纵波[10]。
如图1所示,管道内半径为c,外半径为d。

表1 井筒爆破原始条件

图1 P波入射冻结管示意图
假设入射波是一个频率为w的稳态P波[11],那么该稳态入射波的φr就能够表示为式(1)。
φr=φ0exp{ikIf,s(xcosα+ysinα)}e-iwt
(1)

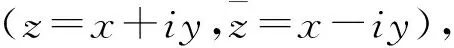
(2)
式中,符号意义同上。
在入射波的作用下,冻结管内存在着由冻结管外边界向冻结管内部传播的折射波和在冻结管内边界向外传播的散射波,折射波和散射波可以用Hankel级数展开式表示,因此,冻结管内的总波场表示为式(3)。
(3)
式中:Π表示冻结管内的量;f表示为折射波场;其他符号意义表达式见式(4)~(7)。
(4)
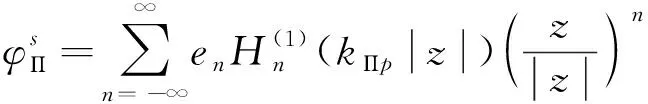
(5)
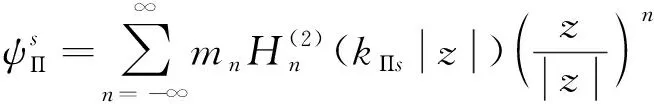
(6)

(7)

应用转轴公式,建立冻结管位移和应力的复数形式。在坐标变换之后的位移场的复数形式见式(8)~(9)。
(8)
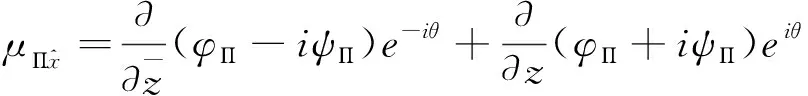
(9)
坐标变换之后的应力场的复数形式见式(10)~(11)。

(10)
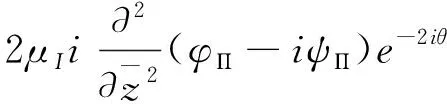
(11)
式中:Π为下标,为冻结管内的量;其余符号意义同上。
3 爆炸作用下冻结管振动响应规律
目前,ANSYS/LS-DYNA有150多种非金属材料模型和金属材料模型,其中包括隧道岩石爆破所涉及到的炸药、岩石、空气、水和炮泥等多种介质。有14种状态方程用来解决各种复杂的材料特性与物理现象,合理的选择数值模拟中的材料模型和算法,可以提高数值模拟的精度,是高效模拟分析轴向不耦合装药结构爆破的关键。运用ANSYS/LS-DYNA对爆炸问题进行分析,一般有LAGRANGE、EULER和ALE三种算法。LAGRANGE算法在处理流体、气体等大变形问题时,节点单元的变形会降低计算速度而导致计算程序的终止。EULER算法相对很难定义边界条件,求解速度低于LAGRANGE算法。ALE算法允许材料随意流动和很好的定义边界条件,有效解决单元畸变问题和爆破多物质耦合问题。本计算模型涉及到炸药、围岩、空气、盐水和冻结管多种物质,采用ALE算法。
3.1 材料模型和性能参数选取
1) 在ANSYS/LS-DYNA中,*MAT_HIGH_EXPLOSIVE_BURN高性能炸药材料关键字用于模拟炸药的爆轰[12]。*EOS_JWL状态方程用于描述炸药材料在爆炸时的压力特征,可以描述炸药爆炸产生的爆轰产物的压力、单位体积的内能和相对体积参数。*EOS_JWL状态方程的具体形式见式(12)。本次模拟使用炸药的具体参数见表2。
(12)
式中:P为炸药爆轰产物的压力;A、B、R1、R2、w分别为表征炸药特性的常数,与炸药的种类有关;V为相对比容,V=v/v0,v=1/ρ,v为比容,v0为炸药爆炸前的比容;E0表示炸药爆轰的初始内能。

表2 炸药及状态方程主要参数
2) 岩石的模型采用的是*MAT_PLASTIC_KINEMATIC,该材料模型是ANSYS/LS-DYNA中一种考虑了材料失效的各向同性或者随动硬化与应变率相关的模型,其各向同性与随动硬化之间的比重是通过调节硬化参数β来改变[13]。屈服应力与应变率之间的关系见式(13)。不同温度下饱水砂岩的相关力学参数见表3。
(13)

3) 空气可以选用*MAT_NULL模型,这种模型适用于气体或者流体材料,并且该材料模型允许状态方程在计算过程中忽略偏应力的影响。该材料模型需要同*EOS_LINEAR_POLYNOMIAL状态方程联合使用。表4为空气主要参数。
4) 冻结凿井工程中的冻结管多采用无缝钢管制作而成,因此冻结管的参数可以选择无缝钢管的材料参数。冻结管的材料模型选择为*MAT_JOHNSON_COOK模型,状态方程选择为*EOS_GRUNEISEN方程。冻结管及状态方程主要参数见表5。
5) 冻结管内的盐水可以选用*MAT_NULL模型,这种模型适用于气体或者流体材料,并且该材料模型允许状态方程在计算过程中忽略偏应力的影响,该材料模型需要同*EOS_GRUNEISEN状态方程联合使用,盐水及状态方程主要参数见表6。

表3 岩石主要参数

表4 空气主要参数

表5 冻结管及状态方程主要参数

表6 盐水及状态方程主要参数
3.2 计算模型与模拟方案
根据对称性原则,建物理模型如图2所示。建立数值模拟模型的尺寸如下:模型的半径为15 m,高度为4 m。药卷直径为32 mm,炮眼直径为42 mm,炮孔位于图2中坐标轴位置处即平面扇形圆心处,冻结管位于X坐标轴正向,距离炮孔中心水平距离为9 m,冻结管直径为168 mm,建立单孔柱状装药模型,单位制为cm-g-μs。模型上部采用自由边界,对称面施加边界约束,其余施加无反射边界条件,对计算模型中的岩石介质采用不等距网格,距离药柱越近网格就越密,距离药柱越远,网格就越稀疏。

图2 ANSYS模型示意图
结合实际工程背景以及所建立的模型,以50 kg起爆药量、-15 ℃温度和9 m距爆源距离参数为基准,研究不同冻结温度下(-10 ℃、-15 ℃、-20 ℃和-30 ℃),冻结管对爆炸作用的振动响应规律。
3.3 模拟结果与分析
图3为冻结管在不同温度下不同时刻的压力云图。
综合对比图3(a)~(h)可以发现, -10 ℃、-15 ℃、-20 ℃和-30 ℃开始出现压力值的时间分别为4 200 μs、3 600 μs、3 300 μs和2 700 μs,表明在相同的起爆药量以及相同的冻结管距爆源距离下,随着冻结温度的降低,冻结管对爆炸应力波的压力响应出现的时间不断减小,即冻结温度的降低导致爆炸应力波传播至冻结管的时间减小。温度变化使得岩体介质的力学参数发现改变,使得爆炸应力波在冻结岩体中传播速度发生变化,进而导致不同温度下冻结管开始出现压力的时间不一致。
将不同冻结温度下不同参考位置处冻结管的最大拉应力和最大压应力绘成曲线,如图4所示。
从图4可以看出,总体上随着冻结温度的不断增高,冻结管(背爆面中心、垂直面中心和迎爆面中心)单元的最大拉应力和最大压应力总的趋势是不断增加。最大拉应力随着冻结温度降低而减小幅度明显大于最大压应力的减幅。冻结管抗拉强度小于抗压强度,而模拟结果表明其最大拉应力大于最大压应力,因此,在实际井筒冻结基岩段爆破掘进施工过程中,应该将冻结管单元的最大拉应力作为安全控制依据。数值模拟中最大拉应力出现位置存在离散性,为了安全考虑,三个参考位置处的单元的最大拉应力都应该监测。
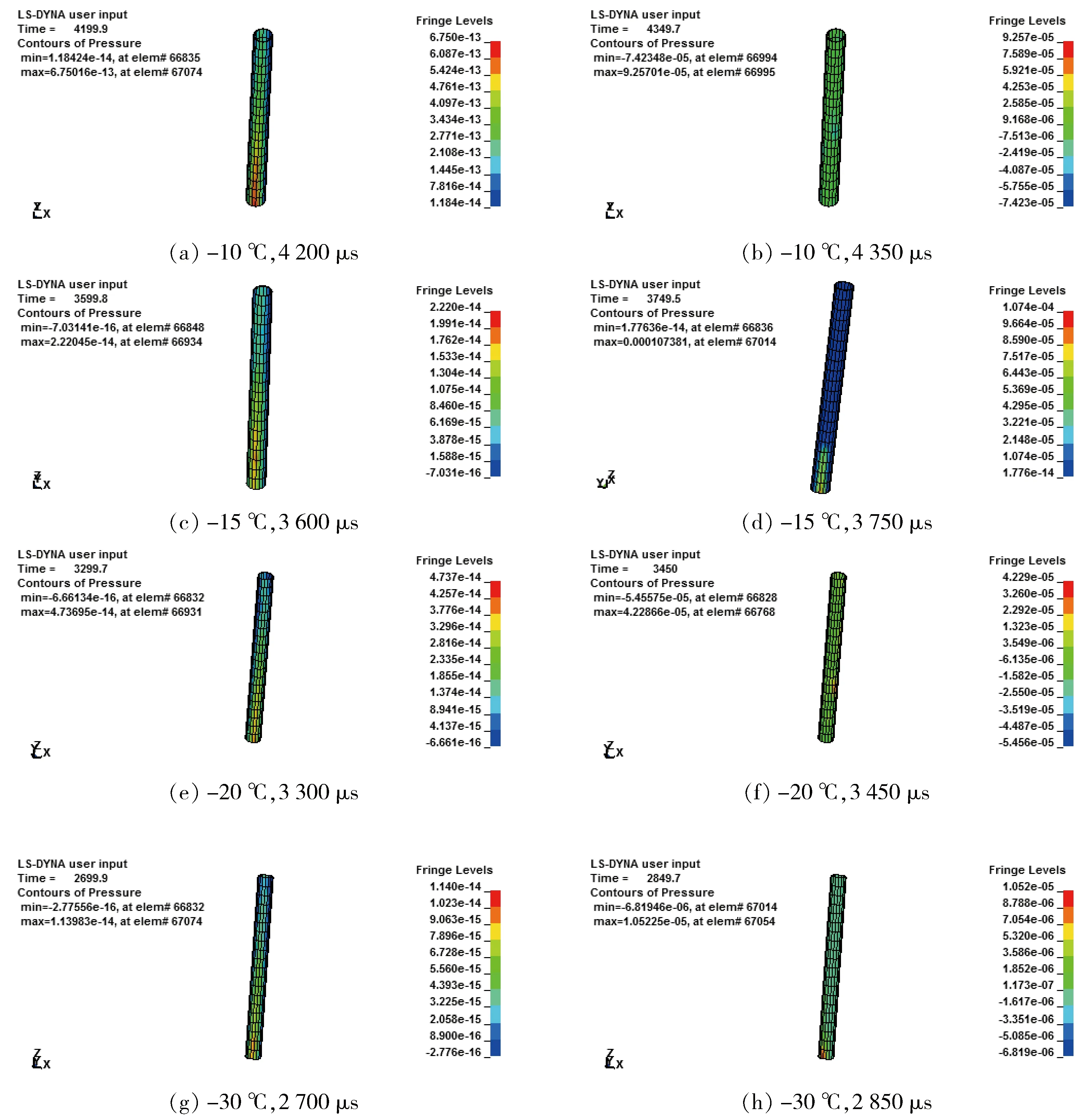
图3 冻结管在不同温度下不同时刻的压力云图
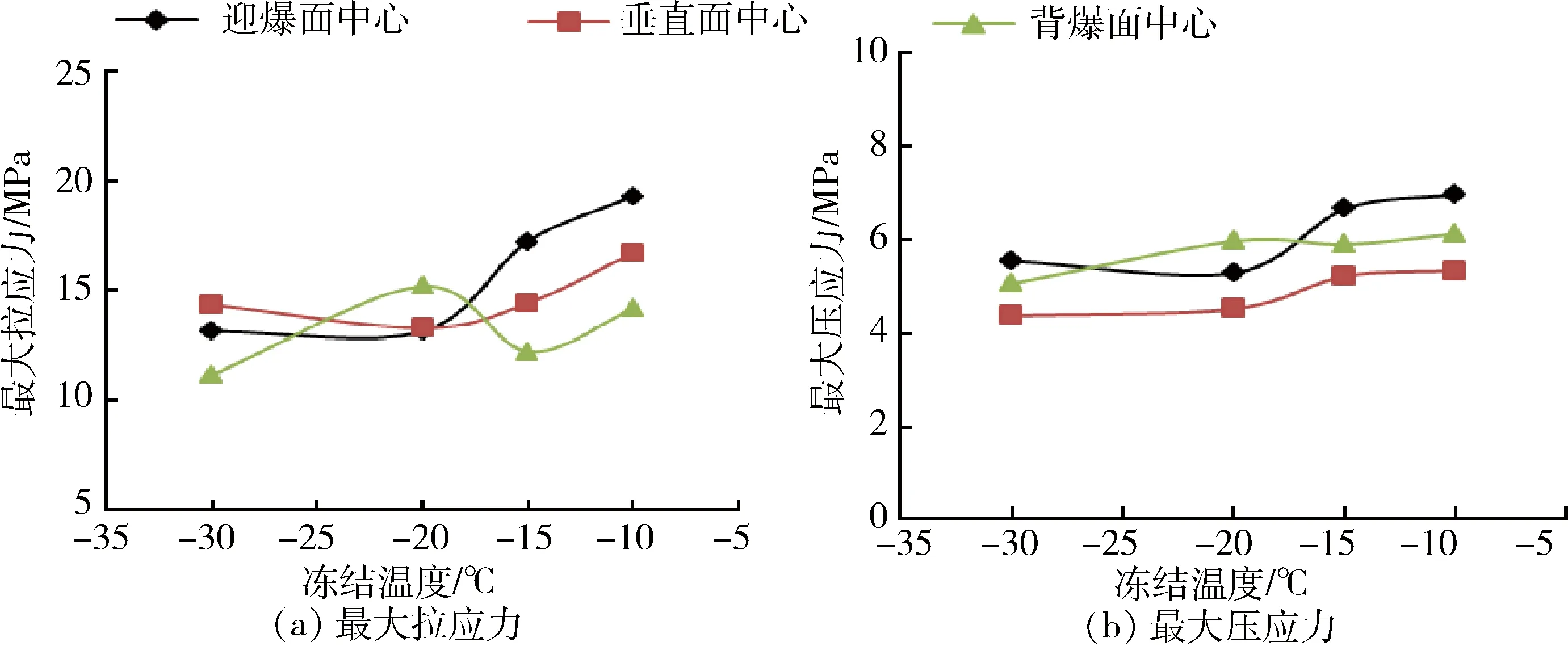
图4 温度-冻结管单元峰值应力关系曲线图
图5为冻结管在不同温度下不同时刻的速度云图。
从图5可以看出,当冻结温度不同时,冻结管出现相似形态规律的速度云图的时间不同。随着冻结温度降低,出现相似形态规律的速度云图的时间不断增长,但是冻结管距离爆源的距离都是相等的,因此温度的变化改变了爆炸应力波在围岩中的传播速度。
将不同冻结温度下不同参考位置处冻结管的径向振动速度和切向振动速度绘成曲线,如图6所示。
从图6可以看出,随着冻结温度的不断降低,总体上冻结管质点振动速度(径向和切向)均是不断减小。温度的不断降低使得负温饱水砂岩的弹性模量和单轴抗压强度不断提高,根据利文斯顿爆破漏斗理论,在炸药性质和药量、炸药位置和深度以及起爆方式等条件一定的情况下,消耗在岩体弹性变形、破裂和破碎、抛掷的炸药爆炸能量越大,则爆炸应力波向远处传播的能量就越低,从而冻结管对爆炸作用的振动响应就越微弱,在质点振动速度上表现为冻结管质点振动速度越低。随着温度的不断降低,冻结管质点振动速度减小的幅度在不断增大,这与冻结岩体的单轴抗压强度和弹性模量增加的幅度在不断增大相呼应。在实际井筒冻结基岩段冻结过程和爆破掘进施工中可以参照本次模拟结果做到冻结管质点振动速度与冻结温度和冻结成本的平衡。质点径向振速要远远大于对应位置处的质点切向振速,因此将质点径向振速作为实际井筒冻结基岩段爆破掘进施工中的安全控制依据。径向振速存在离散性,三个参考位置处的径向振速都应该监测。

图5 冻结管在不同温度下不同时刻的速度云图
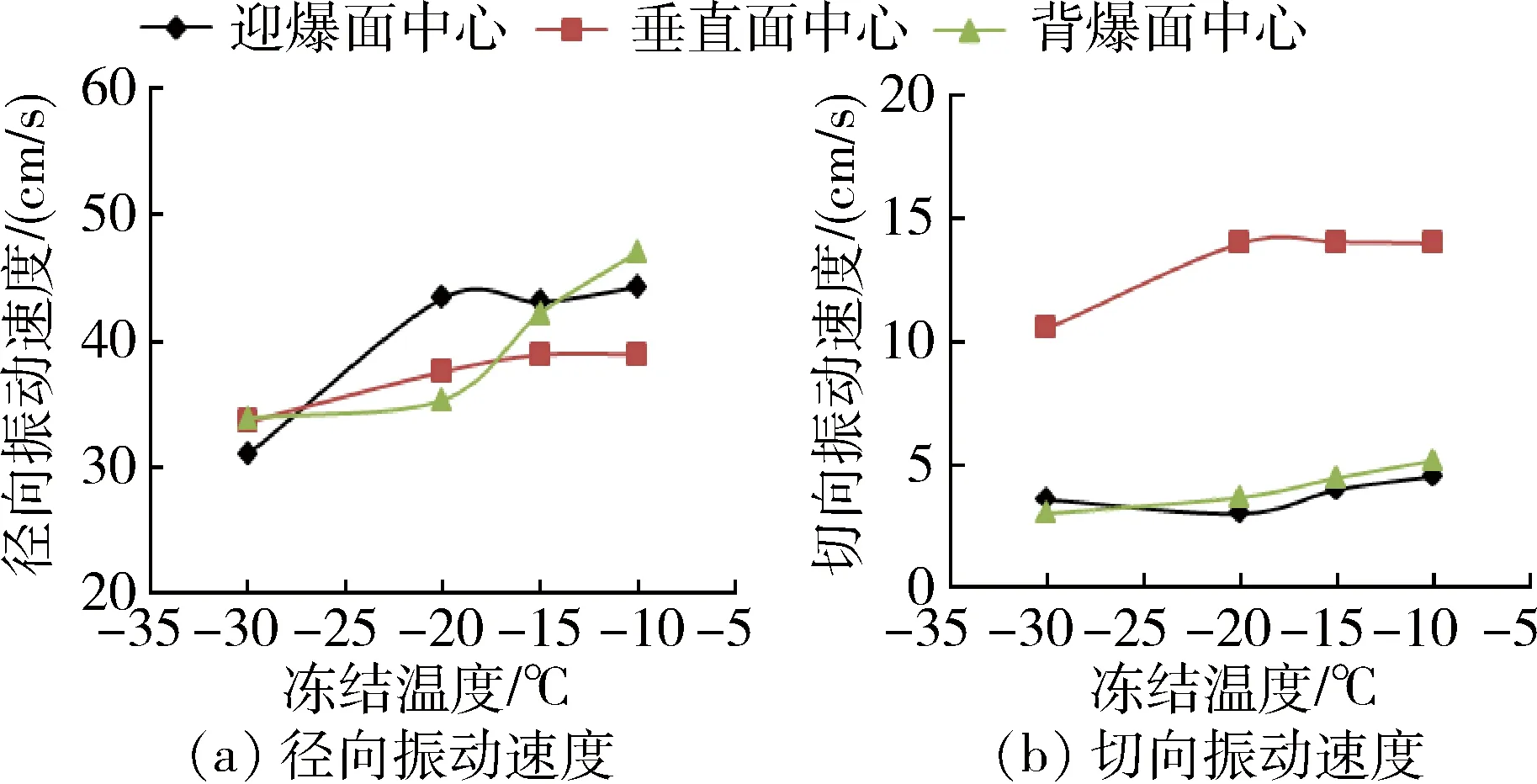
图6 温度-冻结管质点峰值振动速度关系曲线图
4 结 论
1) 运用坐标变换,在复数坐标下,得出爆炸应力波在冻结管周围发生散射时,冻结管的应力场和位移场的复数形式。
2) 随着冻结温度的不断降低,冻结管的最大拉应力、最大压应力、径向振动速度和切向振动速度均是不断降低。
3) 冻结管的最大拉应力大于最大压应力,径向振动速度大于切向振动速度,因此,将冻结管的最大拉应力和径向振动速度作为井筒冻结基岩段爆破掘进施工的安全控制依据。
4) 由于冻结管的最大拉应力和径向振动速度出现位置具有离散性,为了安全起见,在井筒冻结基岩段爆破掘进施工时,三个参考位置都应该作为监测点。
