RSA算法的研究与实现
2018-11-20弋改珍
弋改珍
(咸阳师范学院计算机学院,咸阳 712000)
0 引言
RSA算法是一种迄今为止理论上比较成熟和完善的公钥密码体制,是非对称密码体制的典型代表[1]。在网络、信息安全等许多方面都使用RSA算法,特别是RSA算法典型应用在通信中的数字签名,可实现对手的身份、不可抵赖性验证。在身份认证、信息安全、电子商务中有着广泛的应用前景。
本文介绍了应用于RSA算法中的密码学基础知识,分析了RSA算法的原理与实现步骤,详细分析了RSA实现过程中用到的算法,并在VC环境下,用C++开发语言实现了RSA的加密和解密算法。
1 RSA中的密码学基础知识
密码学实质上体现了数论知识的应用,每一个加密算法体现了不同加密理论,而加密理论又涉及了数论知识。所以,数论知识是加密算法的基础。
定义1(互质关系)[2]:如果两个正整数,除了1以外,没有其他公因子,则称这两个数是互质关系,即互素。
性质1两个正整数互素的性质[3]:
①任意两个质数构成互质关系;
②假设有个质数,后面找到一个数不和前面那个质数成倍数关系,则它们就互质;
③所有的自然数和1都互质;
④p是大于 1的整数,则p-1和p构成互质关系;
⑤p是大于 1的奇数,则p和p-2构成互质关系。
定义2(欧拉函数)[3]:设n为正整数,以φ()n表示不超过n且与n互素的正整数的个数,φ()n称为n的欧拉函数值。
定理1(欧拉定理)[4]:如果a和n两个正整数是互质关系,那么n的欧拉函数φ(n)满足:
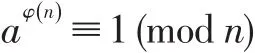
上式说明,a的φ(n)次方除n后的余数是1。
定理2(中国剩余定理)[4]:若a与p1互质,a<p1;b与p2互质,b<p2;c与p1p2互质,c<p1p2。那么,c与数对(a,b)是一一对应关系。由于a的值有φ(p1)种可能,b的值有φ(p2)种可能,那么数对(a,b)有φ(p1)φ(p2)种可能,而c的值有φ(p1p2)种可能。则φ(p1p2)=φ(p1)φ(p2)。
定理3(费马小定理)[4]:若a是正整数,n是质数,质数n满足φ(n)等于p-1,a和n互质,则:
an-1≡1(modn)
定义3(模反元素)[4]:如果两个整数a和n互质,那么一定可找到整数b,使得ab-1被n整除,即:
ab≡1(modn)
2 RSA算法描述
RSA算法由密钥的产生、加密算法和解密算法3个部分组成[1]:
(1)密钥的产生
①产生两个大素数p和q;
②计算n=p×q,欧拉函数φ(n)=(p-1)(q-1)
③选择整数e,使其满足条件:1<e<φ(n),且gcd(e,φ(n) )=1(注:gcd()函数计算两个数的最大公约数);
④计算e的逆元d:d∙e≡1 modφ(n)(注:由于gcd(e,φ(n) )=1,则d一定存在);
⑤取序对(e,n)为公钥,可公开;(d,n)为私钥,对外保密。
(2)加密算法
将要发送的字符串分割为长度为m<n的分组,然后对分组mi执行加密运算,得到密文ci:

(3)解密算法
收到密文ci后,接收者使用自己的私钥执行解密运算,得到明文mi:

3 RSA算法详细设计
3.1 大素数的产生和测试
Miller-Rabin算法是一种基于概率的素数测试方法,在密码学的素数产生中,由于该算法的速度快、原理简单、易于实现,成为进行素数检测的最佳选择[5]。
Miller-Rabin算法[6]是对费马算法改进,它的操作步骤如下:
(1)计算m,满足n=(2r)m+1;
(2)选择随机数a∈[1,n];
(3)若ammodn=1,或满足aimmodn=n-1,则n通过随机数a的测试;
(4)再取不同a要的值对n进行t=5次测试,如果每次测试结果为n是素数,则以高概率判定n是素数。假设n通过t次测试,则判定结果错误的概率是1/4t;若只通过一次测试,素数判定的错误概率是25%。
生成大素数算法的实现流程图,如图1所示。

图1 大素数生成流程图
3.2 密钥e生成模块
通过3.1节的大素数生成模块,可以得到大素数p和大素数q,根据欧拉函数φ(n)=(p-1)(q-1),同时密钥e与φ(n)互质,根据中国剩余定理可以计算密钥e。生成密钥e的算法流程图如图2所示。
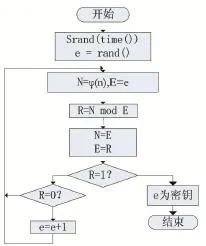
图2 密钥e生成流程图
3.3 密钥d生成模块
通过大素数生成模块得到大素数p和q,密钥e生成模块,根据1=edmod( )p-1(q-1)。利用中国剩余定理计算e的乘法逆元d。
3.4 快速指数算法
得到e后,就可以通过公钥(e,n)进行加密得到密文C。在RSA加密过程中,为了计算ci≡(mi)emodn,采用快速指数算法[7]。将快速指数算法描述为三元组(M,E,Y),其初始值为(M,E,Y)=(mi,e,1)。重复执行以下操作:
①若E是奇数,则Y=M*Ymodn,E=E-1;
②若E是偶数,则X=X*Xmodn,E=E/2。
最终,当E=0时,则Y=X^Emodn。
3.5 RSA加密和解密算法设计
根据2节的RSA算法描述和前面描述的大素数产生算法、密钥e生成算法、求乘法逆元算法、快速指数算法,实现RSA加密/解密算法流程图如图3所示。

图3 RSA算法的流程
4 运行结果与结论
开发环境是VC6.0,使用的语言是VC++,基于对话框应用程序的前提下,完成了RSA算法的加密解密操作,先导入加密密钥,也就是公钥(e,n),然后选择要加密的.txt文本文件,按下生成密文的按钮后,就对文本进行了加密,转化成了另一种不能得知的信息,如4图中生成密文后面文本框的信息是字母和数字的组合。再按下导入解密密钥,即通过(d,n)进行解密。从图4中可以看出密文通过解密恢复了我们能够看得懂的文本信息。

图4 RSA加密系统运行结果图
5 结语
本文研究RSA算法所涉及到的密码学基础概念,在此基础上,分析了RSA算法的基本原理,详细设计了RSA算法实现的各个子模块,并在VC环境下,采用C++语言实现了RSA算法。结果表明,使用加密算法产生的密文,能够被解密算法正确解密。
RSA算法的设计与实现是基于RSA组件的基本算法,随着通信速率不断提高,对加密算法的运行效率也有新的要求。只有有效地改进RSA算法各个组成部分的效率,才能适应通信需求,适应新的网络安全条件。因此,对于RSA算法各组成部分进一步改进,成为今后研究的重要课题。
