改进CUSUM算法的工控系统入侵检测方法

魏战红，王展鹏，王 安，宋玉宝，赵国新

(1.北京石油化工学院 信息工程学院，北京 102617；2.北京化工大学 信息科学与技术学院，北京 100029；3.北京邮电大学 网络与交换技术国家重点实验室信息安全中心，北京 100876)

0 引 言

针对工业控制系统(industrial control system，ICS)面临的信息安全威胁[1-5]，入侵检测系统可以有效监控系统的运行状态，检测入侵行为，为下一步采取安全应对措施，提供依据[6,7]。

入侵检测在ICS环境有如下特殊要求：不能影响ICS本身的可用性、稳定性[8]；实时性高，检测速度快[9]；ICS节点的CPU计算能力往往较弱，检测算法需要简单高效[10]。针对以上要求，CUSUM(cumulative sum)算法检测速度快，计算简便，适用于ICS。CUSUM算法不断改进，李等[11]使用柯尔莫哥夫不等式对CUSUM偏移常数β进行改进。周[12]提出了基于变点CUSUM方法的正态过程方差的CUSUM控制图，在检测大漂移上效率高。张[13]针对非参数CUSUM算法，设计了自适应偏移常数β。但是目前的研究往往不能满足ICS高可用性、高实时性、高检测速度的要求。

本文分析了ICS特点，改进了CUSUM算法，给出了一个基于改进CUSUM算法新的入侵检测方法。该方法首先以传感器获取的实际值和模型的预测值之间的差值为统计序列。然后根据3σ原则设计偏移常数β，并决定门限值τ的取值。最后使用偏差攻击和几何攻击对该入侵检测方法进行实验，验证改进的CUSUM算法能够准确快速地检测出入侵，其误报率较低，适用于ICS环境。

1 ICS入侵模型

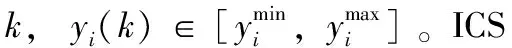
当ICS被攻击时，被攻击的传感器测量信号y′将出现偏差。若y′超过上下限，将检测到异常，触发上下限报警。若y′仍然在上下限范围内，测量值如下

(1)

式中：Ka表示被攻击的时间序列，ai(k)是被攻击时的测量值，其仍在上下限范围内。ICS中被控对象的输入uk决定了输出y(k)。给定被控对象的输入uk，通过下式ICS模型可求得期望输出

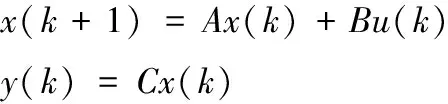
(2)

式中：x(k)=(x1(k),…,xn(k))为k时刻系统输入，y(k)=(y1(k),…ym(k))为k时刻传感器的测量值，矩阵A为状态矩阵，矩阵B输入矩阵，C为输出矩阵。

2 改进CUSUM入侵检测方法

2.1 CUSUM算法

CUSUM算法是一种变化检测方法，它可以检测到统计过程均值的变化。CUSUM算法原理是：如果从某点开始有异常出现，则序列的概率分布会发生改变。整个数列的均值或者方差也发生变化，可判定从该点起为异常。

假设变量x，在无攻击的正常时刻，其统计分布概率为P0，攻击发生后，其统计分布概率为P1。CUSUM算法中N为停止时间，S为累加和。假设S(0)=0，则有

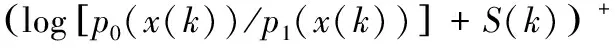
(3)

函数a为

(4)

停止时间N为

N=inf{n:S(n)≥τ}

(5)

式中：inf为下确界，取满足条件的最小值。检测的判定公式

(6)

d(N)用于判断检测序列是否发生变化，τ作为判定入侵的门限值。在n时刻，S(k)>τ，则检测到异常，发出警报。可以看出，CUSUM算法将变化检测问题转化为S(k)和τ的大小比较问题。报警门限值τ决定误报率，τ越小，误报率越高，检测性能越灵敏。

当CUSUM算法用于ICS入侵检测时，存在一定的局限性：由于log[p0(x(k))/p1(x(k))]计算复杂，占用CPU资源较多，很难获得统计分布概率P0、P1。而且ICS中各节点CPU能力较弱，使得检测时间较长，无法满足ICS入侵检测对高实时性的要求。

2.2 改进CUSUM算法

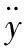
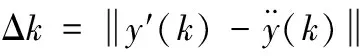
(7)

正常状态下，传感器测量值与预测值几乎相同，差值Δk是一组接近于0的序列；当攻击发生时，Δk将产生较大变化。Δk与log[p0(x(k))/p1(x(k))]有相似的变化，可将log[p0(x(k))/p1(x(k))]简化为差值Δk。

根据CUSUM算法要求，正常状态下，需要S(k)<0；攻击发生后，需要S(k)>0。所以引入一个正值常数β，让大部分Δk-β<0，定义

x(k)=Δk-β

(8)

x(k)作为被检测序列，β是一个比较小的正值常数，使得在正常状态下，期望E(x(k))<0；在攻击发生后，期望E(x(k))>0。累加和S(k)计算如下

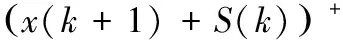
(9)

根据式(4)定义的函数a+，式(9)中累加和S(k)只累计x(k+1)+S(k)为正的值，所以正常状态下，S(k)=0。攻击发生时，Δk变大，x(k)>0，S(k)开始累加。

根据式(6)，当S(k)>τ时，判别函数d(N)=H1，表示系统处于被攻击状态；S(k)≤τ时，d(N)=H0，表示系统处于正常状态。τ越小，约束越严格，检测时间越短，越容易误报。

2.3 参数选取

算法参数β和τ的取值直接影响检测算法的性能。液位控制系统的液位量在正常运行时，预测值Δ和测量值y的差值Δk符合正态分布，则Δk在(μ-3σ,μ+3σ)中的概率为0.9974(μ为期望，σ为标准差)。式(8)中x(k)的期望值需要满足E(x(k))<0，假设β取值为3σ，则x(k)=Δk-β<0的概率为0.9974，期望E(x(k))<0。

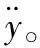
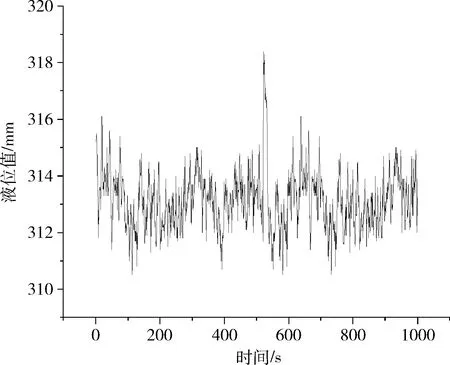
图1 液位测量值分布

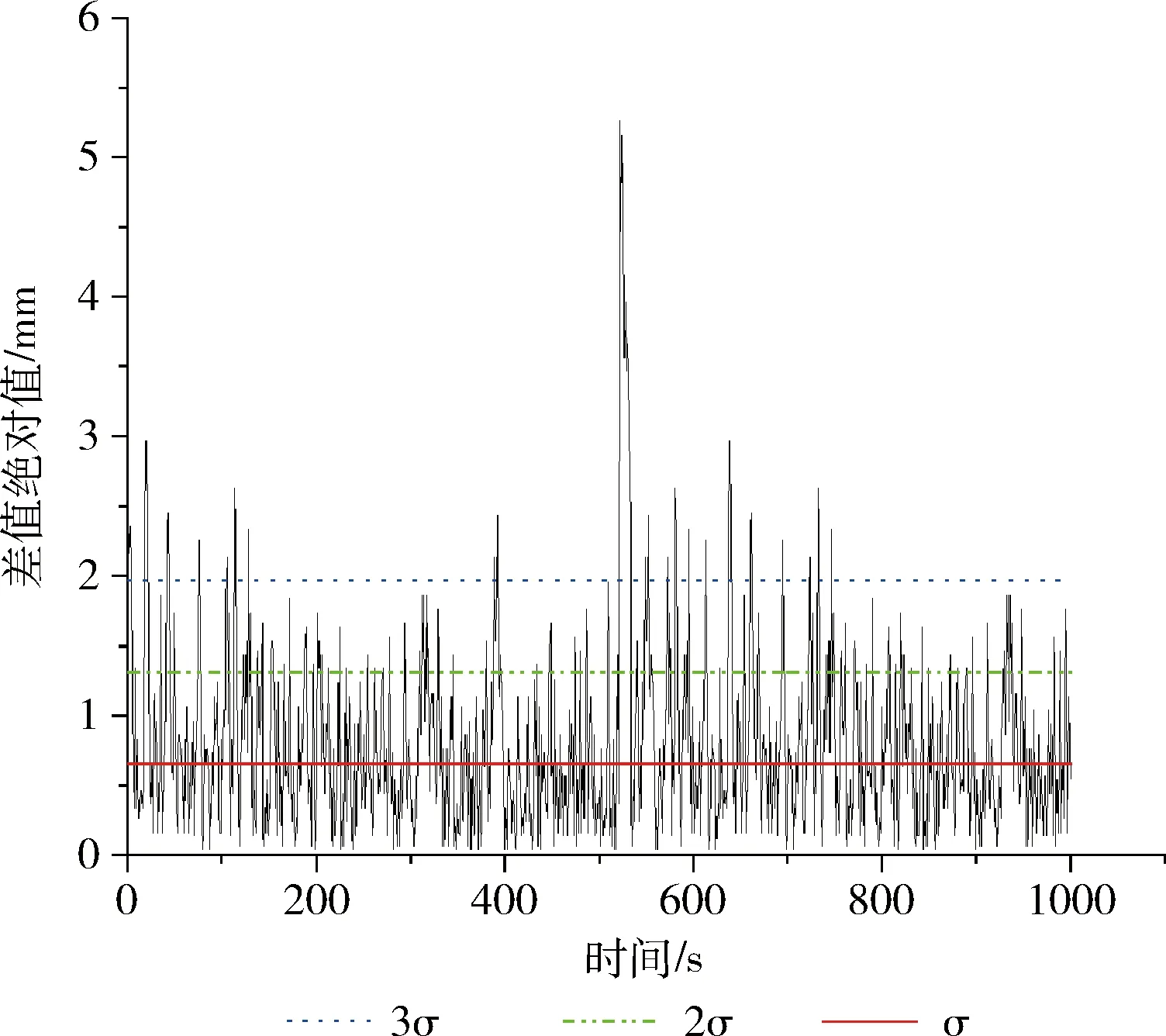
图2 测量值与预测值的差值分布

τ为报警门限值，若S(k)>τ，则检测出异常。τ越小，S(k)越快到达τ报警门限值，检测时间N越短，其误报率越高(液位控制系统的要求液位320 mm以内，在此偏差内报警属于误报)。τ的取值要综合考虑检测时间和误报率。在正常状态下，检测系统根据不同的τ值计算误报率。如图3所示，在τ值为19.8时，误报率为0.1%，理论上取τ值为19.8，即可保持低误报率。

由于S(k)与采样周期有关，如果采样周期很小，即使小偏差也可以使S(k)很大。本系统选用1 s的采样周期，采用比例攻击仿真来选择τ值。τ取值与检测时间关系如图4所示，检测时间随τ变大而变长。τ取值19.8时，检测时间为5 s。对于液位控制系统，5 s的检测时长满足要求。综合考虑了检测时间和误报率后，选取τ值为19.8。

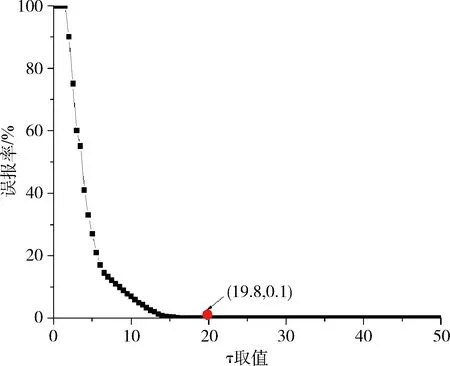
图3 τ取值与误报率关系

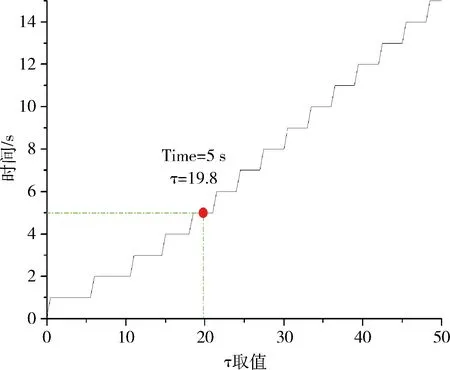
图4 τ取值与检测时间关系

3 方法检验和结果分析

通过模拟攻击者对控制系统攻击，检验改进CUSUM入侵检测方法的性能。攻击目标是液位传感器，使用欺骗手段，对传感器测量值进行修改。

3.1 偏差攻击

偏差攻击是指传感器测量值y(k)被引入了偏差δ(偏差不足以触发上下限报警)，使得控制效果不理想，甚至造成现场危险。液位传感器的正常范围在[0,320]，超过320 mm触发上限报警。加入偏差δ后，液位传感器值为

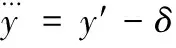
(10)

使用Matlab进行仿真攻击，使用不同δ值，先讨论在上升期的情况下。上升期，罐内进行注水操作，液位不断升高至设定值313 mm。攻击者对液位传感器使用偏差攻击，偏差攻击值δ分别取0、5、30、100，时间范围[0,1200]。偏差攻击下的液位曲线如图5所示，偏差攻击使液位无法到达设定值，设定值和实际值的差值即为δ值。攻击危害出现时刻是液位到达篡改值的时刻(即设定值减去攻击偏差δ值)。攻击下液位与预测液位之间的差值曲线如图6所示，从攻击威胁出现时刻起，差值Δk开始变大，直到Δk=δ。当Δk>β后，S(k)开始累加。在偏差攻击δ值分别取0、5、30、100时，改进CUSUM算法检测时间见表1。当δ=0时，相当于没有攻击，是系统正常状态；当δ=5时，在641 s实际值与预测值产生偏差，偏差攻击开始产生威胁，检测系统在649 s处报警，检测时间为8 s；当δ=30时，检测时间为5 s；当δ=100时，检测时间为2 s。结果表明，在上升期改进CUSUM算法对偏差攻击检测有效，攻击幅度越大，检测越迅速。

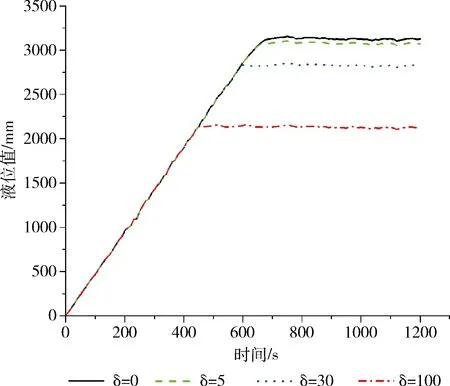
图5 偏差攻击下的液位曲线(上升期)

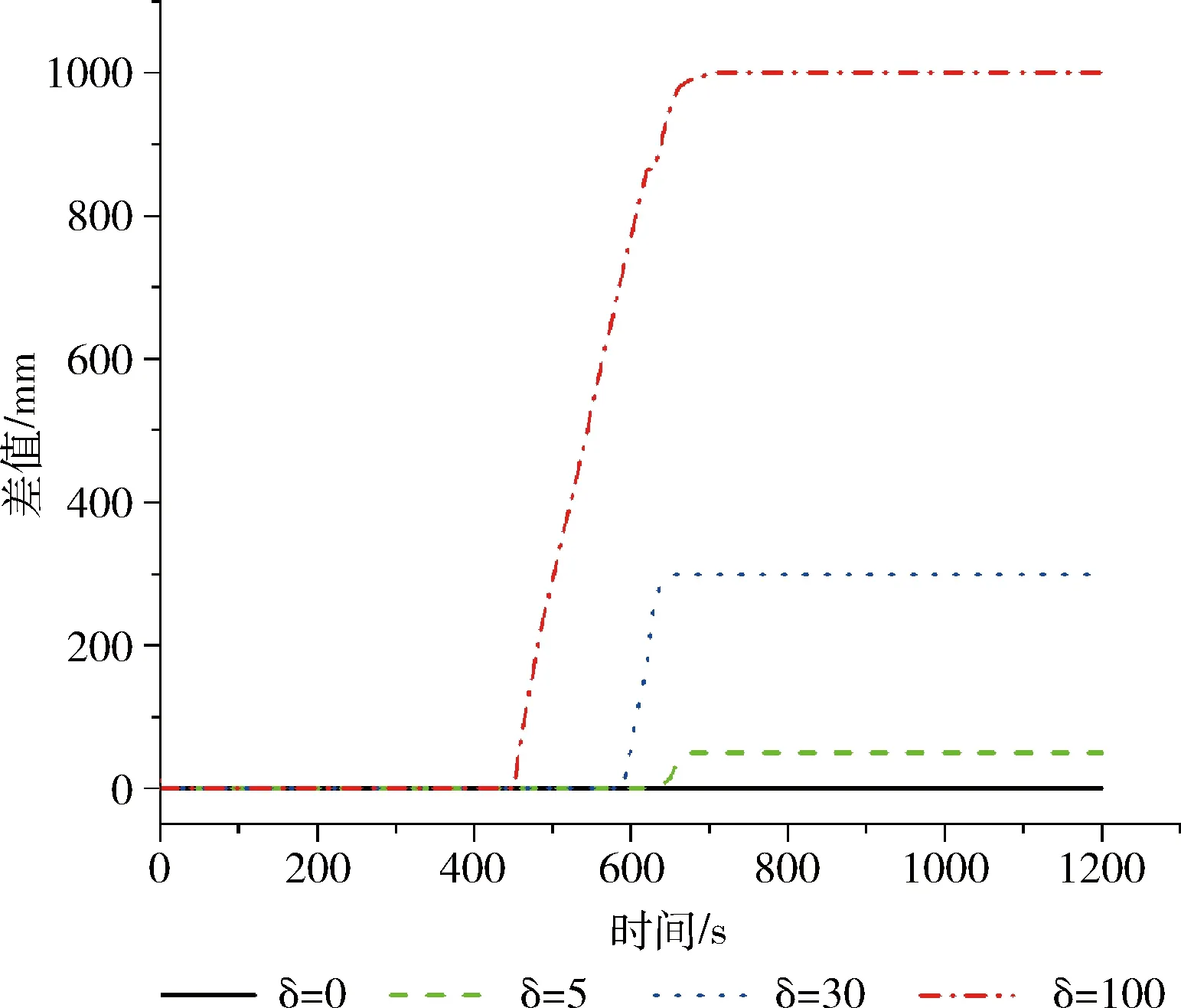
图6 预测值与实际值的差值曲线(上升期)

平稳期，罐内液位保持在313 mm微小波动，在平稳状态下，从800 s开始，攻击者对液位传感器使用偏差攻击δ，δ分别为0、5、30、100。偏差攻击下的液位曲线如图7所示，偏差攻击使液位快速下降，攻击发动便开始产生威胁，液位将偏离原定的设定值。图8表示攻击下实际值与预测值之间的差值曲线，从攻击产生危害开始，Δk迅速变大，直到Δk=δ。改进CUSUM算法检测时间见表2。当δ=0时，相当于没有攻击，是系统正常状态，没有报警；当δ=5时，在800 s实际液位与预测值产生偏差，偏差攻击开始产生危害，检测系统在806 s处报警，检测时间为6 s；当δ=30时，检测时间为3 s；当δ=100时，检测时间为2 s。结果表明，在平稳期改进CUSUM算法对偏差攻击检测有效，检测速度快。

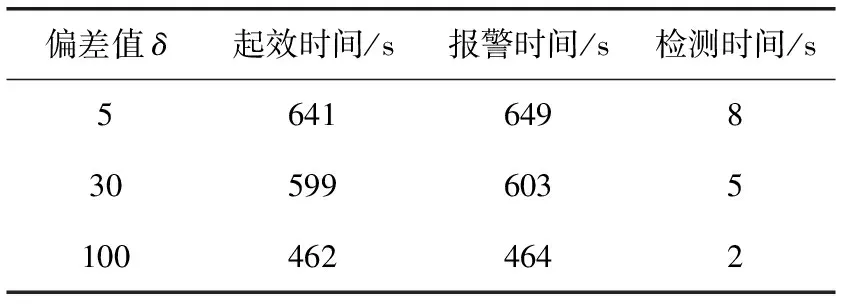
表1 偏差攻击下的报警时间(上升期)

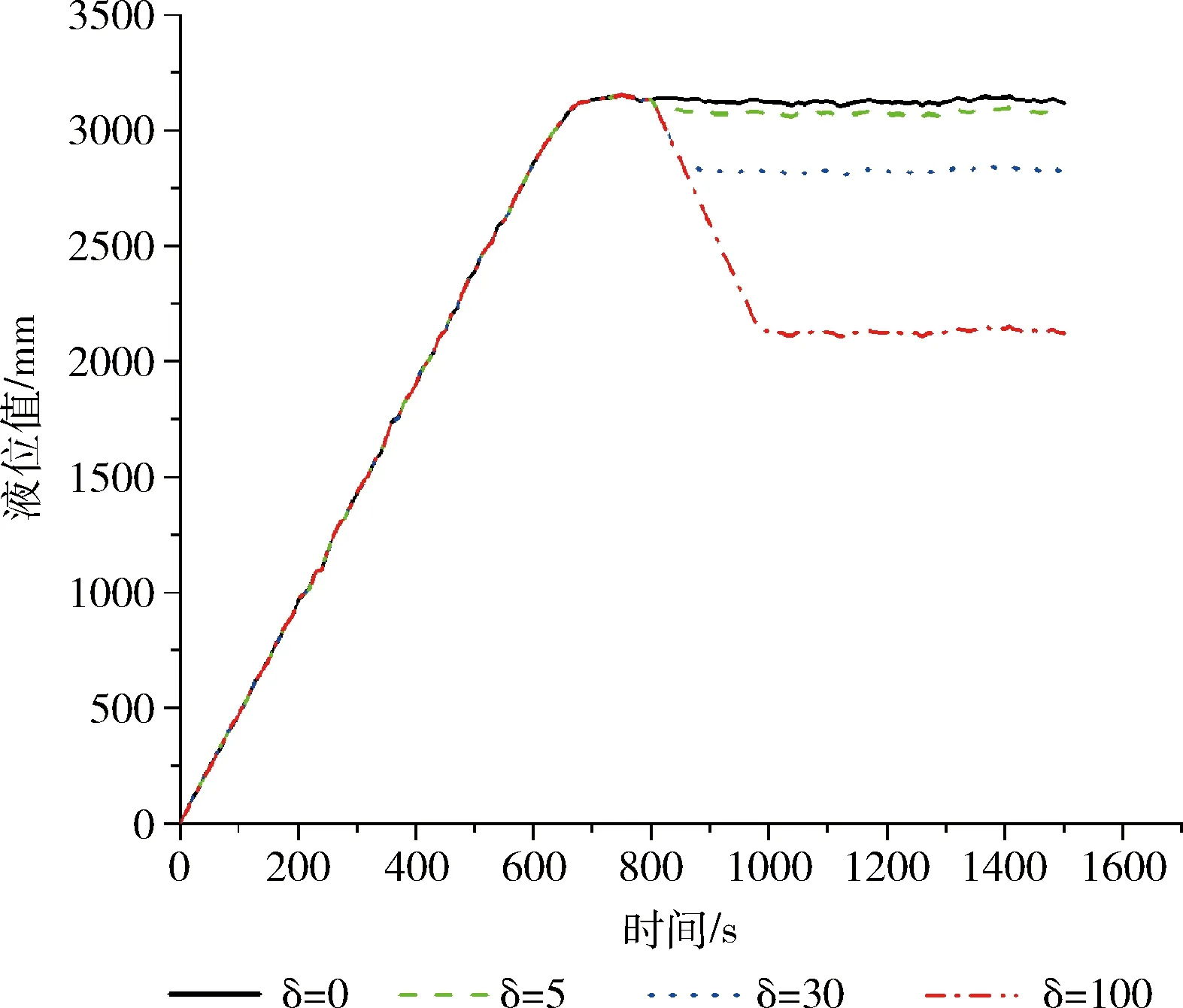
图7 攻击下的液位曲线(平稳期)

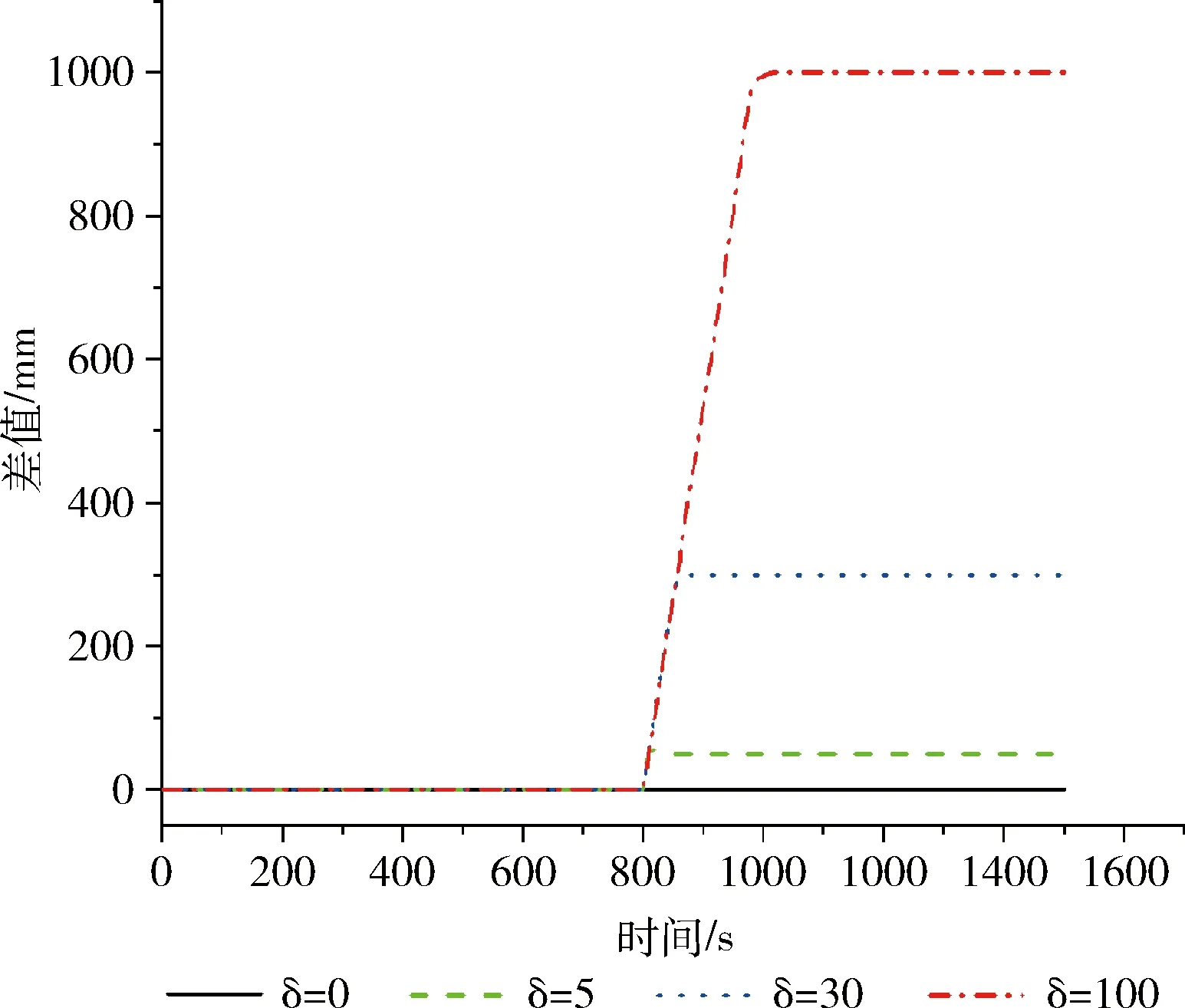
图8 预测值与实际值的差值曲线(平稳期)

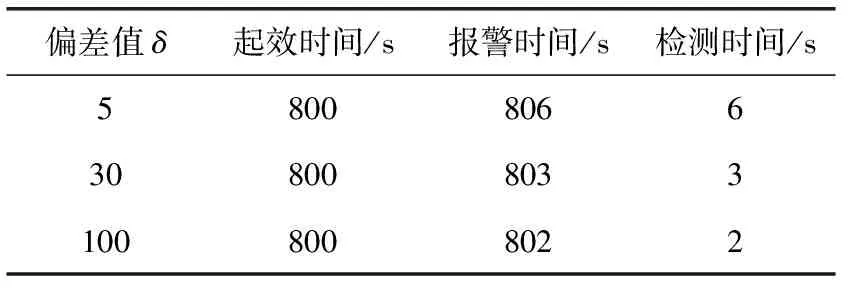
表2 偏差攻击下的报警时间(平稳期)

3.2 几何攻击

几何攻击具有初始变化缓慢不易侦查，一段时间后几何式爆发的特点，对工业控制系统造成巨大影响。几何攻击可以表示为

(11)

nk时，攻击呈几何式增长。选定参数η=1.8,γ=0.75,k=10。几何攻击下的液位如图9所示。

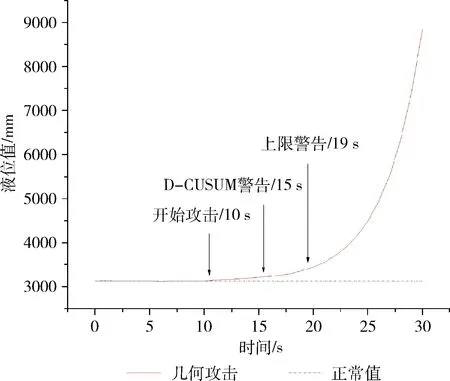
图9 几何攻击下液位实际值分布

攻击从10 s开始产生威胁，改进CUSUM在15 s报警，检测时间为5 s；液位上限报警在19 s触发，历时9 s。在几何攻击下改进CUSUM算法5 s便能快速做出反应，检测速度较快。

4 结束语

工业控制系统的入侵检测有高可用性、高实时性的要求。针对工业控制系统的特点，提出了一种基于改进CUSUM算法的ICS入侵检测方法。该方法以模型预测值与实际测量值之间的差值作为检测序列，根据3σ原则设计偏移常数β，并决定门限值τ的取值。通过偏差攻击和几何攻击实验，检验改进CUSUM入侵检测方法性能。实验结果表明，改进CUSUM入侵检测方法检测时间较短，误报率低，检测率高，在工业控制系统入侵检测中有实际应用价值。由于β参数和门限值τ与误报率、检测时间、检测率相互关联，进一步优化对参数的选取，是接下来的研究方向。