基于引力搜索和分数阶理论的高效路由算法
2018-11-17肖志良
肖志良
(1.佛山职业技术学院 电子信息学院,广东 佛山 528137;2.武汉大学 信息管理学院,湖北 武汉 430072)
0 引 言
当前,IoT[1,2]被视为在传感器、执行器、手机等网络对象之间进行交互的无线传感器网络(wireless sensor networks,WSN)新范式[3,4]。其最大难题之一是如何提高节点的能量和工作寿命[5]。因此,一个高效的路由协议至关重要。在众多路由协议中,有3类不同方法被广泛用于节点聚类,即基于划分聚类、基于优化的聚类和基于LEACH的聚类。
基于划分聚类有代表性的如文献[6],提出了CRT2FLACO聚类协议,该模型以蚁群优化[7](ant colony optimization,ACO)能量均衡为基础。根据经验选择设计规则。基于优化的聚类使用较多,如Sun等[8]提出了用于WSN基于优化的路由协议,即进化算法的分簇路由协议(evolutionary routing-clustering protocol,ERP)。Lei等[9]提出了多粒子群免疫协同算法(MPSICA),以实现智能化路由恢复方案。基于LEACH的聚类也得到了广泛应用,如Chen等[10]提出了一个基于聚类的协议,即LEACH改进的多跳路由协议,以局部簇或簇头的基站(base station,BS)的随机旋转在传感器节点间实现能量负载的均匀分布。Singh等[11]提出了带低能量自适应聚类分层的多跳路由协议(MR-LEACH)。为延长WSN的工作寿命,MRLEACH将网络分割为许多不同的聚类层。
本文主要目的是设计并开发出一个用于IoT的路由协议,即分数阶理论-引力搜索(fractional theory-gravitational search algorithm,FT-GSA)路由算法,其主要工作是将分数阶理论纳入引力搜索算法中,以确定最优簇头。利用链路工作寿命、延迟、能量和距离来延长节点的工作寿命。
1 物联网网络模型
IoT网络包括无线传感器网络(WSN)以及其它连接到互联网的各种设备。基于无线传感器网络的IoT体系结构如图1所示。

图1 基于WSN的IoT网络的体系结构
如图1,基于WSN的IoT网络包括一个基站或汇聚节点DB,簇头HC,以及h个IoT节点。IoT节点之间的无线链路表示射频通信范围内的直接通信。每个IoT节点均有一个唯一ID,且这些节点以分组的形式在网络中形成聚类。节点使用簇头机制将数据包传输到基站或汇聚节点。
2 提出的算法
本文目的是设计开发出用于IoT网络的高效路由协议。所提方法的原理图如图2所示。提出的IoT网络模型包括一个基站和多个IoT节点。通过一个高效路由进行数据包传输,以延长IoT节点的工作寿命。本文将链路工作寿命、节点的累积能量水平、节点之间的延迟扩展和距离等多个目标用于表述新的适应度函数。然后,在FT-GSA算法内嵌入这些多目标函数,从而为使用IoT节点进行能量高效的路由选择最优簇头节点。
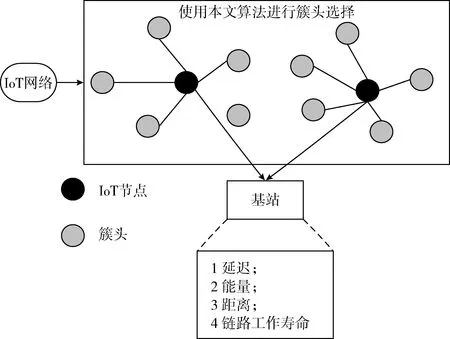
图2 本文方法的原理
FT-GSA算法将应用于PSO的分数阶理论[12]合并到GSA[13]算法中,根据时间对节点主体位置进行更新,由此,通过GSA中的数学公式,基于分数导数生成新的解。利用选出的簇头节点将数据包传输至基站,以在IoT网络中实现能量高效的路由,从而增加了网络的工作寿命。下面对算法进行简要描述。
2.1 初始化

2.2 力与加速度
“力”表示在时间e处两个节点主体之间所产生的力。由此,节点主体j在特定的时间e处作用在节点主体i上的力可以表示为
(1)


(2)
作用在聚类r中的节点主体i上的合力为网络中其它节点主体施加在第r个组件上的力的随机加权和
(3)


(4)
式中:mii为节点主体i的惯性质量。节点主体在下一个时间处的速度为其当前速度的一部分与其加速度的和。因此,节点主体i的速度可表示为
(5)

2.3 分数阶理论
若节点主体包含较重的质量,则由于其在搜索空间移动较慢,会造成性能下降,从而产生开发问题。由于邻近节点的更新特性,GSA算法中会出现探索问题。本文将分数阶理论与GSA算法进行合并,以求解开发和探索问题。分数阶微积分主要被用于降低实施难度,并在分数阶导数方面提供更好的更新行为。为进一步迭代,使用分数阶理论对节点主体的位置进行更新
(6)
(7)
(8)
离散导数的阶可被泛化为一个实数0≤α≤1。因此,上述公式可表示为
(9)
(10)
2.4 适应度函数
在FT-GSA算法中通过适应度函数求出引力质量和惯性质量。所提算法在适应度函数中使用了4个参数,即距离、能量、延迟和链路寿命。若节点主体被考虑为簇头,则聚类成员与该簇头之间的距离较短。由此,将网络的工作寿命最大化的适应度函数表示为

(11)
其中,α、β、δ和η为加权参数,这些加权值总和为1。下面对式(11)的4个加权参数进行简单说明。第1个参数属于节点之间距离的目标函数,为了实现网络整体寿命的最大化,其值非常小;第2个参数属于适应度评价中能量方面的目标函数,为了最大化网络工作寿命,该参数应该始终较高;第3个参数用于评估延迟,以进行簇头选择。延迟与聚类中成员数量成正比。为了最大化网络寿命,延迟应该较低;第4个参数为链路寿命,在对链路寿命[14](link life time,LLT)进行预测时考虑了多个参数。每个聚类中,链路存在于每个IoT节点与其对应的簇头节点之间。LLT为每个聚类提供数据传输的最大持续时间。链路寿命的数值越高,网络工作寿命越大。
2.5 最优解
通过分数阶理论对节点主体的位置进行更新后,使用节点主体i的适应度数值更新用于下一个迭代的质量
(12)

2.6 终 止
使用适应度函数,可以对节点主体的适应度数值进行评估。其后,重复对节点主体位置进行更新,直到选出最优簇头。所提FT-GSA算法的伪代码如下。即:通过节点之间评估出的最短路径(单路径或多路径)进行数据传输,以延长节点的工作寿命。
3 仿真结果与分析
3.1 仿真设置
IoT网络和所提FT-GSA算法使用的固定参数数值见表1。FT-GSA算法的时间复杂度主要分为两部分:贪婪算法找出主体位置的时间O(N·log2N)、分数阶理论与GSA算法合并搜素的时间O(N·Tm·MaxC),其中N为总节点数量,MaxC是最大迭代数量,Tm为迭代一次所需时间。其总体复杂度为:O(N·log2N+N·Tm·MaxC)。

表1 用于仿真实验的固定参数值
3.2 仿真结果
所提FT-GSA算法的仿真结果如图3所示。包括100个IoT节点,通过4个不同的轮数给出相对于基站的节点位置。图3(a)是第一轮节点的初始位置。深黑色节点表示IoT节点,灰色节点则表示簇头。初始时,所有节点的能量均相同(假定为1)。其后,使用提出的方法在第一轮中进行簇头选择。该算法基于距离、能量、延迟、链路寿命4个因素选择簇头。在整个通信过程中对每个节点的能量进行更新。图3(b)是500轮后的节点位置示意图。图3(c)表示1500轮后节点位置示意图。最小的黑色节点表示死亡节点,此处死亡节点被用于终止节点之间的数据传输。图3(d)给出了2000轮后的死亡节点和簇头节点的示意图。从中看出,即使在最大轮数下,提出的FT-GSA算法依然能够保持至少一个存活节点,由此验证了本文算法的有效性。

图3 仿真结果
3.3 仿真结果
本文通过存活节点和网络能量估计出能够提高网络寿命的加权常数。对照组有:与多粒子群免疫协同算法[9](MPSICA)和带低能量自适应聚类分层的多跳路由协议[11](MR-LEACH)。
3.3.1 基于存活节点的性能比较
各算法的性能比较如图4所示。图4(a)给出了IoT节点数量为100时的性能比较。在第1100轮,MPSICA和MR-LEACH的存活节点数量分别为17和74。而本文FT-GSA算法的存活节点数量则为100个。而在第2000轮,所提FT-GSA算法依然有7个存活节点,高于其它算法。图4(b)给出了在200个IoT节点的场景性能比较。提出的FT-GSA算法在800轮得到200个存活节点,随后逐渐降低。在最大轮数即第2000轮,提出的方法得到了21个存活节点。相比于其它方法,得到更多的存活节点。由此验证所提方法能够增加网络的工作寿命。这主要是因为本文方法综合考虑了能量、距离、链路寿命和延迟等多个目标。通过修改适应度函数,聚类成员与该簇头之间的距离较短。网络的工作寿命得到了最大化。而MPSICA算法通过睡眠机制对网络的能耗控制进行调整。其控制参数较多,随着轮数增加,难以控制工作时长。MR-LEACH主要缺点是聚类层级必须在能量消耗最小的层次内定义,这造成了聚类成员与簇头变长,存活的节点数在轮数不高的情况下就达到了最低值。

图4 利用存活节点数量进行性能比较
3.3.2 基于网络能量的性能比较
各算法在网络能量方面的比较如图5所示。图5(a)给出了100个IoT节点场景下的网络能量分析。当使用750轮进行簇头选择时,MPSICA和MR-LEACH的能量值分别为0.1439和0.2238,而本文算法则实现了0.3055的能量数值。与MPSICA和MR-LEACH相比,本文FT-GSA算法在所有轮数中的能量数值均明显较高。图5(b)给出了在200个IoT节点的场景下,轮数与归一化网络能量之间的权衡关系,其中归一化网络能量是网络能量的另一种表示形式,也是一种规整化处理,即当前能量在最大和最小能量间距中所占的比例。MPSICA算法在第一轮实现了0.5496的能量值,随后逐渐下降至0.0263。所提算法则在初始时得到0.5497的能量值。当轮数增加到2000时该能量值降低为0.0403。由此可以做出结论,与MPSICA和MR-LEACH算法相比,所提算法在所有轮数中均得到了最大的网络能量。这主要是因为本文方法将能量因素嵌入到适应度函数中。将分数阶理论纳入引力搜索算法中,使得路径搜索加快,快速确定最优簇头,网络能量最优。
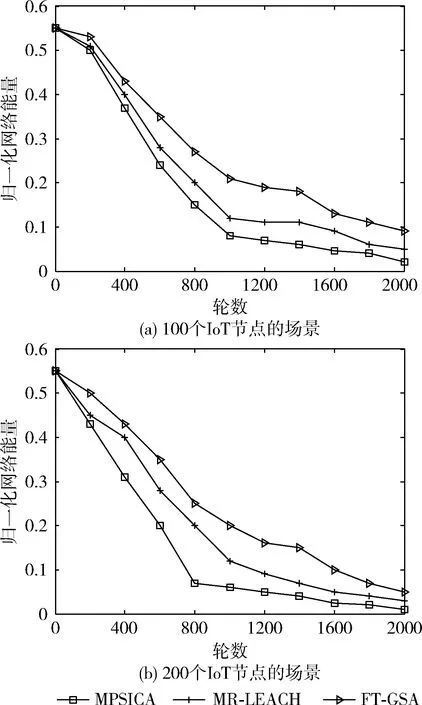
图5 基于网络能量的性能比较
执行2000轮后的数值比较结果见表2。对于100个节点的场景,MPSICA和MR-LEACH方法得到的结果分别为0.58和0.63。而本文FT-GSA方法得出的延迟最低,数值为0.51。当节点数量为200时,所提方法的链路寿命为0.049,而MPSICA和MR-LEACH得出的数值分别为0.035和0.039。在网络能量分析中,所提FT-GSA算法在第2000轮的最低能量为0.040。由表2可知,本文FT-GSA算法在多个度量中均表现出优于现有其它方法的性能。
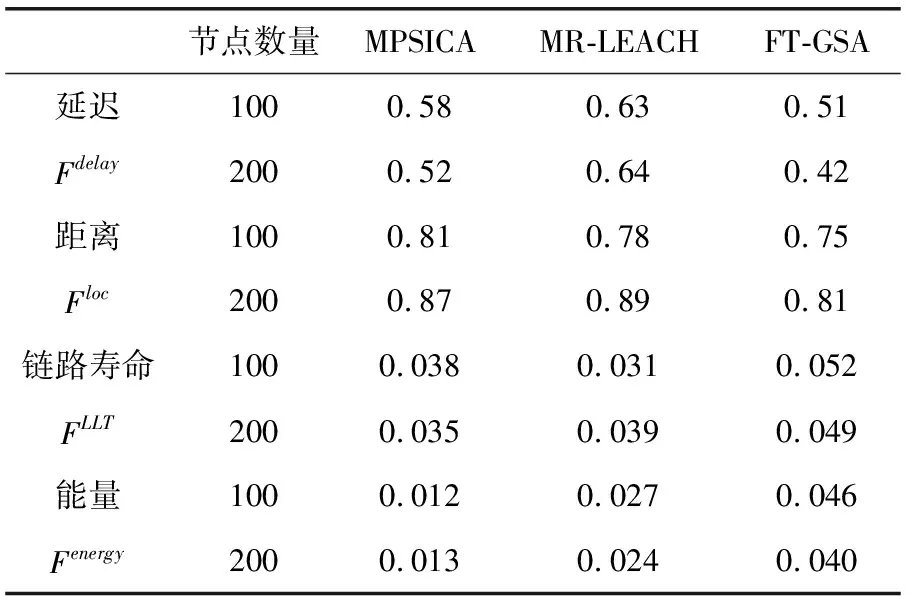
表2 2000轮后各算法的性能比较
4 结束语
本文对每个IoT节点的能量进行估计,以通过有效路由进行数据包传输。所提算法结合了分数阶理论和引力搜索算法,以迭代的方式确定簇头,使用了4个目标函数,即距离、延迟、链路寿命和能量。通过存活节点数量和网络能量的分析说明了本文算法可以增加存活节点的数量和网络能量,从而能够延长节点的工作寿命。未来将对IoT网络参数在实际应用中的效果,以及FT-GSA算法中4个参数的设定对网络能量的影响进行分析和研究。另外,IoT在移动端的应用也将是重要研究内容。
