巧借花容添月色——极化恒等式在数量积问题中的应用赏析

☉江 苏 省 常 熟 中 学 章文昊

☉江苏省常熟市浒浦高级中学 殷伟康

一、极化恒等式概念的解读

上式表明向量的数量积可以由向量和、差运算的模来表示，该式沟通了向量的数量积与向量线性运算的关系，将不可度量的向量的数量积关系转化为可度量、可计算的数量关系.

图1

极化恒等式的几何意义：如图1，在△ABC中，D是BC的中点，则向量的数量积可转化为中线长与半底边长的平方差，揭示了三角形中线与边的关系，也可以理解为向量的数量积可表示为以这组向量为邻边的平行四边形的“和对角线”与“差对角线”平方差的.形象地通过几何图形将向量的数量积进行合理展示，促进学生对数量积概念的理解.极化恒等式最明显的特征是两个向量必须共起点，点D是两个向量夹角所对第三向量（这两个向量之差）上的中点.极化恒等式将向量的数量积转化为两个向量模的关系，从而建立起了向量与几何长度（数量）之间的关联，实现了向量与几何、代数三者的有机结合，有利于培养学生的直观想象和数学建模素养.

二、极化恒等式的应用赏析

在求解向量的数量积问题时，常用方法是基底法、坐标法和图形法（几何意义法），但有时其解题过程由于运算复杂、过程繁冗而导致错误.若能巧用极化恒等式，往往化繁为简，快速找到解题突破口.本文以近几年高考、江苏省大市级统考试题为例，对极化恒等式在数量积问题中的应用进行归类剖析，探索其解题规律，并赏析其独特的解题魅力.

（一）用极化恒等式巧求数量积的值

例1（2016年江苏卷）如图2，在△ABC中，D是BC的中点，E，F是AD上的两个三等分点，的值是______.

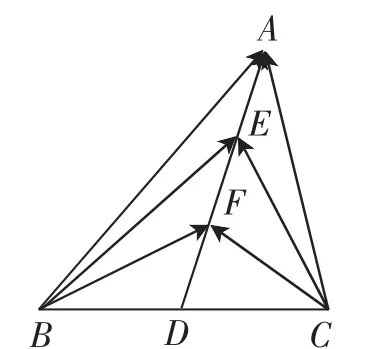
图2

评注：解决平面向量问题的通性通法是选好一组不共线的基底向量，并运用它们表示其他向量.本题的解题关键是把已知条件与所求目标转化为运用来表示.平面向量数量积问题的另一种解法就是建立平面直角坐标系，把数量积转化为坐标的运算.运用向量的性质可以将分别转化为共起点的向量数量积，利用极化恒等式构造方程组，从而求出的值. 对于从中线与底边这两个方向寻找基底向量的数量积问题，可以运用极化恒等式，把数量积转化为数量的运算，这样能更快地寻找到解题思路.

例2 （2018年苏北四市高三第一学期期末试题）如图3，在△ABC中，已知AB=3，AC=2，∠BAC=120°，D为边BC的中点.若CE⊥AD，垂足为E，则的值为______.

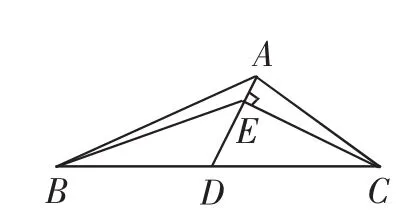
图3

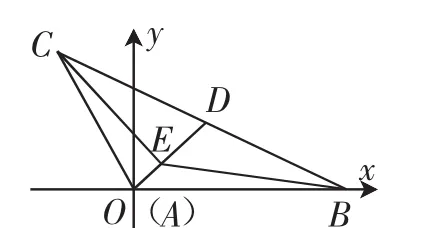
图4

解法1（坐标法）：如图4，以A为原点，AB所在直线为x轴，建立平面直角坐标系，则

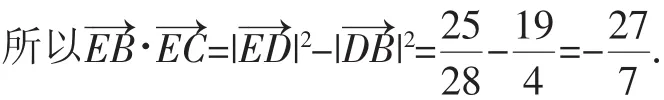
评注：不少同学试图从基底法角度进行探求，结果无功而返.尝试坐标法，却又不知如何合理建立坐标系.解法1是根据图形的特征，变换角度，重新设置图形（便于三角形的顶点用坐标表示），如图4，以A为原点，AB所在直线为x轴，建立坐标系，将向量数量积问题转化为代数问题来求解.代数与几何二者的有效结合，可以最大程度上优化解题过程，提高解题效率.解法2是利用余弦定理先计算出BC长度，运用极化恒等式求出|，再利用面积关系求得||， 然后利用向量知识将转化为仅含|的关系式即可.解法3是在解法2基础上的改进，利用△ACD的三条边及余弦定理计算出cos∠ADC值，利用Rt△DCE的边角关系求出||，再运用极化恒等式将即可.

（二）用极化恒等式探求数量积的最值

例3（2012年南京市二模）在面积为2的△ABC中，E，F分别是AB，AC的中点，点P在直线EF上，则—的最小值是______.

解法1（坐标法）：由题设知，△PBC的面积为1，以B为原点，BC所在直线为x轴，过点B与直线BC垂直的直线为y轴建立平面直角坐标系，设

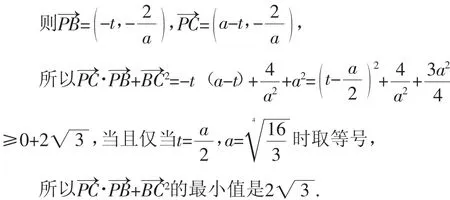
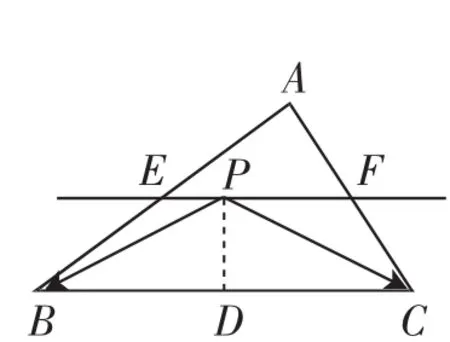
图5

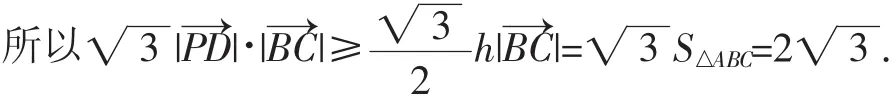
变式 在面积为2的△ABC中，E，F分别是AB，AC的中点，点P是直线EF上的任意一点，则的最小值是______.

解析：如图5，取BC中点D，

评注：对例3及其变式的解题方法进行反思：能否找到这类问题的本质？这类问题隐含的数学背景是什么？这类问题能否进行推广？目标问题—实质上是外森比克不等式的另一种表示形式.外森比克不等式是经典数学模型，已知a，b，c是△ABC的三条边长，△ABC的面积为S，则a2+b2+c2≥4S.运用极化恒等式对例3变式进行如下推广.

推广1：在面积为2S的△ABC中，E，F分别是AB，AC的中点，点P是直线EF上的任意一点，则—的最小值是

推广2：在面积为2S的△ABC中，E，F分别是AB，AC的中点，点P是直线EF上的任意一点，则的最小值是

推广3：在面积为2S的△ABC中，E，F分别是AB，AC的中点，点P是直线EF上的任意一点，当-2≤λ≤2，则

通过问题的系列变式和推广，层层递进，探究数学规律，体验数学研究过程，领悟问题本质，把握方法要领，促进思维能力提升，并能从中领略与欣赏极化恒等式之妙用，培育数学抽象和数学模型等数学素养.

（三）用极化恒等式确定数量积的取值范围

例4（2015年南通市三模）如图6，已知正方形ABCD的边长为2，点E为AB的中点.以A为圆心，AE为半径，作弧交AD于点F.若P为劣弧E（F上的动点，则P—的取值范围是______.

解析：如图6，取CD中点M，

由极化恒等式得

图6

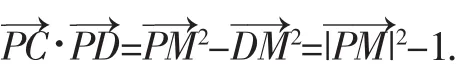
向量数量积问题具有综合性强、灵活性大等特点，其难点是解题方向不明确，因而解题方法和解题工具的合理选择显得尤为重要.极化恒等式不仅是一种基向量思想的公式化表达式，而且在解决向量数量积问题中有着不可估量的作用.在欣赏极化恒等式妙用过程中，体会到极化恒等式也是破解向量数量积问题的利器之一.因而在解决掌握向量数量积最值、取值范围问题通性通法（基底法、坐标法、几何意义法）的基础上，若能根据图形特征，巧妙地运用极化恒等式进行思考与探求，实现数形思维的转换，有利于拓宽解题思路和方法，提升直观想象、逻辑推理、数学模型和数学运算等数学核心素养.