“问渠”在何处，“源头”教材中——对回归教材的思考及做法

☉安徽省无为中学 方 兴

在高三复习阶段，有一个必不可少的环节就是回归教材.对于回归教材，或许有的教师不够重视，不以为然，或许有的教师流于形式，没有真正落到实处.个人以为，在高三整个复习阶段，提升对回归教材的重视程度、实施回归教材的科学做法，把回归教材真正落实到位是很有必要的，这也是科学备考、让学生在高考中取得理想成绩的关键所在.下面谈一谈个人对回归教材的理解和自己的一些尚不成熟的做法.

离开了教材就离开了高考，离开了教材容易导致失去方向，形成低效.如何回归教材，利用好教材，这个问题看似简单，实则复杂.值得老师们研究.本人回归教材的做法分三个层次.

一、“看山是山”——原汁原味回归教材

1.“阅读”+“三会”

要求学生带着思考、针对自己的薄弱点、易错点认真阅读教材，做到准确和实质性理解基本概念，熟记重要公式、定理，回顾概念的形成过程，熟知教材中的定理、公式的推导方法，“三会”是指学生对课本上的例习题要会做，定理要会证，公式要会推导.特别一提的是：必修1～必修5，选修2-1～选修2-3共有28个阅读与思考栏目，15个探究和发现栏目，13个信息技术栏目，对教材上的这些内容也不可忽视，这部分内容是所学知识的延伸和拓展，往往受到命题者的青睐，对主要章节内容要求学生画知识结构图.

学生通过阅读教材，力求做到：知识内容梳理无遗漏，基本方法熟知无盲点，基本题型概括要全面.

2.“整理”+“辅练”

教师在研究《考试大纲》和说明的基础上，对考纲规定的200多个知识点进行详细整理，根据三个层次（了解、理解、掌握）的要求对知识点进行归类，再结合研究近几年的高考真题，列出高频考点.这样的过程既是让知识系统化的过程，也是去粗取精、进一步让高考所考的知识点更加清晰凸显出来的过程，使得学生查缺补漏更加有针对性，从而提高复习的有效性.当然，仅仅对知识点归纳和梳理是不够的，还必须辅以针对性的习题，帮助学生厘清易错点，强化学生对概念准确、实质性理解，熟练掌握公式定理的应用.

二、“看山不是山”——对教材内容“再创造”式回归教材

如果我们仅仅从知识点层面上回归教材，那是“只见树木，不见森林”，是“只见其表，不知其里”，那么必然使得回归教材的效果大打折扣，从而导致复习的低效.在“源于教材，高于教材”的命题理念之下，我们老师必须站在整体高度审视教材、钻研教材、真正地吃透教材，要结合自己对近几年的高考真题的研究，发挥自己的聪明才智去创造性地使用教材.

1.提炼归纳数学思想方法

《考试大纲》明确指出：高考对数学思想方法的考查是对数学知识在更高层次上的抽象和概括的考查.考查时必须要与数学知识相结合，通过对数学知识的考查反映学生对数学思想方法的掌握程度.

一方面，教材凝聚着许多数学家的智慧，是数学知识、方法、思想的载体，另一方面，教材是以知识的逻辑顺序为主线来编写的，方法和思想是伴随着内容主线而呈现的，这些方法和思想分散在内容之中，在复习阶段，必须对这些方法和思想进行一次提炼和归纳.如配方法、待定系数法、坐标法、反证法、数形结合思想、函数与方程思想、分类讨论思想等，要弄清这些方法和思想出现在哪些章节中，这些思想方法通常被用来解决哪些问题.对教材中有关定理，公式推导过程所涉及的思想方法也要掌握，它经常体现了知识发生和发展过程.

2.模块和章节内容之间的有机整合、相互交汇、纵横联系

高考命题者都在知识交汇处命题，用来考查学生掌握知识的全面性、系统性、深刻性.因此，在复习阶段，要打破以往教学中各模块、各章节的片断化，应通过类比、联想、迁移等方式，将各模块、各专题联系起来，让学生感受到数学的整体性，进一步理解数学本质，提高解决问题能力.如教材中基本初等函数、三角函数、数列分别在《必修1》《必修4》《必修5》中，但它们的本质都是函数，在复习时要深刻挖掘其本质联系，体会其中的思想方法.

3.典型例习题的重组、改编

每年的高考试题中，有不少试题来源于教材已是大家公认的事实，这充分体现了“源于教材，高于教材”的命题思想，也对教师的复习教学起到导向作用.在复习过程中，教师应有意识、有目的地对教材中的典型的例习题进行一次大梳理、深思、探究，挖掘其背景、内涵和外延，对其进行重组和改编、拓展和延伸.

案例 《选修2-1》第73页第6题：

如图1，直线y=x-2与抛物线y2=2x相交于A，B两点，求证：OA⊥OB.

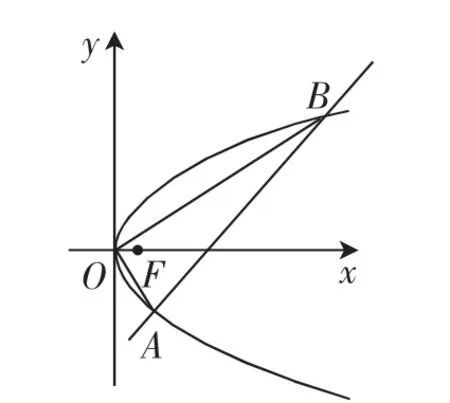
图1

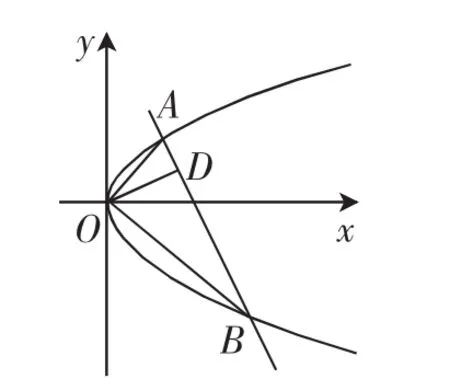
图2

姊妹题：《选修2-1》第81页第3题：

如图2，已知直线与抛物线y2=2px（p>0）交于A，B两点，且OA⊥OB，OD⊥AB交AB于D，点D（2，1），求p的值.

这两道题的共同之处实为抛物线内接三角形问题，我们可对该题进行挖掘、变式，形成题组.

将结论变为条件，可得：

变式1：已知抛物线y2=2x，A，B是抛物线上两点，且OA⊥OB.

（1）求AB中点M的轨迹方程；

（2）求证：直线AB过定点.

将原题中直线由固定变成过定点，可得：

变式2：已知过定点P（1，0）的直线l交抛物线y2=2x于A，B两点，求△AOB面积的最小值.

改变内接三角形顶点位置，可得：

变式3：已知点P（2，2），A，B是抛物线C：y2=2x上两个动点，且kPA·kPB=1，求证：直线AB过定点.

图3

图4

变式4：直角三角形ABP内接于抛物线y2=4x，顶点P（1，2），直角顶点A是动点，求点B的纵坐标的取值范围.

变式5：已知P（x0，y0）是抛物线y2=2px（p>0）上一定点，直线PA，PB的倾斜角互补，分别交抛物线于A，B两点，

（1）求证：直线AB的倾斜角的定值；

（2）△PAB的面积是否存在最大值？若存在，并求出其最大值.

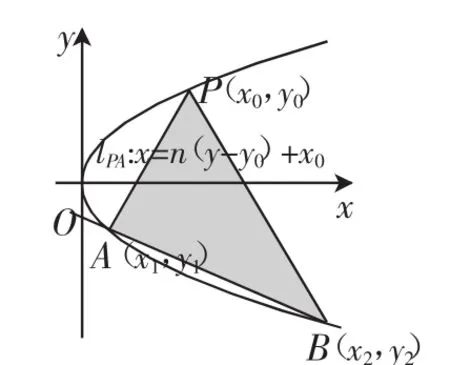
图5

图6

再延伸，拓展，引进三角形内切圆，可得：

变式6：P是曲线C：y2=x上的动点，过点P作圆M：（xt）2+y2=1的切线，分别为l1，l2，交曲线C于另两点A，B，问是否存在t∈R，使对任意的动点P，直线AB必与圆M相切？

还可以继续变下去，如可以将条件以向量形式给出，将抛物线与椭圆组合，等等.

一个变式题组下来，从易到难，一题多解，就把直线过定点问题、面积最值问题、证明问题、求轨迹问题、存在性问题都复习到了，解析几何解题的一些常规方法也都考查到了.

教材凝聚了许多数学家的集体智慧，课本上一些看似平淡无奇的例习题，隐藏着深远的背景，我们挖掘教材上的例习题，不应停留在它的表面，而应该准确把握习题的特征，探究它的本质，合理地进行拓展和延伸，通过一系列的变式，将题型和方法进行整合，拓宽学生视野，以达到对知识和方法融会贯通的目的，切实提高学生的解题能力和数学素养.

三、“看山还是山”——解题时要回归到教材的基本概念、基本原理

高三复习教学，解题教学应该占大部分课时.在解题教学过程中，我们不应该过分追求解题技巧，而应以通性通法为主，重心放在培养提高学生审题能力、分析问题能力之上，要培养学生从基本概念、基本原理及其联系性出发思考和解决问题的习惯.

结束语

回归教材是科学备考、高效复习的必然要求，是提升学生数学能力和数学素养的必然要求；如何回归教材、高效复习，是值得大家共同探究和思考的一个话题；回归教材应该是贯穿整个复习过程始终的.我们在复习阶段，不能离开教材，离开教材就会迷失方向，我们亦不能把回归教材理解为“对教材的简单重复”.我们应把教材内容及其蕴含的思想方法进行横向优化与纵向深化，不仅仅在知识上形成系统化，更应该形成从知识到方法、再到能力和数学素养的拾级而上.W