膏体料浆管道输送中粗颗粒迁移的影响因素分析

颜丙恒，李翠平，吴爱祥，王少勇，侯贺子



膏体料浆管道输送中粗颗粒迁移的影响因素分析

颜丙恒1, 2，李翠平1, 2，吴爱祥1, 2，王少勇1, 2，侯贺子1, 2

(1. 北京科技大学 土木与资源工程学院，北京 100083； 2. 北京科技大学 金属矿山高效开采与安全教育部重点实验室，北京 100083)

含粗骨料的膏体充填料浆在管道输送时存在粗颗粒沉降堵管和管壁磨损严重的问题，但常规的管道输送实验方法难以获得粗颗粒在管道截面上径向迁移的影响因素。以颗粒在黏塑性流体中的运动规律为基础，结合膏体充填工艺的实际情况，采用数值模拟研究膏体料浆流变参数对粗颗粒迁移的影响。针对实际生产中管道直径与粗骨料颗粒直径之比相对较小，在颗粒−流体耦合分析时可将粗骨料颗粒视为宏观颗粒，采用宏观颗粒模型(MPM)进行数值模拟。以Bingham流体的无量纲数，即塑性黏度雷诺数p、宾汉姆数i为定量评价指标，分析充填料浆的屈服应力、塑性黏度对粗骨料颗粒迁移的影响。结果表明，对于剪切流动区域内的粗骨料颗粒，其径向迁移量与屈服应力值和宾汉姆数i呈反比、与塑性黏度值呈正比，在一定的黏性效应下与塑性黏度雷诺数p呈正比。

膏体充填料浆；宏观颗粒模型；影响因素；流变参数；无量纲数

膏体充填具有“一废治两害”的优点，具有非常可观的发展前景。添加粗骨料的膏体充填料浆可提高固相体积分数，改善膏体流动性，增强充填体强度[1]。目前膏体充填中使用的粗骨料主要有砾石、矸石、冶炼炉渣、废弃混泥土等[2−4]。对于膏体充填料浆，多数研究认为是一种在管道输送时表现出黏性与塑性的黏塑性非牛顿流体[5−7]，常视为Herschel−Bulkley流体或Bingham流体。分析粗颗粒在膏体管道输送时的迁移规律，常以颗粒在非牛顿流体中的运动为理论基础。颗粒在牛顿流体或非牛顿流体中运动时所受的力包括阻力、压力梯度力、虚质量力、Magnus升力、Saffman升力等[8]，这些力是否考虑以及具体的计算公式，需依据流体的具体流动状态而定；颗粒相对于流体的运动受较多因素影响，如雷诺数、密度差、颗粒与管径尺寸比、颗粒浓度、流动方向、流体性质等[9−11]；颗粒迁移往往表现出朝向管道壁面、朝向管道中轴线、朝向特定管径处等形式，或者没有沿管径方向的迁移发生，并且迁移过程中表现出平移或者平移与旋转相结合的运动。在已有研究成果中，根据黏塑性流体的流速分布特性，研究颗粒在不同流速下由于剪切诱导作用所产生的沉降与径向迁移现象，发现静置条件下不易沉降的颗粒往往在剪切诱导的作用下发生沉 降[12−14]。但是因其实验条件是在较细的毛细管路中开展的，并且颗粒直径较小，雷诺数远小于1，近似为Stokes流动，惯性力远小于黏性力，所得颗粒迁移的影响因素是否适用于膏体充填料浆管道输送时粗颗粒的迁移需要进一步分析。

为此，本文作者将含粗颗粒的膏体充填料浆抽象为离散相的粗骨料颗粒与连续相的非牛顿悬浮液，针对粗骨料颗粒与非牛顿悬浮液在管道内流动时彼此相互作用复杂的特点，采用颗粒−流体耦合的数值模拟方法进行研究。Euler方法研究连续相的非牛顿流体，采用Lagrangian方法研究离散相的粗骨料颗粒。依据膏体充填料浆在管道输送时所具有的“柱塞流”特性，运用宏观颗粒模型MPM(Macroscopic particle model)计算粗骨料颗粒与非牛顿悬浮液在不同流动区域中颗粒−流体之间的相互耦合作用[15−16]，分析非牛顿悬浮液的流变参数对粗骨料颗粒运动规律的影响，选取相关无量纲数定量评价粗颗粒迁移的影响因素。

1 含粗颗粒的膏体流动理论分析

1.1 非牛顿悬浮液的流变学模型

在膏体充填料浆中，所使用的尾砂颗粒浓度较高并且与水在尾砂浓密阶段混合的相当均匀，管道输送过程中不会发生明显的尾砂颗粒与水分离的现象。此时，可以将尾砂颗粒与水共同视为一种近似均质的高浓度微细颗粒悬浮液体系，其呈现出一定的非牛顿流体特性[17]。这类高浓度悬浮液体系在流动时呈现出高黏性特点并具有屈服应力值[18]。针对这一类悬浮液体系的研究[5,7]已证明其非牛顿流变学模型主要为Bingham流变模型或者Herschel−Bulkley流变模型(屈服伪塑性流体)，其剪切应力−剪切速率方程如式(1)和(2)所示：

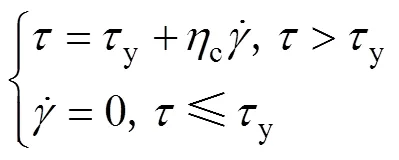
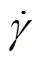
1.2 膏体管道输送中粗颗粒受力分析

尾砂颗粒与水构成的悬浮液具有非牛顿流变性，在管道输送过程中，靠近管道壁面区域的剪切速率值较大，会使此区域的表观黏度值因剪切变稀现象而逐渐变小，在管壁附近的表观黏度值变得最小，相应地降低输送时的摩擦压降[17]。同时，管道中间区域的剪切速率值较低，相应的表观黏度值最大，加上尾砂颗粒与水共同构成的悬浮液具有一定的屈服应力，有利于粗骨料颗粒在此区域内悬浮运输。考虑到含粗骨料的膏体充填料浆呈现出一定的“柱塞流”特性，即在管道的中心部位呈现近似整体平移的非剪切流动状态，而在靠近管道壁面区域呈现剪切流动状态。依据悬浮液在管道内输送时是否发生明显的剪切流动，沿管道径向可划分为剪切流动区与非剪切流动区，其流态分区示意图如图1所示。

图1 复合流动模型管道输送流态分区示意图

在非剪切流动区域内由于悬浮液的剪切速率很小基本可以忽略不计，因此，区域内颗粒周围流体介质的流速差较小1≈2，此区域内颗粒沿管径方向的位移量较小。颗粒主要受到重力的影响，如果颗粒1在此区域满足所受重力大于悬浮液在垂直方向对其的阻力V(悬浮液的剪切阻力)，则颗粒会发生一定的沉降运动，悬浮液对粗颗粒的承载能力较差。已有研究表明[13]，针对颗粒在中间柱塞流动区域内能否发生沉降，提出了相应的判别公式，如式(3)所示：

式中：为无量纲参数，其值反应塑性效应与重力效应的比较；为重力加速度，9.81 m/s2；为颗粒直径，m；Δ为颗粒与流体之间的密度差，kg/m3。对于非剪切流动区域内的沉降而言，存在一个判据值S，其值在0.048至0.111之间，当＞S时[13, 19−20]，非剪切流动区域内的颗粒不会发生沉降，否则颗粒容易发生屈服沉降现象，使颗粒在输送过程中向管道底部逐渐沉降积累，造成管道内粗颗粒堆积堵管的问题。

在剪切流动区域内由于悬浮液的剪切速率值较大不能忽略，此区域内颗粒周围流体介质的流速差较大，颗粒2两侧的流速1＞2。颗粒在此区域内与悬浮液的相对运动较为明显，存在较强的自旋运动。考虑到颗粒与流体之间的密度差，在管径方向移动的基础上还存在一定的沉降运动，但是其不会穿过中间的非剪切流动区，而是绕过中间的区域，呈现一定的螺旋线轨迹向管道底部沉降[13]。同时还需要考虑到，粗颗粒的径向移动受限于管道直径以及流体性质。管道直径对颗粒迁移规律的影响可以管道直径与颗粒直径的比值来体现，即：

式中：为无量纲参数，代表管道直径与颗粒直径的尺寸比；为管道直径，m。除了的影响外，剪切流动区的尺寸(m)与颗粒直径的比值也会影响颗粒在剪切流动区域内的迁移形式与位移量的大小。

同时考虑到雷诺数、宾汉姆数(或Oldroyd数)的影响，粗颗粒−悬浮液的相互作用非常复杂。管道输送过程中粗颗粒与非牛顿悬浮液之间的相互作用力，如阻力、压力梯度力、虚质量力、Magnus升力、Saffman升力等难以定量化进行研究。同时，颗粒与非牛顿悬浮液之间相互作用力的大小以及相应计算公式还受到非牛顿流体的流变性、管道壁面、颗粒物理参数的影响[17]。在难以开展管道输送实验的条件下，采用数值计算方法来研究粗颗粒在管道截面上迁移的影响因素具有一定的可行性。

2 数值计算方法的实现

为研究添加粗颗粒的膏体料浆在管道输送中，粗颗粒−非牛顿流体的耦合作用，需要分别分析离散的粗颗粒相以及连续的非牛顿流体相。连续的非牛顿流体相通过质量守恒方程、动量守恒方程以及流体介质的本构方程与初始边界条件来求解宏观流动行为。而离散的粗颗粒相则关注对单个颗粒的运动描述，例如离散元(Discrete element method)方法，其基于牛顿第二定律来求解颗粒运动。与基于Euler-Euler方法下的两相流模型(Two-fluid models)相比，粗颗粒−非牛顿流体的耦合应采用Euler-Lagrangian方法来研究管输过程中粗颗粒的迁移。

在一定的值下，粗颗粒−非牛顿流体耦合过程中粗颗粒的体积不可以忽略，粗颗粒体积包含多个流体计算网格，颗粒−流体、颗粒−颗粒、颗粒−管壁之间的相互作用均需考虑，为此可以采用Euler-Lagrangian耦合方案下的RDPM(Resolved discrete particle model)方法求解[21]。宏观颗粒模型MPM便是基于RDPM的一种颗粒−流体耦合方法[22]，可以确定所追踪颗粒的位移与速度等物理量，基于所研究的颗粒−流体间动量改变量求解粗颗粒与非牛顿悬浮液之间的相互作用力[16]。

2.1 宏观颗粒−非牛顿流体耦合

2.1.1 非牛顿流变学模型的数值实现

视为连续相的尾砂高浓度悬浮液属于黏塑性非牛顿流体，其流变方程如式(1)所示，非牛顿流体与牛顿流体相比最大的不同点在于偏应力张量与应变率张量之间不满足线性关系，即不满足式(5)的形式：

式中：为偏应力张量；为比例系数，一般视其为动力黏度；为应变率张量，其计算公式如式(6)：

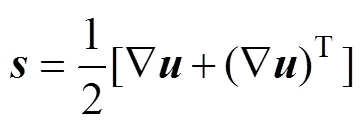
式中：为连续相速度，m/s。因此，对于非牛顿流体为计算其偏应力张量，常使用表观黏度表示即时的偏应力张量与应变率张量之间的关系，为表达出二者之间的非线性，一般为应变率张量的函数。非牛顿流体的偏应力张量与应变率张量计算公式如式(7)所示：

式中：()为表观黏度，Pa·s。对应式(7)则Cauchy应力张量与应变率张量之间的关系如式(8)：

式中：为Cauchy应力张量；为单位张量；为压力。因此连续相的动量方程如式(9)所示：

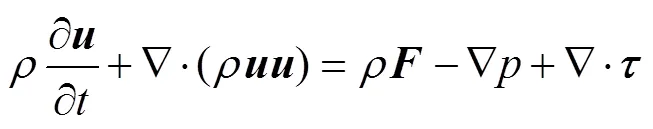
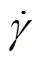
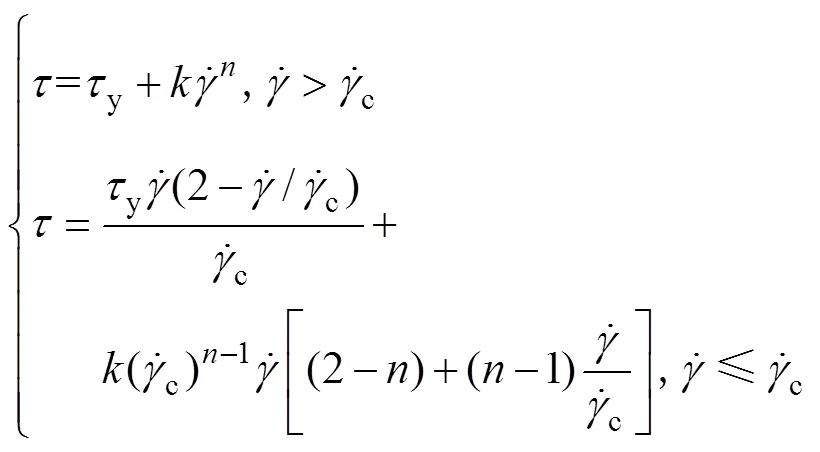
分析式(11)可知，修改后的Bingham流变方程在临界剪切速率值处，两分段函数的函数值是相同的，并且在对应的处，两分段函数对剪切速率的导数值相同。因此，式(11)在描述Bingham流体屈服应力值时，保证了流变方程的连续性，避免了数值计算的不稳定性。Bingham流变方程在ANSYS Fluent中的实现原理如图2所示。同时需要注意，尾砂高浓度悬浮液的黏度除受剪切速率值的影响，还受相应温度值变化的影响，在ANSYS Fluent中模拟Bingham流变方程时，忽略了温度变化对黏度值的影响，即不考虑温度变化对能量方程以及黏度的影响，设置流体活化能与热力学常数的比值参数为0。

2.1.2 基于RDPM方法的粗颗粒−非牛顿流体耦合实现

在研究粗颗粒−非牛顿流体耦合时，悬浮液中的粗颗粒视为刚性球体模型，即在颗粒−颗粒和颗粒−壁面碰撞过程中，粗颗粒不会发生变形。在宏观颗粒模型MPM中，允许颗粒尺寸大于计算网格的尺寸，并且不需要额外指定颗粒−流体之间的阻力、升力等模型，而是基于对颗粒表面附近流体计算单元中的速度、压力、剪切应力的积分来计算颗粒与流体之间相应的阻力、以及扭矩值的大小[15]，流体介质可指定为H−B流变模型或者Bingham流变模型[22]。因粗颗粒在管道内的迁移运动，其在不同时刻的颗粒速度将发生变化。MPM在研究运动的粗颗粒时，其是在非定常的条件下开展的。为此，在每一个计算时间步长内需要计算颗粒的速度，其速度通常包含六个分量，三个线速度分量以及三个角速度分量。在粗颗粒直径范围内所包含至少一个节点的网格，可称之为“接触”单元，“接触”单元处的速度依据体积分数权重获取，其值介于流体单元速度与粗颗粒速度之间，并且逐渐外推至粗颗粒速度值，此过程称之为粗颗粒运动速度的修正过程。在此过程中粗颗粒运动引起的动量变化也被传递至流体相中。MPM模型下，粗颗粒−非牛顿流体耦合计算框架以及粗颗粒运动速度的修正示意图如图3所示。

图3 粗颗粒−非牛顿流体耦合与粗颗粒速度修正示意图

依据牛顿第二定律，MPM模型中单位质量的粗颗粒其受力平衡方程[24]如式(12)所示：

式中：p颗粒速度，m/s；body颗粒体力(例如：重力body: mg)，N；surf颗粒−流体之间相互作用力(例如：颗粒−流体之间的阻力、升力等)，N；coll为颗粒−颗粒(coll: p−p)，颗粒−管道壁面(coll: p−w)的碰撞力，N。求解式(12)，获得粗颗粒的相应加速度值，便可计算下一个时间步长内新的速度值与位移值。同时可重新获取“接触”单元处的速度以及粗颗粒运动引起的动量变化。其中颗粒所受的面力surf(阻力、升力、扭矩)，其值可以粗颗粒周围非牛顿悬浮液的速度场、压力场、以及剪切应力场在粗颗粒的表面积分所得的虚质量力分量、压力分量、以及黏性力分量表示[25]，对应公式如式(13)：

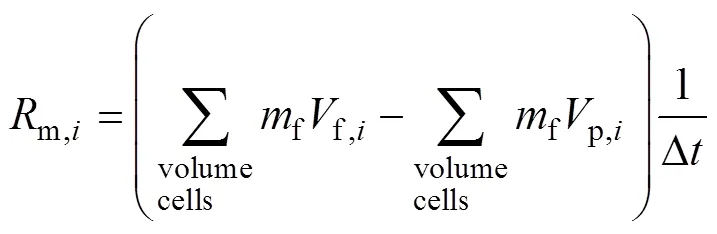
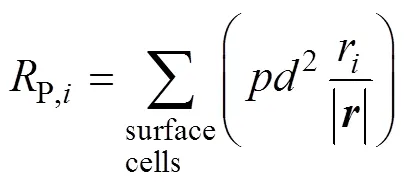
式中：f为流体单元质量，kg；f,i为非牛顿流体单元在方向上的速度，m/s；p,i为粗颗粒在方向上的速度，m/s；Δ为时间步长，s；为粗颗粒表面接触单元的压力，N；2为粗颗粒表面接触单元的近似面积，m2；为流体单元中心指向粗颗粒中心的向量；r为在方向的坐标分量，m；τ为与方向垂直的平面上沿正方向的剪切应力分量；r为在方向的坐标分量，m。

求得上述三项分量后，MPM模型将与上述计算值相等的源项添加到流体的相应控制方程中。考虑到本工作意在分析粗颗粒在管道截面上迁移的影响因素，因此重点放在粗颗粒−非牛顿流体耦合研究中，采用硬球碰撞模型求解粗颗粒之间不是很频繁的相互碰撞过程以及粗颗粒与管壁之间的碰撞过程。指定了三个参数：法相恢复系数、切向恢复系数以及摩擦因数来描述颗粒碰撞过程中的动量损耗。综上所述采用宏观颗粒模型与非牛顿流体流变模型对含粗骨料颗粒的膏体充填料浆复合流动进行数值求解，在原理上与技术上均是可行的。MPM模型作为ANSYS Fluent中的UDF模块，可以通过附加模块加载的方式调入Fluent中。其计算原理流程图如图4所示[22]。

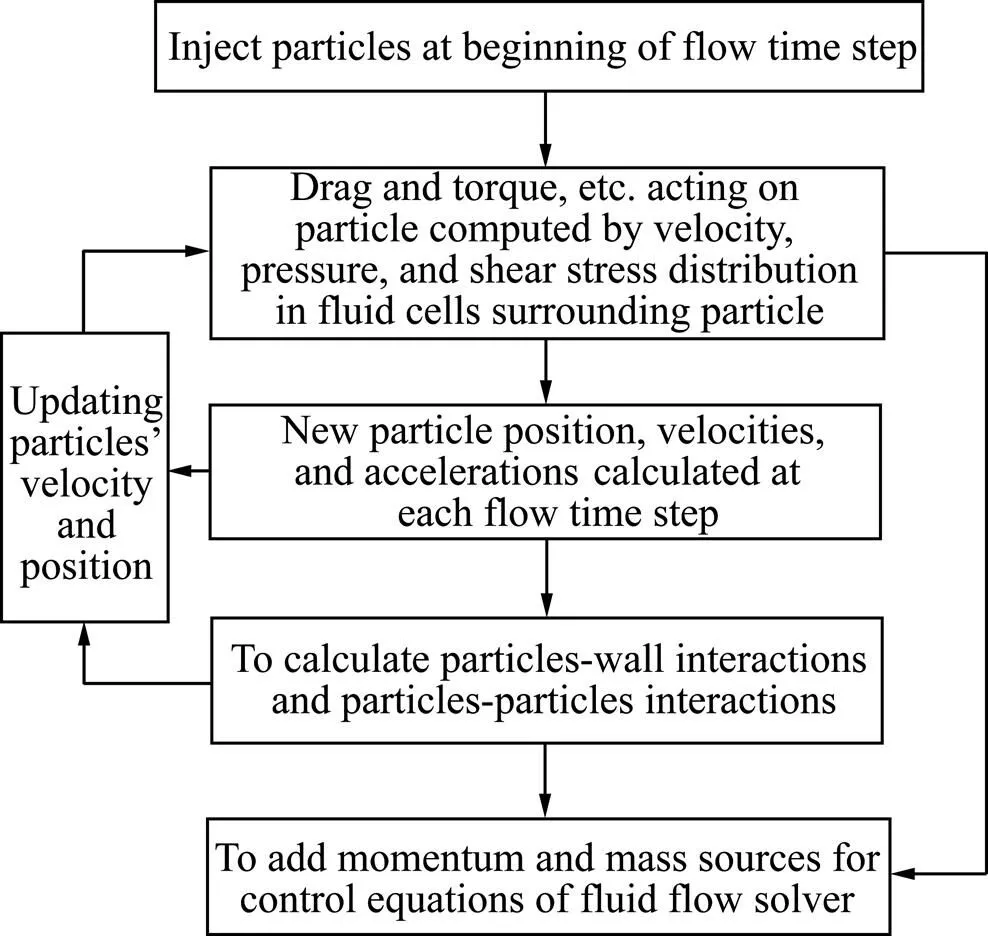
图4 MPM模型计算流程图

2.2 数值计算参数设置

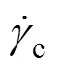
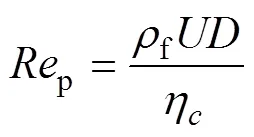
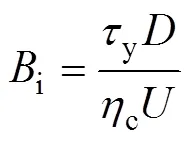
式中：p为Bingham流体的塑性黏度雷诺数，量纲为1；f为非牛顿悬浮液的密度，kg/m3；i为Bingham流体的宾汉姆数，量纲为1。将非牛顿悬浮液的各项参数以及管道尺寸参数代入式(17)和(18)，可得在屈服应力为80 Pa、塑性黏度为1.5 Pa·s的条件下，管道内Bingham流体的塑性黏度雷诺数p为120.00，宾汉姆数i为5.33。考虑到下文所研究的非牛顿悬浮液流变参数会发生变化，相应管道内塑性黏度雷诺数，以及宾汉姆数也会发生变化。这里计算了下文中屈服应力与塑性黏度变化范围内的相关无量纲数，如表1所列。

表1 对应于非牛顿悬浮液流变参数的无量纲数

依据塑性黏度雷诺数判断管道层流与湍流，由表1可知，各种流变参数条件下Bingham流体的塑性黏度雷诺数最大值为1800。对此已有研究文献中所分析的层流最大雷诺数2100[27]、2000~2500[17]和下临界雷诺数2320[28]，1800均小于以上三个阈值。因此，研究管道内的非牛顿悬浮液在剪切流动过程中的流动状态时，可以视其为层流进行研究。

2.3 数值计算独立性验证

本次数值计算的管道物理模型为一段长1 m，直径为0.1 m的直管，所加载的颗粒为球形，其直径为15 mm，加载位置距离管道入口0.2 m，所加载颗粒密度为2700 kg/m3。因RDPM方法要求所研究的颗粒包含多个流体单元，才能在不指定颗粒−流体拖曳力模型的条件下，计算二者之间的相互作用。在粗颗粒直径一定的情况下，颗粒直径范围内所包含的网格数将影响流体单元的尺寸。为验证网格独立性，选取了三种不同的粗颗粒直径与网格尺寸比，分别为3:1、5:1和8:1，使用结构体网格构建了三种管道计算域模型。采用MPM模型时，颗粒追踪的结果还受到时间步长的影响。时间步长的选取需考虑到颗粒的弛豫时间、库朗数大小以及计算时间花费三方面因素。MPM模型建议时间步长应小于其颗粒弛豫时间的1%[16]。为验证时间步长独立性，分别选取了5×10−5、1×10−5和1×10−6s这三种时间步长。

网格独立性验证以及时间步长独立性验证，均选取在0.5 s计算时长下，粗颗粒在管道中的最终位置坐标作为分析依据，即粗颗粒在管道内运动0.5 s时，位移值、位移值、位移值的大小。经过网格无关性验证与时间步长无关性验证，并在考虑可以接受的计算时间花费基础上，最终确定了可行的网格尺寸比为5:1，时间步长为1×10−5s。

3 粗骨料颗粒迁移规律的影响因素分析

3.1 非牛顿悬浮液流变参数的影响

3.1.1 屈服应力值对粗骨料颗粒迁移规律的影响

对应表1，取非牛顿悬浮液的屈服应力值依次为40、60、80、100和120 Pa，其塑性黏度值保持为1.5 Pa·s不变。对应于不同的屈服应力值，分别在管道−截面上加载两个粗骨料颗粒，其位于+轴方向上，颗粒的加载位置坐标为(0.2 m, 0 m, 0 m)与(0.2 m, 0 m, 0.03 m)。不加载颗粒的条件下，在不同屈服应力值时，管道内从轴线起沿+轴坐标方向至管壁的流速分布曲线与剪切速率分布曲线，以及在加载颗粒条件下，所加载颗粒沿+轴方向的位移值分别如图5和6所示。

由图5可知，随着屈服应力值的增加，管道中间恒速区以及零剪切速率区的宽度逐渐增加，即非剪切流动区范围逐渐增大，而剪切流动区域范围逐渐减小。这主要是因为悬浮液屈服应力值的增加，相应增大了其临界剪切速率值，使满足Bingham塑性体屈服准则条件的区域向管道壁面方向延伸，增大了非剪切流动区域的范围。由图6可知，在随屈服应力变化的过程中，在0 m处的颗粒相对位移值基本为0 m，说明了非剪切流动区域内颗粒基本不存在沿径向方向的位移；随着屈服应力值的增加，在0.03 m处的颗粒沿管道径向方向的相对位移值逐渐减少，主要原因是随着屈服界面向管壁方向的移动，颗粒两侧的剪切速率差随着屈服应力值的增加而降低，颗粒由剪切速率差引起的自旋速度变缓，从而使颗粒沿管径方向的相对位移值减少。

图5 不同屈服应力值下+Z轴方向流速分布与剪切速率分布

图6 不同屈服应力值下颗粒沿+Z轴方向的相对位移

3.1.2 塑性黏度值对粗骨料颗粒迁移规律的影响

由式(1)可知，Bingham塑性体中塑性黏度值代表了剪切应力−剪切速率曲线中的斜率值；在相同的剪切速率增量下，较大的塑性黏度值引起较大的剪切应力增量，因此，塑性黏度值对于剪切流动区域与非剪切流动区域的相对范围也存在着影响。对应表1，取非牛顿悬浮液的屈服应力值为80 Pa保持不变，塑性黏度值依次取0.1、0.3、0.5、0.7、0.9、1.1、1.3、1.5、1.7和1.9 Pa·s，在0.03 m处加载颗粒。不加载颗粒的条件下，在不同塑性黏度值时，管道内从轴线起沿+轴坐标方向至管壁的流速分布曲线以及剪切速率分布曲线如图7所示。在0.03 m处所加载颗粒沿+轴方向的相对位移值如图8所示。

图7 不同塑性黏度值下+Z轴方向流速分布与剪切速率分布

图8 不同塑性黏度值下颗粒沿+Z轴方向的相对位移

由图7可知，随着塑性黏度值的增大，中间恒速区以及零剪切速率区的宽度逐渐减小，管道沿径向的剪切流动区域逐渐增大，而非剪切流动区域逐渐减小。主要原因如下：对于恒定的管道平均流速，在相同剪切速率变化量的条件下，塑性黏度较大的悬浮液相比于塑性黏度较小的悬浮液对应的剪切应力增量也较大，在从管道中心至管道壁面剪切应力变化的过程中，其剪切应力能较快地达到屈服准则的要求，因此非剪切流动区范围较小。由图8可知，在0.03 m处加载的颗粒，其径向位移随着塑性黏度的增大而不断增大。这主要因为随着屈服界面向管道轴线方向的移动，所加载颗粒附近的剪切速率差随着塑性黏度的增大而增加，使颗粒两侧由流速差而引起的径向位移量逐渐增大。

3.1.3 宾汉姆数i对粗骨料颗粒迁移规律的影响

为综合考虑悬浮液的塑性黏度值与屈服应力值对剪切流动区域内颗粒沿径向位移的影响，使用无量纲的宾汉姆数来研究悬浮液流变参数变化对颗粒径向位移的影响。对应表1，上述两节不同宾汉姆数i下，在0.03 m处所加载的颗粒沿径向位移值随宾汉姆数的变化情况如图9所示。

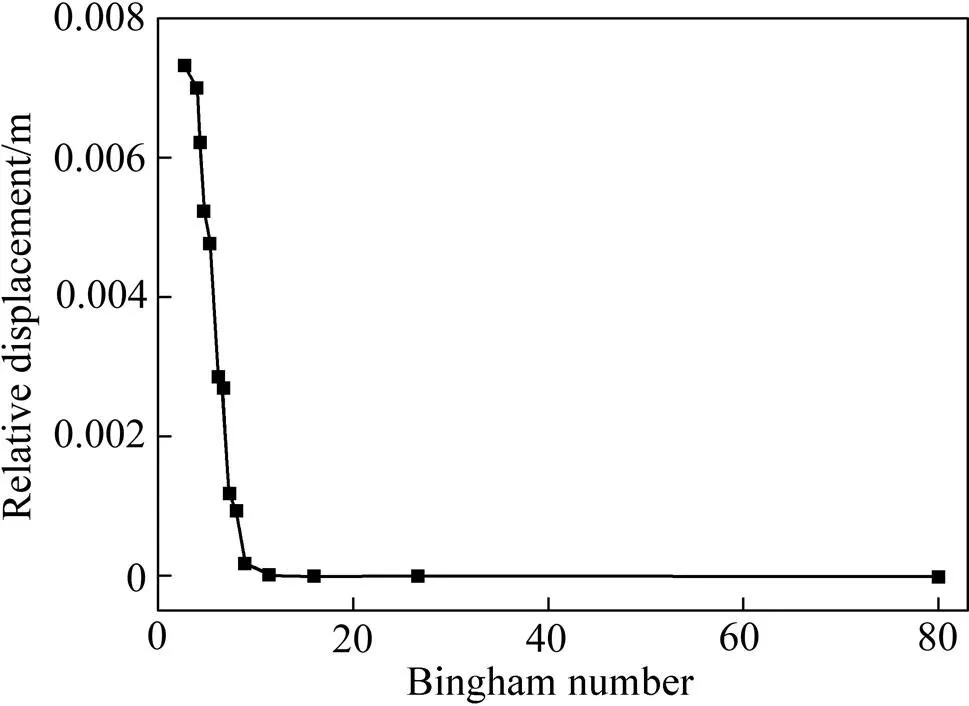
图9 不同宾汉姆数下颗粒沿+Z轴方向的相对位移

由图9可知，颗粒沿径向的位移随宾汉姆数的增加而减小，并且在宾汉姆数为10左右下降幅度最为明显，此时有屈服应力与塑性黏度的(80 Pa, 0.9 Pa·s)和(80 Pa, 0.7 Pa·s)两种组合情况。在这两种组合下，0.03 m处颗粒位移基本为0 m。在一定的管径、管速与颗粒物理参数条件下，颗粒发生运动的临界面为0.03 m，大于此值时颗粒将在剪切流动区域内发生较为明显的运动。

3.2 管道平均流速对粗骨料颗粒迁移规律的影响

对应表1，取悬浮液的屈服应力为80 Pa，塑性黏度分别为0.5 Pa·s和1.5 Pa·s，在+0.03 m处加载直径为15 mm的粗颗粒。同时分别设定管道入口处的平均流速为0.7、1.0和1.3 m/s，粗颗粒沿轴的相对位移如图10所示。

图10 不同管道平均流速下颗粒沿+Z轴方向的相对位移

由图10可知，塑性黏度为0.5 Pa·s时，在0.03 m处加载的颗粒沿管径方向的相对位移值基本为0 m，此时处于非剪切流动区域内，管道平均流速对其在径向方向上的运动基本无影响。对应不同的平均流速0.7、1.0和1.3 m/s，其塑性黏度雷诺数p分别为252、360和468，其颗粒径向位移量均接近0 m，可见在一定的黏性效应下，流动形式为层流状态时，Bingham流体的塑性黏度雷诺数对颗粒径向迁移运动影响较小。而在塑性黏度为1.5 Pa·s时，在0.03 m处加载的颗粒沿管径方向的相对位移值随着管道平均流速的增加而增大，此时塑性黏度雷诺数分别为84、120和156，流动形式为层流状态，颗粒的径向位移量随着p的增大而增大，说明在特定的黏性效应下，惯性效应促进颗粒的径向位移。

4 结论

1) 针对含粗颗粒的膏体充填料浆管道输送特性，依据剪切速率的相对大小划分了剪切流动区与非剪切流动区。采用宏观颗粒模型MPM，分别针对两个区域内颗粒运动的特点进行了数值计算，研究粗颗粒迁移的影响因素。

2) 粗颗粒在剪切流动区域内的径向位移与悬浮液的屈服应力值呈负相关性，而与塑性黏度值呈正相关性。为此，可以通过提高悬浮液的屈服应力值或降低塑性黏度值来减小输送时的剪切流动区域，避免过多颗粒在此区域内移向壁面并向管底迁移，造成堵管事故。

3) 通过悬浮液的塑性黏度雷诺数p与宾汉姆数i来综合反映惯性效应(管道平均流速)、黏性效应(塑性黏度)和塑性效应(屈服应力值)对粗颗粒径向迁移的影响。宾汉姆数i与颗粒径向位移呈负相关性，并且存在一个突变的临界宾汉姆数影响颗粒的径向迁移，本研究中，此临界宾汉姆数约为10。在层流状态下，塑性黏度雷诺数p对颗粒径向迁移的影响是发生在一定的黏性效应之下的，在颗粒存在径向迁移的条件下，其值与颗粒迁移量呈正相关性。

[1] 吴爱祥, 王洪江. 金属矿膏体充填理论与技术[M]. 北京: 科学出版社, 2015: 25−43. WU Ai-xiang, WANG Hong-jiang. The theory and technology of metal ore paste backfill[M]. Beijing: Science Press, 2015: 25−43.

[2] 王洪江, 李公成, 吴爱祥, 杨 鹏, 彭乃兵, 杨锡祥, 周发陆. 不同粗骨料的膏体流变性能研究[J]. 矿业研究与开发, 2014, 34(7): 59−62. WANG Hong-jiang, LI Gong-cheng, WU Ai-xiang, YANG Peng, PENG Nai-bing, YANG Xi-xiang, ZHOU Fa-lu. Study on rheological properties of paste with different coarse aggregate[J]. Mining Research and Development, 2014, 34(7): 59−62.

[3] 冯国瑞, 贾学强, 郭育霞, 戚庭野, 李 典, 李 振, 冯佳瑞, 刘国艳, 宋凯歌, 康立勋. 废弃混凝土粗骨料对充填膏体性能的影响[J]. 煤炭学报, 2015, 40(6): 1320−1325. FENG Guo-rui, JIA Xue-qiang, GUO Yu-xia, QI Ting-ye, LI Dian, LI Zhen, FENG Jia-rui, LIU Guo-yan, SONG Kai-ge, KANG Li-xun. Influence of the wasted concrete coarse aggregate on the performance of cemented paste backfill[J]. Journal of China Coal Society, 2015, 40(6): 1320−1325.

[4] 王洪江, 吴爱祥, 肖卫国, 曾普海, 吉学文, 严庆文. 粗粒级膏体充填的技术进展及存在的问题[J]. 金属矿山, 2009(11): 1−5. WANG Hong-jiang, WU Ai-xiang, XIAO Wei-guo, ZENG Pu-hai, JI Xue-wen, YAN Qing-wen. The progresses of coarse paste fill technology and its existing problem[J]. Metal Mine, 2009(11): 1−5.

[5] 刘晓辉. 膏体流变行为及其管流阻力特性研究[D]. 北京: 北京科技大学, 2015: 48−68. LIU Xiao-hui. Study on rheological behavior and pipe flow resistance of paste backfill[D]. Beijing: University of Science and Technology Beijing, 2015: 48−68

[6] 吴爱祥, 焦华喆, 王洪江, 李 辉, 仪海豹, 刘晓辉, 刘斯忠. 膏体尾矿屈服应力检测及其优化[J]. 中南大学学报(自然科学版), 2013, 44(8): 3370−3376. WU Ai-xiang, JIAO Hua-zhe, WANG Hong-jiang, LI Hui, YI Hai-bao, LIU Xiao-hui, LIU Si-zhong. Yield stress measurements and optimization of paste tailings[J]. Journal of Central South University (Science and Technology), 2013, 44(8): 3370−3376.

[7] BOGER D V. Rheology and the resource industries[J]. Chemical Engineering Science, 2009, 64(22): 4525−4536.

[8] 岳湘安. 液−固两相流基础[M]. 北京: 石油工业出版社, 1996: 64−96. YUE Xiang-an. Liquid−Solid two−phase flow foundation[M]. Beijing: Petroleum Industry Press, 1996: 64−69.

[9] FENG J, HU H H, JOSEPH D D. Direct simulation of initial value problems for the motion of solid bodies in a Newtonian fluid (Part 1): Sedimentation[J]. Journal of Fluid Mechanics, 1994, 261: 95−134.

[10] JOSSIC L, BRIGUET A, MAGNIN A. Segregation under flow of objects suspended in a yield stress fluid and NMR imaging visualisation[J]. Chemical Engineering Science, 2002, 57(3): 409−418.

[11] MATAS J P, MORRIS J F, GUAZZELLI E. Lateral forces on a sphere[J]. Oil & Gas Science and Technology, 2004, 59(1): 59−70.

[12] MERKAK O, JOSSIC L, MAGNIN A. Dynamics of particles suspended in a yield stress fluid flowing in a pipe[J]. AIChE Journal, 2008, 54(5): 1129−1138.

[13] MERKAK O, JOSSIC L, MAGNIN A. Migration and sedimentation of spherical particles in a yield stress fluid flowing in a horizontal cylindrical pipe[J]. AIChE Journal, 2009, 55(10): 2515−2525.

[14] OVARLEZ G, BERTRAND F, COUSSOT P, CHATEAU X. Shear-induced sedimentation in yield stress fluids[J]. Journal of Non-Newtonian Fluid Mechanics, 2012, 177: 19−28.

[15] AGRAWAL M, BAKKER A, PRINKEY M T. Macroscopic particle model—Tracking big particles in CFD[C]//Proceedings of AIChE 2004 Annual Meeting, Austin, 2004, 268b.

[16] OOKAWARA S, AGRAWAL M, STREET D, OGAWA K. Quasi-direct numerical simulation of lift force-induced particle separation in a curved microchannel by use of a macroscopic particle model[J]. Chemical Engineering Science, 2007, 62(9): 2454−2465.

[17] CHHABRA R P, RICHARDSON J F. Non-Newtonian flow in the process industries: fundamentals and engineering applications[M]. Oxford: Butterworth-Heinemann, 1999: 207−255.

[18] SOFRA F. Rheological properties of fresh cemented paste tailings[M]. YILMAZ E, FALL M. Paste Tailings Management. Berlin: Springer, Cham, 2017: 33−57.

[19] ATAPATTU D D, CHHABRA R P, UHLHERR P H T. Creeping sphere motion in Herschel-Bulkley fluids: Flow field and drag[J]. Journal of Non-Newtonian Fluid Mechanics, 1995, 59: 245−265.

[20] MERKAK O, JOSSIC L, MAGNIN A. Spheres and interactions between spheres moving at very low velocities in a yield stress fluid[J]. Journal of Non-Newtonian Fluid Mechanics, 2006, 133: 99−108.

[21] VAN DER HOEF M A, VAN SINT ANNALAND M, DEEN N G, KUIPERS J A M. Numerical simulation of dense gas-solid fluidized beds: A multiscale modeling strategy[J]. Annual Review of Fluid Mechanics, 2008, 40: 47−70.

[22] WADNERKAR D, AGRAWAL M, TADE M O, PAREEK V. Hydrodynamics of macroscopic particles in slurry suspensions[J]. Asia−Pacific Journal of Chemical Engineering, 2016, 11(3): 467−479.

[23] MITSOULIS E. Flows of viscoplastic materials: Models and computations[J]. Rheology Reviews, 2007, 2007: 135−178.

[24] SORIA J, GAUTHIER D, FLAMANT G, RODRIGUEZ R, MAZZA G.Coupling scales for modelling heavy metal vaporization from municipal solid waste incineration in a fluid bed by CFD[J]. Waste Management, 2015, 43:176−187.

[25] AGRAWAL M. Drag force formulation in macroscopic particle model and its validation[C]//Proceedings of AIChE 2009 Annual Meeting, Nashville, 2009, 163b.

[26] 陈松贵. 宾汉姆流体的LBM–DEM方法及自密实混凝土复杂流动研究[D]. 北京: 清华大学, 2014: 69−73. CHEN Song-gui. Development of LBM-DEM for Bingham suspensions with application to self-compacting concrete[D]. Beijing: Tsinghua University, 2014: 69−73.

[27] WASP E J, KENNY J P, GANDHI R L. Solid−liquid flow slurry pipeline transportation[M]. Stafa–Zurich: Trans Tech Publications Ltd., 1977: 51−56.

[28] 谢振华, 宋存义. 工程流体力学[M]. 北京: 冶金工业出版社, 2007: 67−91. XIE Zhen-hua, SONG Cun-yi. Engineering fluid mechanics[M]. Beijing: Metallurgical Industry Press, 2007: 67−91.

Analysis on influencing factors of coarse particles migration in pipeline transportation of paste slurry

YAN Bing-heng1, 2, LI Cui-ping1, 2, WU Ai-xiang1, 2, WANG Shao-yong1, 2, HOU He-zi1, 2

(1. School of Civil and Resource Engineering, University of Science and Technology Beijing, Beijing 100083, China; 2. State Key Laboratory of High-Efficient Mining and Safety of Metal Mines, Ministry of Education, Beijing 100083, China)

The paste backfill slurry with coarse aggregate had the problems of coarse particles settlement and wall wear serious in pipeline transportation. It was difficult to analyze the influencing factors of coarse particles’ radial migration in the pipeline sections by conventional pipe flow experiments. In this work, based on the law of movement of particles in viscoplastic fluid and the actual situation of paste backfill technology, the influence of rheological parameters of paste slurry on coarse particles’ law of migration was studied by numerical simulation. For actual production, the ratioof pipe diameter to coarse aggregate particles diameter was relatively small, coarse aggregate particles could be regarded as macroscopic particles in particle-fluid coupling analysis, and the Macroscopic Particle Model (MPM) was used for numerical simulation. Taking the dimensionless numbers of Bingham fluid, i.e., plastic viscosity Reynolds numberpand Bingham numberias quantitative evaluation indexes, the influence of yield stress and plastic viscosity of backfill slurry on coarse aggregate particles’ law of migration was analyzed. The results show that the radial migration of coarse aggregate particles in the shear flow region is inversely proportional to the yield stress value and Bingham numberi, is directly proportional to the plastic viscosity value, and is directly proportional to the plastic viscosity Reynolds numberpunder a certain viscous effect.

paste backfill slurry; macroscopic particle model; influencing factors; rheological parameter; dimensionless numbers

Project(2017YFC0602903) supported by the National Basic Research Development Program of China; Project(51774039) supported by the National Natural Science Foundation of China

2018-03-29;

2018-07-25

LI Cui-ping; Tel: +86-10-62334756; E-mail: cpli@ustb.edu.cn

国家重点研发计划资助项目(2017YFC0602903)；国家自然科学基金资助项目(51774039)

2018-03-29；

2018-07-25

李翠平，教授，博士；电话：010-62334756；E-mail: cpli@ustb.edu.cn

10.19476/j.ysxb.1004.0609.2018.10.23

1004-0609(2018)-10-2143-11

TD853

A

(编辑 何学锋)