基于人工神经网络模型的含锑硫化矿氧化浸出行为预测

田庆华，洪建邦，辛云涛，郭学益



基于人工神经网络模型的含锑硫化矿氧化浸出行为预测

田庆华1, 2, 3，洪建邦1，辛云涛1，郭学益1, 2, 3

(1. 中南大学 冶金与环境学院，长沙 410083； 2. 有色金属资源循环利用湖南省重点实验室，长沙 410083； 3. 有色金属资源循环利用湖南省工程研究中心，长沙 410083)

锑的浸出率是氧化处理含锑硫化矿时的重要结论指标，在氧化浸出过程中通过条件控制来得到更好的浸出率具有十分重要的意义，为了模拟和预测含锑硫化矿的氧化浸出过程，用人工神经网络模型对浸锑过程进行模拟，建立起单隐层8节点的“5-8-1型”误差逆向传播神经网络模型，所建人工神经网络模型可以对反应过程做出有效的模拟和预测，实验值与预测值的相关系数可达99%以上。并根据所建神经网络模型中不同输入量在网络中节点权重的不同，得出相关条件因素对锑浸出率的相对重要性从高到低依次为：盐酸浓度，反应温度，搅拌速度，液固比，反应时间。

人工神经网络；浸锑过程；预测；相关系数；相对重要性

我国的锑资源十分丰富，锑的储量占全球80%，也是全球第一锑生产大国[1]。工业上，从硫化锑矿中提取金属锑的方法主要有火法和湿法[2]。传统火法炼锑主要包括鼓风炉挥发熔炼和反射炉还原熔炼两个工序[3−4]。但是火法炼锑过程中会产生大量SO2，严重污染环境。湿法炼锑又分为碱法与酸法[5]，湿法炼锑因其锑回收效率高，污染小得到了众多研究者的关注。而浸出过程是湿法冶金的一个重要单元，浸出率越高则金属提取率越高，企业也能获得更好的效益[6]。

锑的浸出率是氧化处理含锑硫化矿时的重要结论指标[7]，因此在氧化浸出过程中通过条件控制来获得更好的浸出率具有十分重要的意义。目前就臭氧协同氧化处理含锑硫化矿的浸出过程并无相关理论模型进行阐述和说明[8]。对于相关广义的非线性系统的控制和模拟，特别是很难通过数学模型模拟的系统，人工神经网络是一种有效的计算和模拟手段。为了优化臭氧协同氧化浸出过程，拟采用人工神经网络对本反应过程进行模拟[9−10]。

人工神经网络可以满足非线性数据或者信号的输入、输出模式，已经广泛应用于复杂非线性过程的模型建立和控制[11]。为了优化氧化浸出过程，使用神经网络模型预测臭氧协同氧化浸出锑的效率，训练成功的神经网络模型为氧化浸出过程的优化提供具有价值的参考信息[12]。本研究的目的是使用人工神经网络的方法建模含锑硫化矿臭氧协同氧化浸锑过程中的几个操作变量，为浸出过程提供参考和借鉴。

1 BP神经网络

神经网络具有强大的并行分布处理信息的系统，具备与人脑类似的网络特点，由输入数据、神经元和输出数据组成[13]。目前已有各种类型的人工神经网络，比如径向基神经网络、广义回归神经网络和误差逆向传播神经网络等等[14]。其中BP神经网络(误差逆向传播神经网络)是一种按照误差逆向传播算法训练的具有多层的神经网络，是目前应用比较广泛的非线性神经网络模型，它通过前向传播不断地调整神经网络的权重，首先调整隐层与输出层之间的权值，在顺着方向向前依次进行调整，最后调整输入层与隐层之间的权值，使网络的平均方差值最小，其学习方法属于最速下降法[15−16]。采用误差逆向传播神经网络对臭氧协同氧化浸出含锑硫化矿中锑的反应过程进行模拟，误差逆向传播神经网络示意图如图1所示。

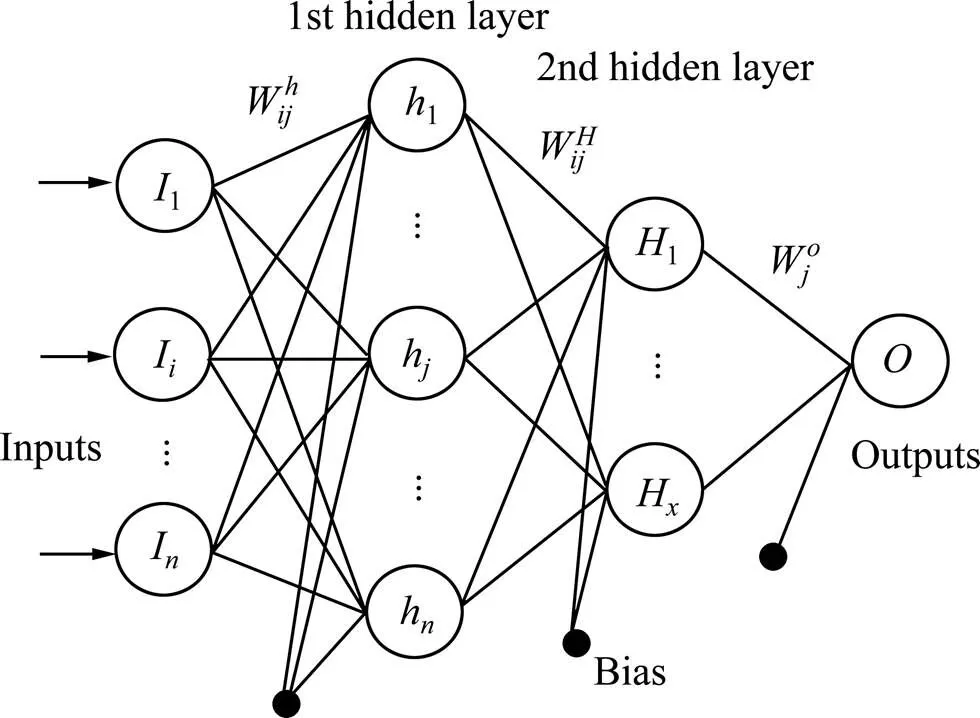
图1 神经网络的结构层次

从图1中可以看出，误差逆向传播神经网络具备输入层节点、隐层节点和输出层节点，其中隐层节点为层，≥1。数据信息通过输入层进入网络，传至隐层节点后，经过相关作用函数处理后，将隐层节点的输出信号传播至输出层节点，得到经过神经网络处理后的输出结果。当然，BP神经网络也具有一定的局限性，主要表现在：1) 需要的训练参数较多，训练参数的选择没有优化的方法；2) 容易陷入局部最优，可以通过调整初始输入值或者改变算法来规避；3) 样本的依赖性，模型的建立与所选样本的代表性具有密切关系，要求所用样本具有代表性；4) 初始权重敏感，训练开始时会随机赋值一个随机初始权重，由于是随机改动的，BP网络往往具有不可重复性[17]。

2 神经网络预测模型

2.1 神经网络预测模型的建立

如图2所示，为使用神经网络预测臭氧协同氧化处理含锑硫化矿浸锑效率的流程和步骤。开始时对相关数据进行处理，之后进行网格训练，使输入数据和目标数据归化，使其在−1~1之间[18]。网格训练完成后，输出数据转回到同格单元与起始目标进行比较。神经网络建模过程在matlab软件中进行。

评价神经网络的预测性能的优劣能通常考察3种指标，即决定系数(2)、平均方差(MSE)和平均绝对误差(MAE)[19]。如果决定系数为1左右，平均方差和平均绝对误差接近于0，可以认为神经网络的预测结果较为准确，决定系数越接近1或者平均方差/平均绝对误差越接近于0，则预测结果则越准确。决定系数、平均方差和平均绝对误差见下式所示：

MSE=(1/)´S(t−o)2(1)

MAE=(1/)´S½(t−o)½(2)

2=1−[S(t−o)2/S(o)2] (3)

式中：t是模式的输出值；o是模式的目标值；为训练库/数据库的总数量值。

图2 神经网络数据处理与训练流程

2.2 数据的选择及处理

基于实验数据而建立BP神经网络模型，共有76组数据点，随机选择其中的52组作为训练组数据，12组作为测试组数据，另外12组作为预测组数据，分别如下表1、2和3所列。实验结果(锑的浸出率)与对应的实验条件(温度、时间、液固比、搅拌速度和盐酸浓度)分别为输入向量矩阵和目标向量矩阵。在数据处理之前通常会进行预处理过程，经过预处理，神经网络模型会更加有效和准确，因此将输入数据和输出数据按照下列公式(4)进行归一化预处理[20−21]。

p=(p−mean,p)/std,p(4)

式中：p是实际的数据；mean,p是实际数据的平均值；std,p是实际数据的标准偏差；p即为处理后归一化的参数。

由于神经网络的非线性特征使其广泛应用于复杂非线性过程的模型建立和控制，其关键在于在神经网络中隐层与输出层之间使用的非线性的转化函数，常用的函数为tan-sigmoid，其表达式(5)如下所示。

()=[exp()−exp(−)]/[exp()+exp(−)] (5)

不同的算法对于整个神经网络的泛化能力具有不同的影响，Levenberg-Marquardt算法(LM)属于最优化算法中的一种，这里最优化的意为寻找使得函数值最小的参数向量，它是利用梯度求得极值(最大或者最小)的算法，同时具备牛顿法和梯度法的特点。而神经网络训练的目标和任务也是无约束的最小化并以平均方差作为评价标准，因此，这里的神经网络采用LM算法来训练所建模型[22]。

表1 训练过程所选数据列表

Table 1 Data in training process

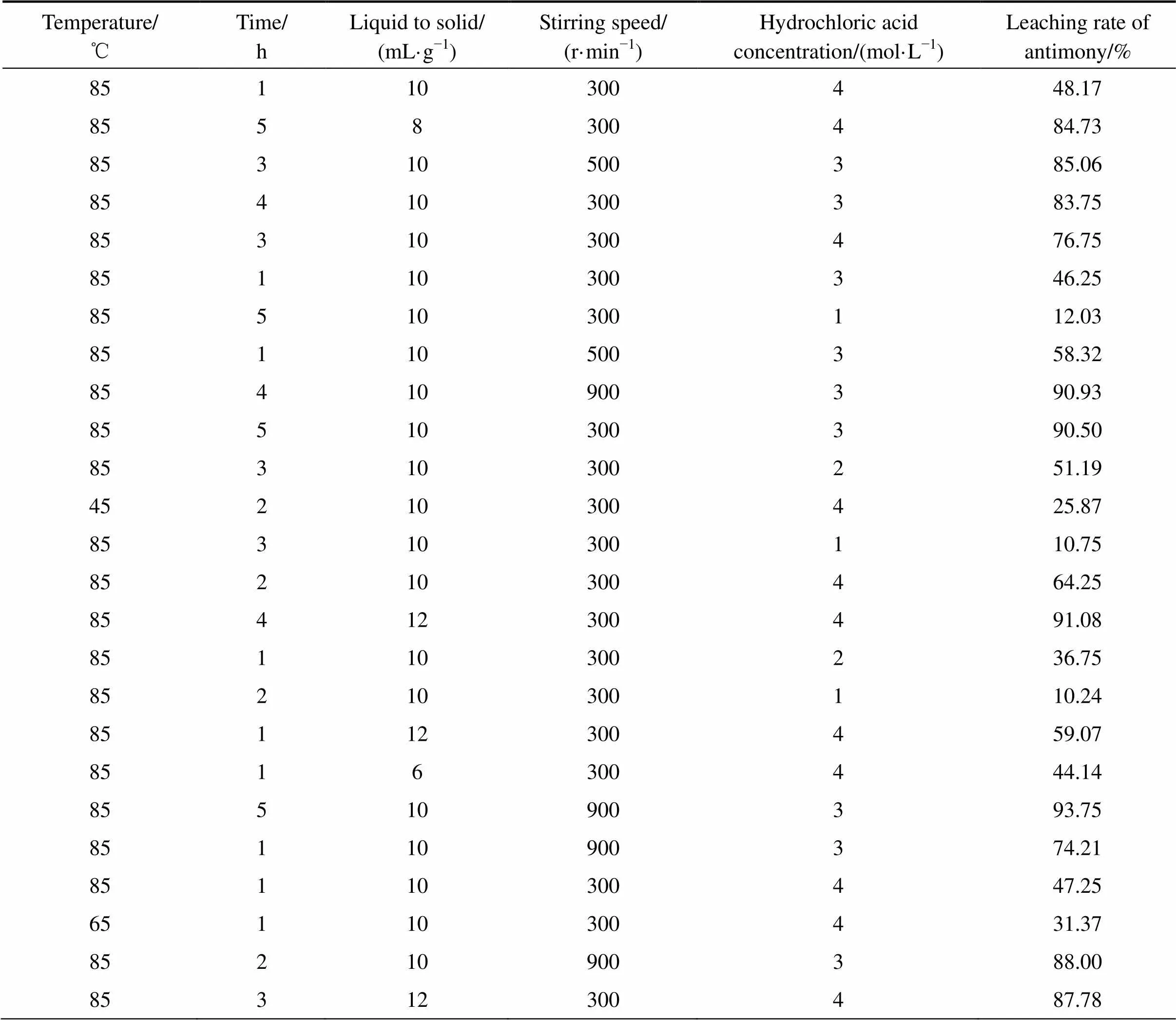
Temperature/℃Time/hLiquid to solid/(mL·g−1)Stirring speed/(r·min−1)Hydrochloric acid concentration/(mol·L−1)Leaching rate of antimony/% 85110300448.17 8558300484.73 85310500385.06 85410300383.75 85310300476.75 85110300346.25 85510300112.03 85110500358.32 85410900390.93 85510300390.50 85310300251.19 45210300425.87 85310300110.75 85210300464.25 85412300491.08 85110300236.75 85210300110.24 85112300459.07 8516300444.14 85510900393.75 85110900374.21 85110300447.25 65110300431.37 85210900388.00 85312300487.78

To be continued

Continued

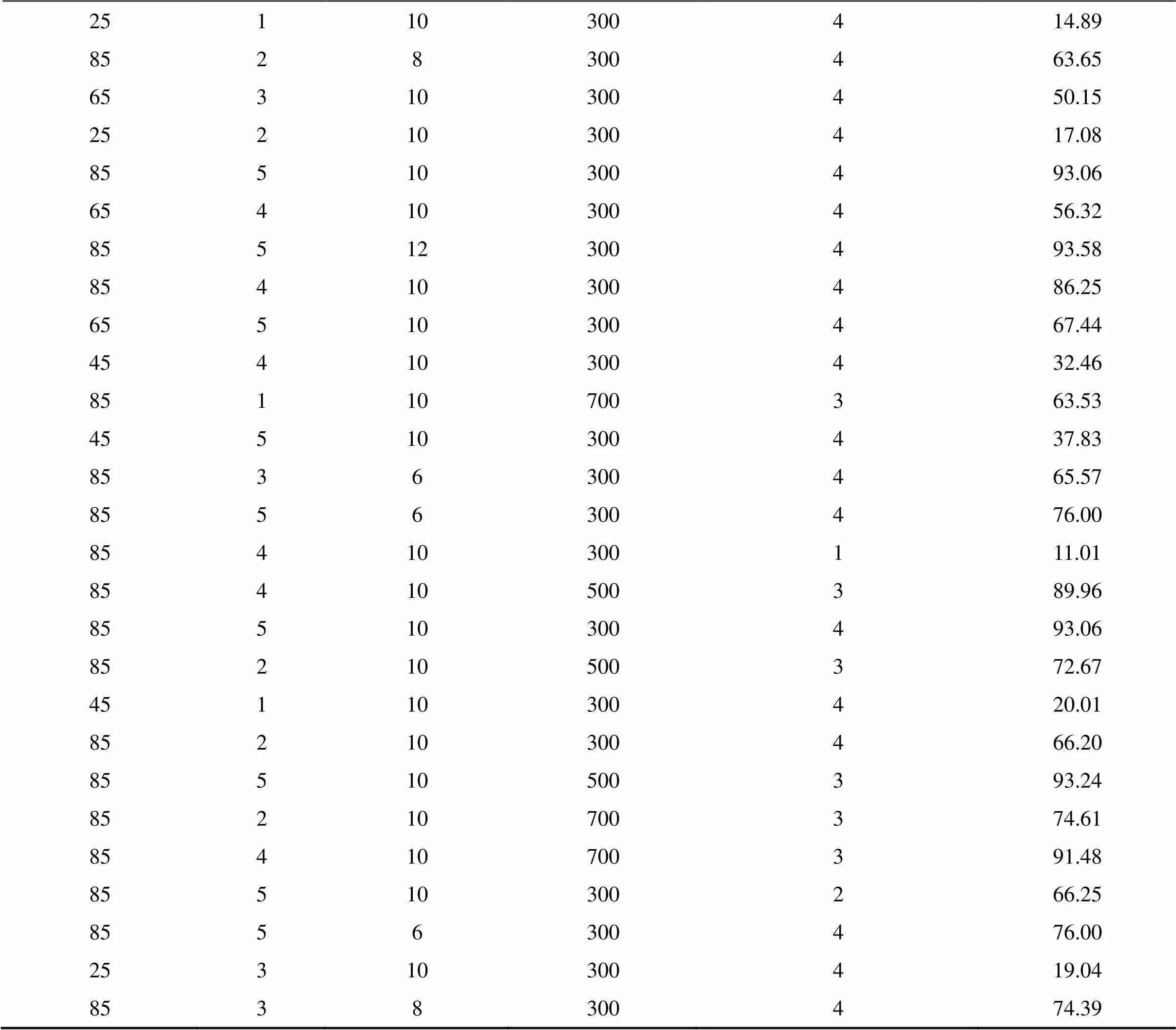
25110300414.89 8528300463.65 65310300450.15 25210300417.08 85510300493.06 65410300456.32 85512300493.58 85410300486.25 65510300467.44 45410300432.46 85110700363.53 45510300437.83 8536300465.57 8556300476.00 85410300111.01 85410500389.96 85510300493.06 85210500372.67 45110300420.01 85210300466.20 85510500393.24 85210700374.61 85410700391.48 85510300266.25 8556300476.00 25310300419.04 8538300474.39

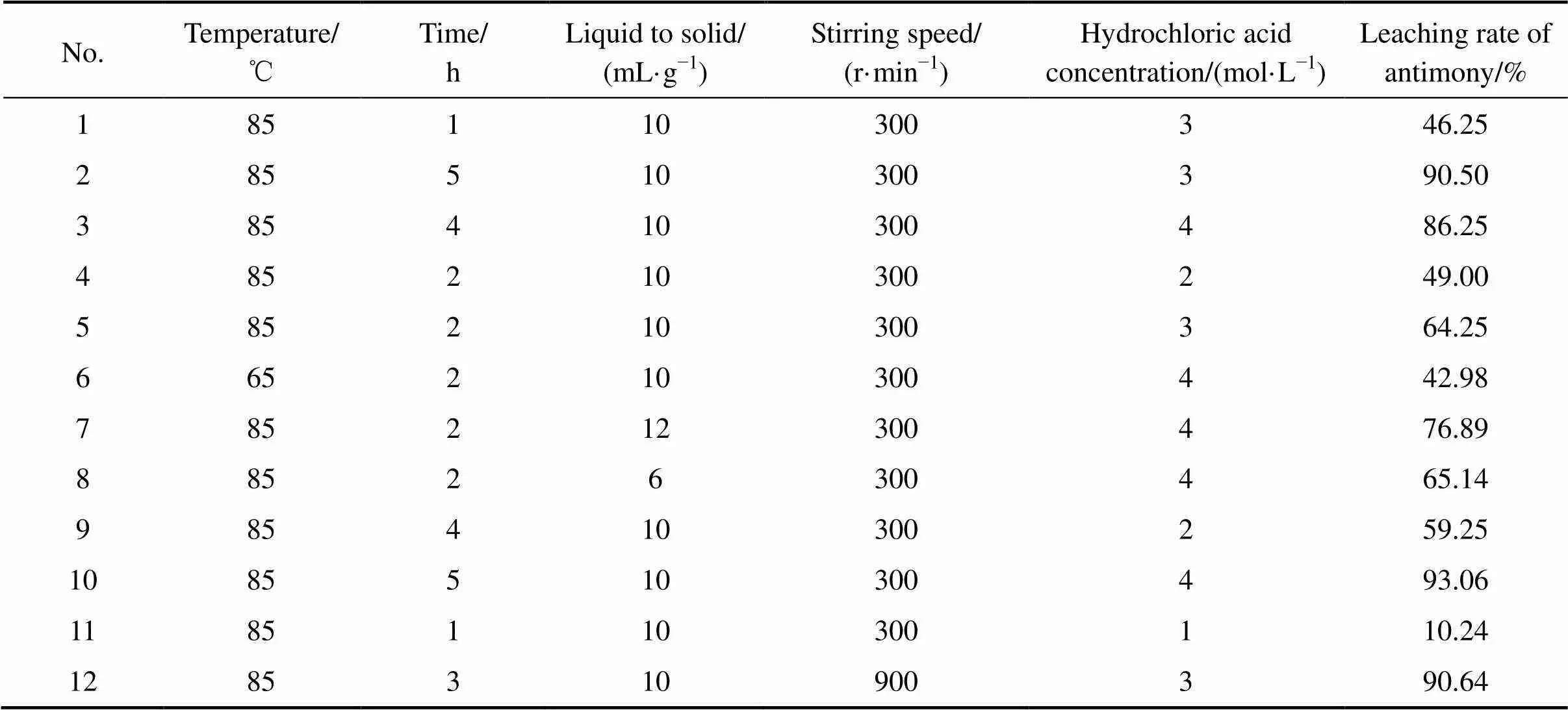
表2 验证过程所选数据列表

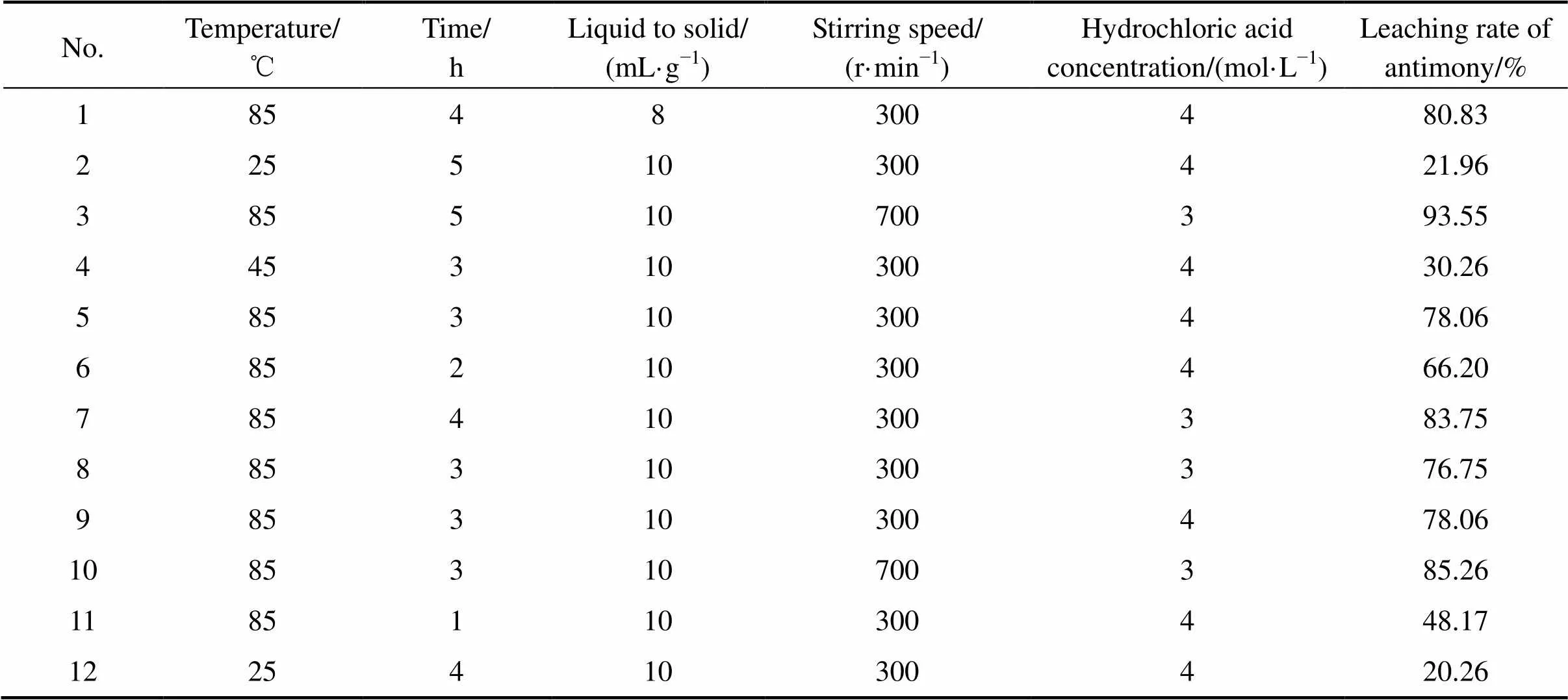
表3 预测过程所选数据列表

3 结果分析

3.1 人工神经网络的性能测试结果

BP神经网络模型的建立时通常不会采用多个隐层，而是只选择一个隐层，通过改变隐层节点数(神经元个数)来到达较好的预测结果[23]。通常神经元个数越多，其拟合性越好，但是过多的神经元个数会造成神经网络记忆僵化而忽视其相关特征，从而造成其预测能力(泛化能力)下降，因此选择合适的神经元个数比较重要[24]。在确定最佳隐层节点数(神经元个数)时，使用了多层的网络拓扑结构，节点数从5到10，图3所示为节点数对人工神经网络预测性能的影响，以MSE值较低为优。

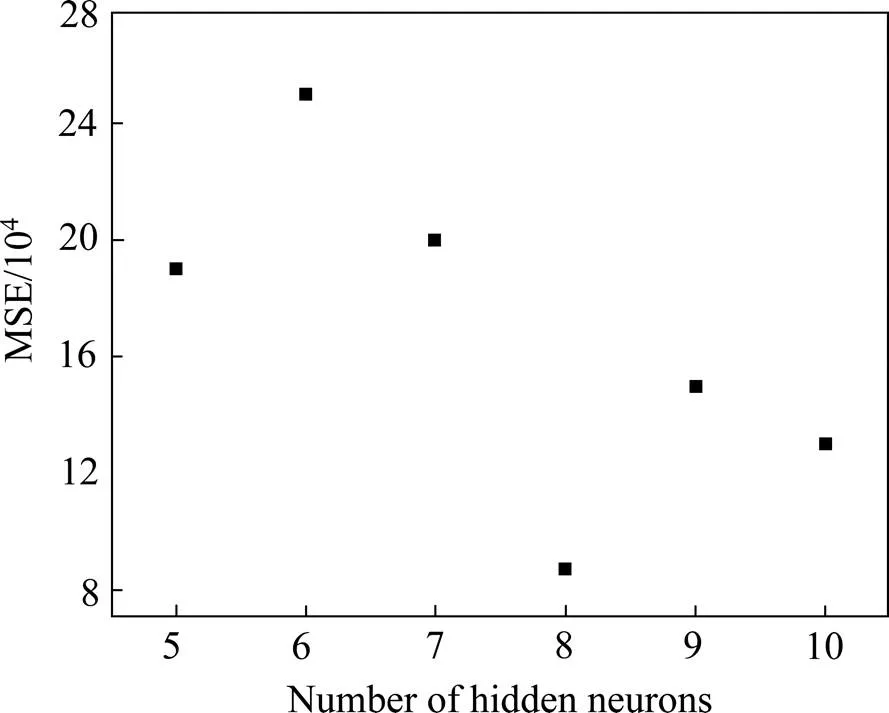
图3 节点数对神经网络预测性能的影响

从图3中可以看出，随着节点数从5增加到8，预测性能指标明显提高，之后继续增加节点数，并不能提高网络的预测性能，因此选择隐层节点数8为最佳条件，此时所训练数据的平均方差为8.7×10−4，因此选择单隐层8节点的“5-8-1型”结构用于人工神经网络模型。综上所述，测试数据最小的平均方差的神经网络拓扑结构为三层神经网络(输入层、隐层和输出层)，隐层节点数为8，tan-singmoid为隐层转移函数，pureline为输出层函数，人工神经网络结构如图4所示。

3.2 人工神经网络的预测结果

所建误差逆向传播人工神经网络的性能可以通过神经网络的输出值与实验所得结果的线性回归进行衡量和测试。神经网络通过数据训练初步成型，之后进行验证并加以调整，最后进行预测，图5所示为训练过程神经网络预测结果与实验所得实验结果的比较。

从图5中可以看出，误差逆向传播神经网络模型预测值与训练实验值的线性拟合度较高，斜率和相关系数分别为0.998和0.999，接近于1，说明模型的拟合极好。图6所示为神经网络预测值与验证实验结果之间的比较，斜率和相关系数分别为1.018和0.991，接近于1，表明该模型的预测较为可靠，可以用于臭氧协同氧化浸出反应过程中锑的浸出率预测。而图7所示为预测值与预测实验结果之间的比较，斜率和相关系数分别为0.976和0.997，说明所建误差逆向传播人工神经网络模型能够成功预测臭氧协同氧化浸出过程中不同条件下锑的浸出率，是一种具有参考价值和意义的模型。

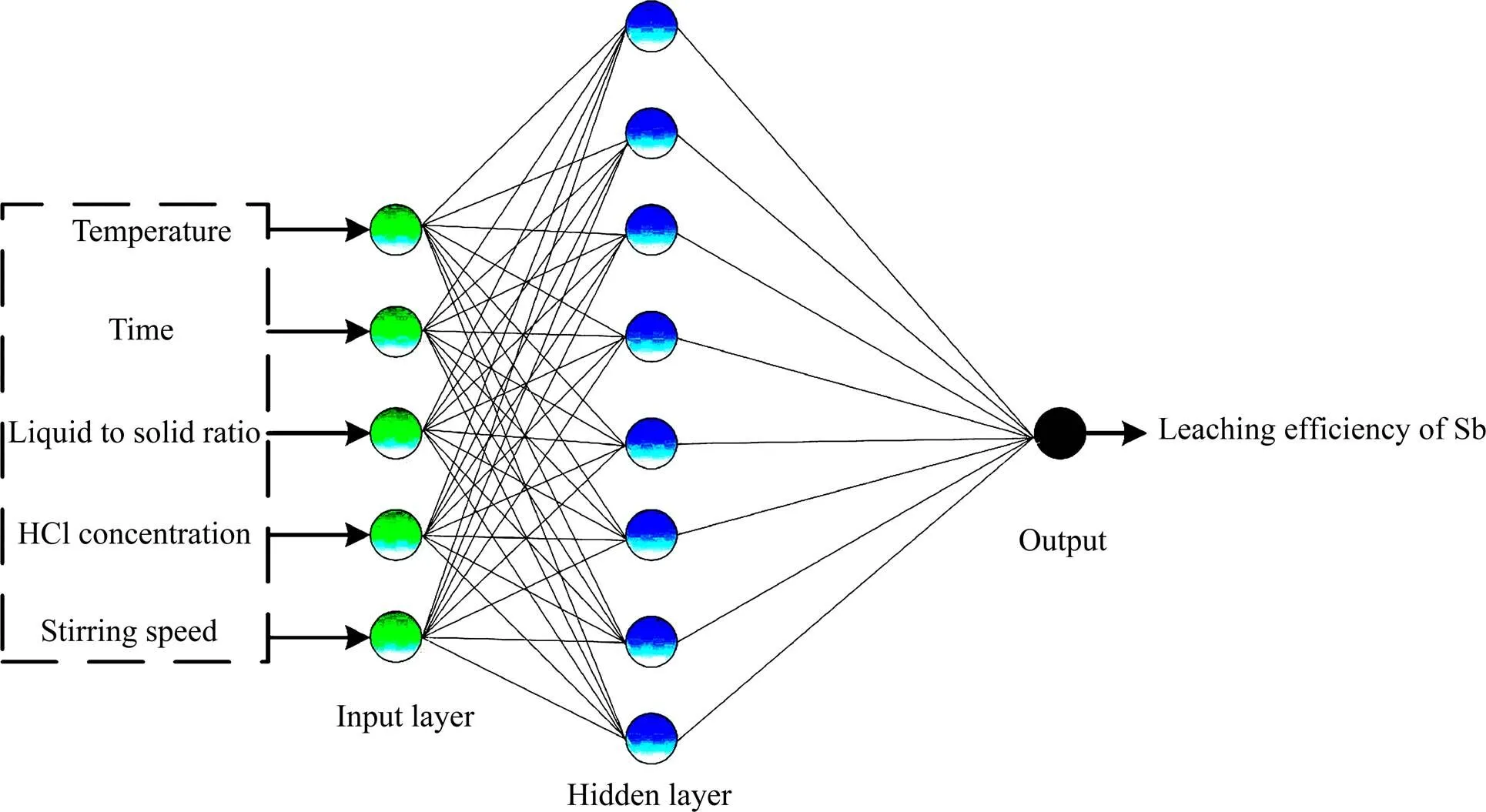
图4 最终神经网络结构图5-8-1型

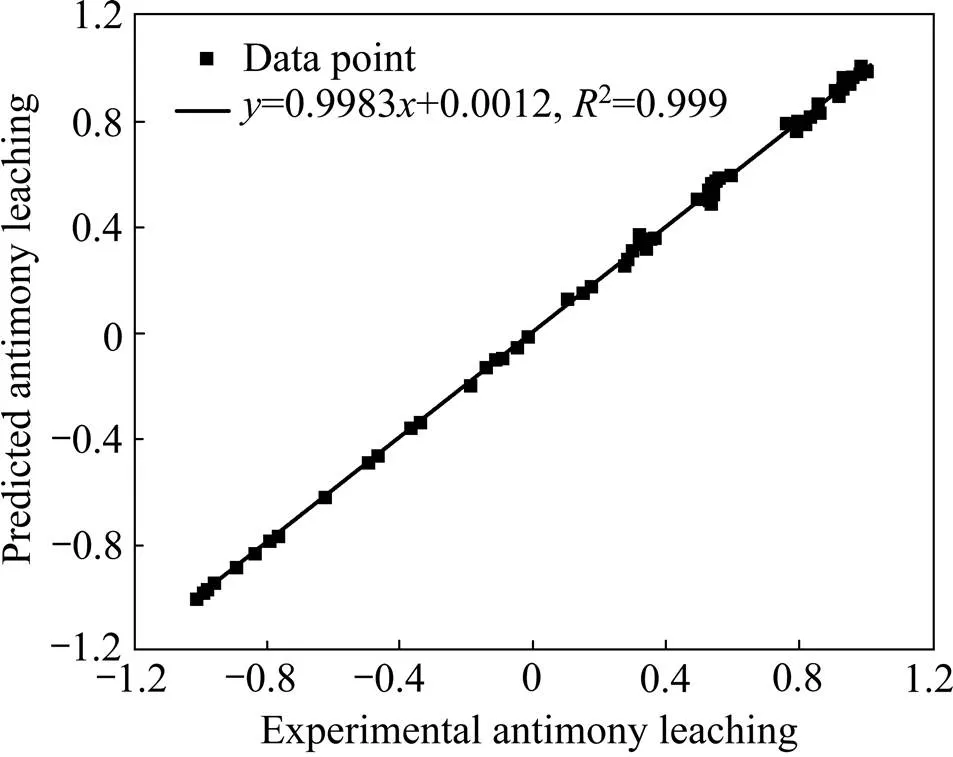
图5 锑浸出率训练集的奇偶校验

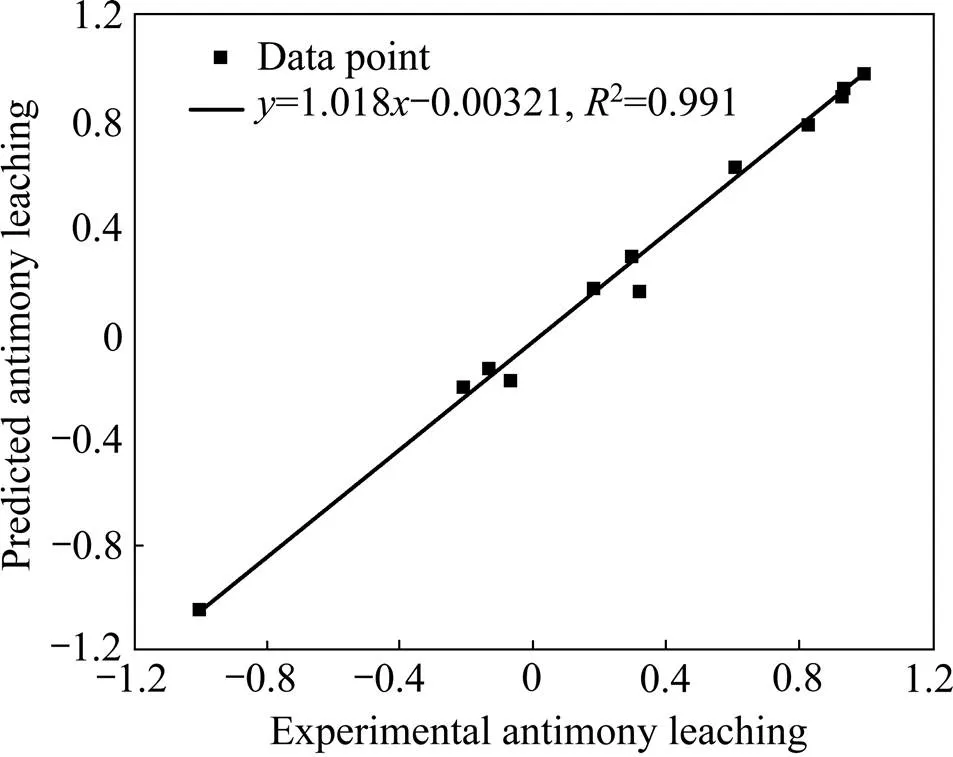
图6 锑浸出率验证集的奇偶校验

图7 锑浸出率预测集的奇偶校验

3.3 输入变量对锑浸出过程的影响作用

在人工神经网络中相互连接的节点之间的权重决定了其在该体系中的重要性和所占比例及影响，不同输入变量的相对重要性可以通过连接权重来衡量[25]，如式(6)所示。表4所列为相关层级之间的连接权重，其中1为反应温度，2为反应时间，3为液固比，4为搅拌速度，5为盐酸浓度。

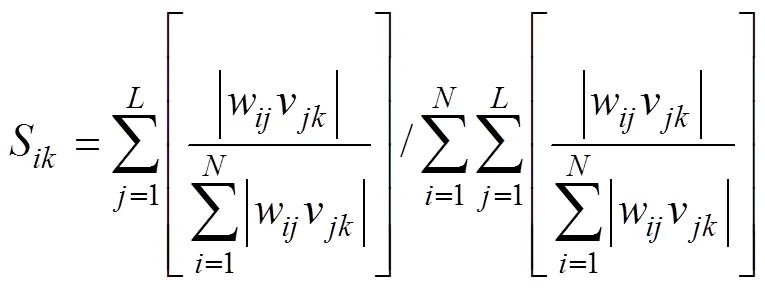
式中：为输入层节点数；为隐含层单元数；w代表输入层单元到隐含层的权重；v为隐含层节点数到输出层单元的权重；S为输入层单元到输出层单元的重要性。

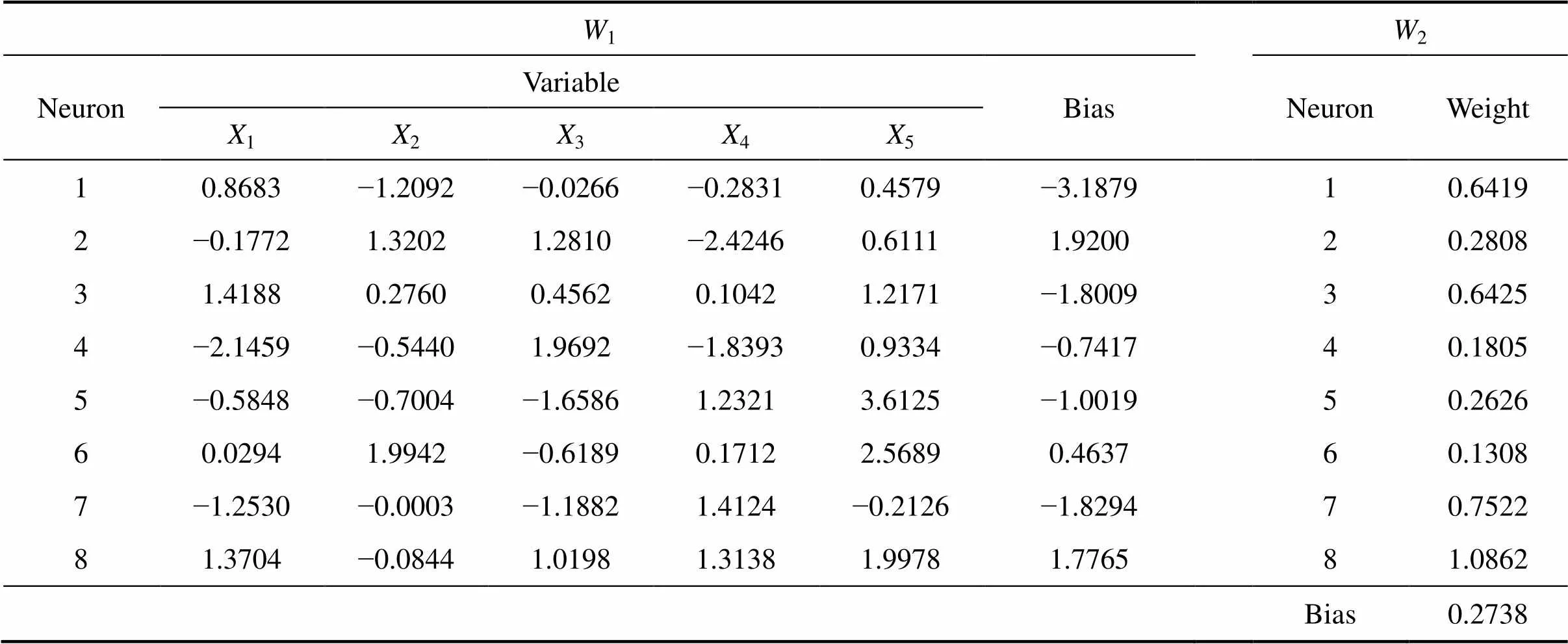
表4 相关层级的连接权重

根据式(4)~(13)可以计算出不同输入变量的相对重要性，结果如表5所列。从表5中可以看出，所有变量均对锑的浸出率有较大的影响，其重要性从高到低依次为：盐酸浓度、反应温度、搅拌速度、液固比、反应时间。盐酸浓度的影响主要体现在配位作用，这也与前面配位浸出实验结果相符。因此，选择反应条件时可以根据这一次序进行调整，选择更好的反应条件以达到更高的浸出效果。

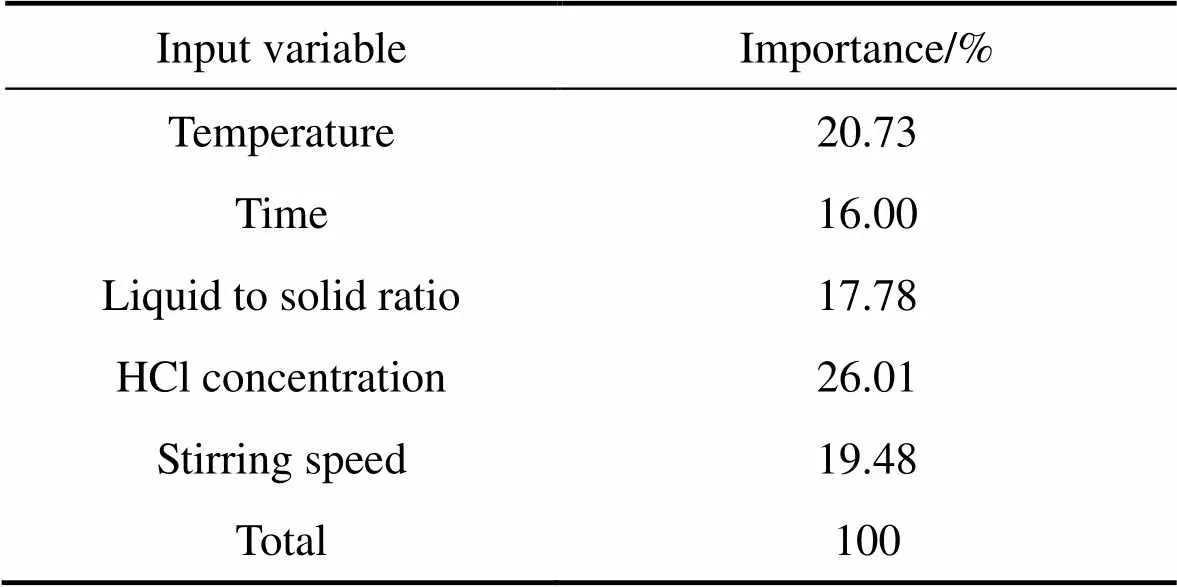
表5 不同输入变量的相对重要性

4 结论

1) 人工神经网络模型可以对臭氧协同氧化处理含锑硫化矿浸锑反应过程的实验值与预测值相关系数可达99%以上，线性拟合度较高，预测较为可靠，所建误差逆向传播人工神经网络模型能够成功预测臭氧协同氧化浸出过程中不同条件下锑的浸出率，是一种具有参考价值和意义的模型。

2) 采用人工神经网络模型对臭氧协同氧化浸锑过程进行模拟，建立起单隐层8节点的“5-8-1型”误差逆向传播神经网络模型，所建人工神经网络模型可以对反应过程做出有效的模拟和预测。

3) 根据所建神经网络模型中不同输入量在网络中节点权重不同，得出相关条件因素对锑浸出率的相对重要性从高到低依次为：盐酸浓度，反应温度，搅拌速度，液固比，反应时间。

[1] 赵天从. 锑[M]. 北京: 冶金工业出版社, 1987: 95−99. ZHAO Tian-cong. Antimony[M]. Beijing: Metallurgical Industry Press, 1987: 95−99.

[2] LIU Wei-feng, YANG Tian-zu, CHEN-Li, BIN Shu, BIN Wan-da. Development of antimony smelting technology in China[M]. 4th International Symposium on High-Temperature Metallurgical Processing. New York: John Wiley & Sons, Inc. 2013: 341−351.

[3] 徐康宁, 陈永明, 王岳俊, 薛浩天, 叶龙刚, 张文博. 辉锑矿铁源固硫还原熔炼直接炼锑[J]. 中国有色金属学报, 2017, 27(5): 1061−1067. XU Kang-ning, CHEN Yong-ming, WANG Yue-jun, XUE Hao-tian, YE Long-gang, ZHANG Wen-bo. Production of antimony by directly reducing-matting smelting of stibnite concentrate[J]. The Chinese Journal of Nonferrous Metals, 2017, 27(5): 1061−1067.

[4] RASCHMAN P, SMINCAKOVA E. Kinetics of leaching of stibnite by mixed Na2S and NaOH solutions[J]. Hydrometallurgy, 2012, 113/114(3): 60−66.

[5] UBALDINI S, VEGLIO F, FORNARI P, ABBRUZZESE C. Process flow-sheet for gold and antimony recovery from stibnite[J]. Hydrometallurgy, 2000, 57(3): 187−199.

[6] 赵瑞荣, 蒋汉瀛, 秦毅红. 我国湿法炼锑基础研究的现状与发展[C]// 中国有色金属学会. 全国第二届湿法冶金及第三届有色冶金物理化学学术会议论文集. 长沙: 中南大学, 1991: 669−678. ZHAO Rui-rong, JIANG Han-ying, QING Yi-hong. The present situation and development of basic research of wet smelting technology in China[C]//China Nonferrous Metals Society. Proceedings of the Second National Hydrometallurgy and the Third Nonferrous Metallurgical Physical Chemistry Conference. Changsha: Central South University, 1991: 669−678.

[7] 湛雪辉, 李朝辉, 湛含辉, 李 飞, 曹 芬, 李 侠. 臭氧−过氧化氢联合浸出方铅矿[J]. 中南大学学报(自然科学版), 2012, 43(5): 1651−1655. ZHAN Xue-hui, LI Zhao-hui, ZHAN Han-hui, LI Fei, CAO Fen, LI Xia. Combined leaching of galena by ozone-hydrogen peroxide solution[J]. Journal of Central South University (Science and Technology), 2012, 43(5): 1651−1655.

[8] AWE S A, KHOSHKHOO M, KRUGER P, SANDSTROM A. Modelling and process optimisation of antimony removal from a complex copper concentrate[J]. Transactions of Nonferrous Metals Society of China, 2012, 22(3): 675−685.

[9] CHEN Jing-lu, WANG Yong-jun, CHEN Yang. Research on stability of reverse unloading diaphragm pressure reducing regulator using BP neural network model[J]. Journal of Aerospace Power, 2013, 28(9): 2112−2120.

[10] MONIDEEPA M, SHIV B S. Artificial neural network: Some applications in physical metallurgy of steels[J]. Advanced Manufacturing Processes, 2009, 24(2): 198−208.

[11] WLAS M, KREMINSKI Z, GUZINSKI J, AUBRUB H, TOLIYAT H A. Artificial-neural-network-based sensorless nonlinear control of induction motors[J]. IEEE Transactions on Energy Conversion, 2005, 20(3): 520−528.

[12] LI Qing-cui, LI Deng-xin, CHEN Quan-yuan. Prediction of pre-oxidation efficiency of refractory gold concentrate by ozone in ferric sulfate solution using artificial neural networks[J]. Transactions of Nonferrous Metals Society of China, 2011, 21(2): 413−422.

[13] 毛 健, 赵红东, 姚婧婧. 人工神经网络的发展及应用[J]. 电子设计工程, 2011, 19(24): 62−65. MAO Jian, ZHAO Hong-dong, YAO Jing-jing. Development and application of artificial neural network[J]. Electronic Design Engineering, 2011, 19(24): 62−65.

[14] 汤素丽, 罗宇锋. 人工神经网络技术的发展与应用[J]. 电脑开发与应用, 2009, 22(10): 59−61. TANG Su-li, LUO Yu-feng. Development and application of artificial neural network technology[J]. Computer Development and Application, 2009, 22(10): 59−61.

[15] REN J P, SONG R G. Hardness prediction of 7003 aluminum alloy by gradient descent algorithm in BP artificial neural networks[J]. Advanced Materials Research, 2011, 217/218: 1458−1461.

[16] GHOSH A. Comparative study of financial time series prediction by artificial neural network with gradient descent learning[J]. Brain Broad Research in Artificial Intelligence & Neuroscience, 2013, 3(2): 26−30.

[17] 张 浩, 刘守城, 胡 义, 黄新杰, 任 崴. 基于正交设计与BP神经网络优化制备Cu-Ce/TiO2的预测模型[J].稀土, 2015, 36(2): 72−77. ZHANG Hao, LIU Shou-cheng, HU Yi, HUANG Xin-jie, REN Wai. Optimization of preparation of Cu-Ce/TiO2predictive model based on orthogonal design and BP neural network[J]. Chinese Rare Earths, 2015, 36(2): 72−77.

[18] HE Fei, He Dong-feng, XU An-jun, WANG Hong-bing, TIAN Nai-yuan. Hybrid model of molten steel temperature prediction based on ladle heat status and artificial neural network[J]. Journal of Iron and Steel Research (International), 2014, 21(2): 181−190.

[19] SU Xin, WU Ying-ya, PEI Hua-jian, GAO Jin-sen, LAN Xing-ying. Prediction of coke yield of FCC unit using different artificial neural network models[J]. China Petroleum Processing & Petrochemical Technology, 2016, 18(3): 102−109.

[20] KIM H J, JANG B S, PARK C K, BAE Y H. Fatigue analysis of floating wind turbine support structure applying modified stress transfer function by artificial neural network[J]. Ocean Engineering, 2018, 149: 113−126.

[21] 王 维, 李洪儒. BP神经网络在状态监测数据趋势预测中的应用[J]. 微计算机信息, 2005(21): 141−143. WANG Wei, LI Hong-ru. Application of BP neural network in trend forecasting of condition monitoring data[J]. Microcomputer Information, 2005(21): 141−143.

[22] 王 芳, 王明远, 马春旺, 王超群. 神经网络LM算法在X射线探测器中的应用[J]. 河南师范大学学报(自然版), 2013, 41(5): 39−41. WANG Fang, WANG Ming-yuan, MA Chun-wang, WANG Chao-qun. Application of neural network LM algorithm in X-ray detectors[J] Journal of Henan Normal University (Natural Edition) , 2013, 41(5): 39−41.

[23] MODARESI F, ARAGHINEJAD S, EBRAHIMI K. A comparative assessment of artificial neural network, generalized regression neural network, least-square support vector regression, and K-nearest neighbor regression for monthly stream flow forecasting in linear and nonlinear conditions[J]. Water Resources Management, 2018, 32(1): 1−16.

[24] 王用鑫. 煤矿设备中的基于动态模糊与BP神经网络的故障诊断[J]. 科技通报, 2016, 32(10): 195−198. WANG Yong-xin. Fault diagnosis based on dynamic fuzzy and BP neural network in coal mine equipment[J]. Science Bulletin, 2016, 32(10): 195−198.

[25] 皮钰鑫. BP人工神经网络在混凝土抗压强度预测中的应用[J]. 华东科技(学术版), 2017(8): 23−24. PI Yu-xin. Application of BP artificial neural network in prediction of concrete compressive strength[J]. East China Science and Technology (Academic Edition), 2017(8): 23−24.

Prediction for oxidation leaching behavior of antimony containing sulfide ore based on artificial neural network model

TIAN Qing-hua1, 2, 3, HONG Jian-bang1, XIN Yun-tao1, GUO Xue-yi1, 2, 3

(1. School of Metallurgy and Environment, Central South University, Changsha 410083, China; 2. Hunan Key Laboratory of Nonferrous Metal Resources Recycling, Changsha 410083, China; 3. Hunan Engineering Research Center of Nonferrous Metal Resources Recycling, Changsha 410083, China)

The leaching rate of antimony is an important index for the treatment of antimony sulfide ore. It is very important to obtain better leaching rate through conditional control in the process of oxidation leaching. In order to simulate and predict the oxidation leaching process of antimony containing sulfide ore, BP Neural network model was used to simulate the leaching process of antimony, and a 5-8-1 type model was established. The neural network model could predict the leaching efficiency of antimony in the process exactly, the correlation coefficient between experimental data and predicted data could reach 99%. According to the weights of inputs in the neural network model, the importances of different impacts are in the descending order: HCl concentration, temperature, stirring speed, liquid to solid ratio, time.

BP neural network model; leaching process of antimony; prediction; correlation coefficient; relative importance

Project(51474257) supported by the National Natural Science Foundation of China

2018-03-19;

2018-07-25

TIAN Qing-hua; Tel: +86-731-88877863; E-mail: qinghua@csu.edu.cn

国家自然科学基金资助项目(51474257)

2018-03-19；

2018-07-25

田庆华，教授，博士；电话：0731-88877863；E-mail: qinghua@csu.edu.cn

10.19476/j.ysxb.1004.0609.2018.10.18

1004-0609(2018)-10-2103-09

O639

A

(编辑 王 超)