巧用主元 事半功倍

安徽省枞阳县宏实中学(246700) 江保兵

一.一道竞赛试题和它的巧解

例1(1)求证：对于任意实数x,y,z,都有：.

这是2018年全国高中数学联赛安徽省初赛第11题,从公布的参考答案来看,本题主要考察基本不等式的应用,解题的关键在于相关系数的配凑.在教学中,笔者从另外一种角度入手,得到一个比较简单的解题方法.

证明这是一个二次结构,由于它对任意实数x恒成立,所以可以把它看作一个以x为主元的二次函数,利用判别式,我们得到：

这又是一个二次结构,由于它对任意实数y恒成立,所以可以把它看作一个以y为主元的二次函数,利用判别式,我们得到：

下面的两个例子的证明和例1的证明方法完全相同,读者不妨尝试一下.

(1)设α,β,γ为任意三角形的三个内角,x,y,z为任意实数.求证：x2+y2+z2≥ 2xycosα+2yzcosβ+2zxcosγ.

(2)(第2届陈省身杯数学奥林匹克第6题)对任意的x,y,z∈R,证明：.

我们看到转换思想,锁定主元,不仅解题方法直观简单,而且便于发散.本文再结合几道案例,进一步谈谈这种解题方法的应用.

二.解题方法的应用

例2(《数学通讯》(上半月)2018年第5期问题征解345题)已知正实数a,b,c,d,满足abcd=1,求证：.

解不妨设a≥b≥c≥d≥0,先固定b,c,构造以a为主元的函数.

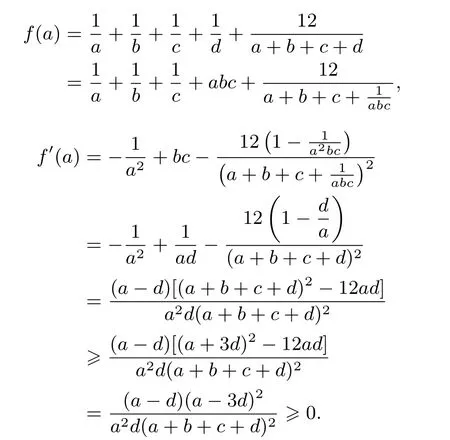
所以f(a)在区间[d,+∞)上单调递增,故f(a)≥f(d)=f(1)=7,当且仅当a=b=c=d=1时,等号成立.

下面式子的证明和例2的证明方法完全相同,读者不妨尝试一下.

数学的本质就是用数学的眼光认识世界,揭示数学规律,总结数学方法,形成数学思想.在平时的解题过程中,重视数学问题解法的追溯,刨跟问底,溯本求源,挖掘试题的数学本质,从中提炼出数学解题方法,这样才能知其然,更知其所以然.