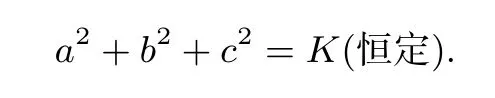双心圆彭赛列闭合三角形的六心线恒定不变性探讨
2018-11-16江苏省南京市东南大学211189徐文平
江苏省南京市东南大学(211189) 徐文平
一、引言
一个任意三角形必定有唯一的内切圆和外接圆,构成了三角形内切外接圆中圆问题,欧拉几何定理和彭赛列三角形闭合定理均是关于三角形内切外接双心圆的几何定理,联合分析二者几何特性能有什么新发现?当双心圆彭赛列三角形闭合变换时,有什么关键的点和线是永恒不变啊?
研究表明:欧拉几何定理的三角形内切外接圆中圆,三角形内切圆的切点三角形的垂心H,九点圆圆心V,重心G与原三角形内心I、外心O以及位似中心S六点共线,进一步研究表明:双心圆彭赛列三角形闭合变换时,六心线恒定不变(如图1),如此巧妙几何特性值得研究.
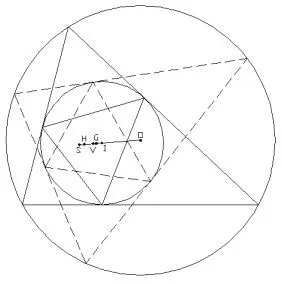
图1
二、切点三角形的六心共线性质简证
三角形内切圆的三个切点构成一个新三角形被定义为切点三角形,研究发现,三角形的切点三角形的垂心H,九点圆圆心V,重心G与原三角形内心I、外心O以及位似中心S六点共线.证明如下:
引理1(欧拉线)三角形的外心、重心、九点圆圆心、垂心,依次位于同一直线上,这条直线就叫三角形的欧拉线,且外心到重心的距离等于垂心到重心距离的一半.
引理2(垂足三角形的性质)锐角三角形的垂心H必为其垂足三角形的内心.
简证由赛瓦定理可知,AD、BE和CF交于垂心H.因为△DEF是垂足三角形,所以AB⊥CF,AC⊥BE,BC⊥AD.因为BCEF四点共圆,所以∠1=∠3;因为ABDE四点共圆,所以∠2=∠4.
因为∠3+∠B=90°,∠4+∠B=90°,所以∠3=∠4,所以∠1=∠2.因此,EB平分∠DEF,引理2成立.
引理3(旁心三角形的性质)三角形的旁心三角形垂心H是原三角形的内心.
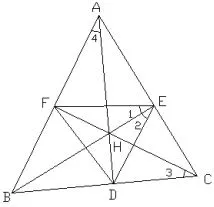
图2
简证如图2中,90°=∠1+∠AEF=∠3+∠B,所以∠AEF=∠B,90°=∠2+∠DEC=∠4+∠B,所以∠DEC=∠B=∠AEF.分析可知:因为AD平分∠EDF,AD与E、F两点外角平分线的交于A点,所以,A点为△DEF旁心圆的一个圆心.同理可知,B、C两点也是△DEF的旁心.因此,△ABC是△DEF是旁心三角形,H点是△ABC旁心三角形的垂心,又H点是△DEF原三角形的内心,引理3成立.
引理4(锐角三角形的位似关系循环定理)锐角三角形的切点三角形的垂足三角形与原有三角形位似;锐角三角形的垂足三角形的切点三角形与原有三角形位似.其位似关系性质可多重循环直至无穷,收敛于位似中心.
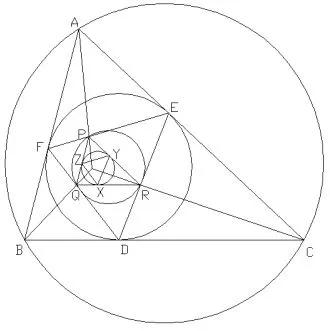
图3
简证△ABC内切圆三边的切点为D、E、F,△DEF为△ABC的切点三角形.△DEF三边的垂足为P、Q、R,△PQR为△DEF的垂足三角形.△PQR内切圆三边的切点为X、Y、Z,△XY Z为△PDR的切点三角形.依据引理 3,∠EDF=∠FPQ,∠EDF=∠EPR,依据切点三角形性质,∠EDF=∠AFE=∠AEF,所以,∠EDF=∠FPQ=∠EPR=∠AFE=∠AEF,∠QPR=180°-∠FPQ-∠EPR=180°-2∠EDF=∠A.
同理:∠PQR=∠B,∠PRQ=∠C,所以△PQR~△ABC,因为,∠FPQ=∠AFE,内错角相等,△PQR与△ABC的三条对应边平行,故△PQR~△ABC位似.锐角三角形的切点三角形的垂足三角形与原有三角形位似,证明成立.
同理可证:锐角三角形的垂足三角形的切点三角形与原有三角形位似.
分析可知,其位似关系性质可多重循环直至无穷,收敛于位似中心.
引理5(六心共线)三角形内切圆的切点三角形的垂心H,九点圆圆心V,重心G与原三角形内心I、外心O以及位似中心S六点共线.
传统的欧拉线是三角形的外心、重心、九点圆圆心、垂心,依次位于同一直线上,四心连线.分析三角形内切圆的切点三角形可知,切点三角形的垂心H,九点圆圆心V,重心G与原三角形内心I、外心O以及位似中心S六点共线.
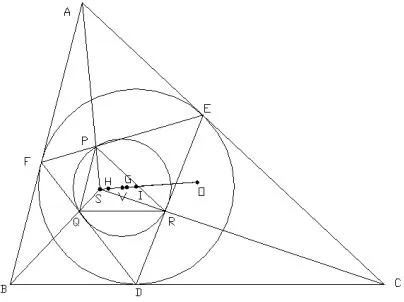
图4
简证如图4,△ABC是原三角形,△DEF是△ABC的切点三角形,△PQR是△DEF的垂足三角形.依据引理4,△PQR~△ABC位似,位似中心为S.因此,△ABC的外心O和△PQR的外心V以及位似中心S共线.(垂足三角形△PQR的外心V点就是切点三角形△DEF的九点圆圆心V点).
△PQR~△ABC位似,△ABC的内心I和△PQR的内心H以及S共线.(垂足△PQR的内心H就是切点三角形△DEF的垂心H).对于切点三角形△DEF,依据欧拉线,切点三角形的垂心H,九点圆圆心V、重心G与其外心I四点共线.(切点三角形△DEF的外心I就是原三角形△ABC的内心I).因此,切点三角形的垂心H,九点圆圆心V,重心G与原三角形内心I、外心O以及位似中心S六点共线.三角形内切圆的切点三角形的六心共线证明完毕.
三、双心圆彭赛列三角形闭合转换中六心线恒定不变性
研究表明:当双心圆作彭赛列三角形闭合变换时,其切点三角形的六心线恒定不变,在几何变换中发现了几何特性点不变的现象,具有研究意义.证明如下:
引理6外接椭圆的任意六点形,间隔连接顶点形成二个三角形,在椭圆内部可构成一个六边形,则内部六边形的三条对角线必定交于一点.
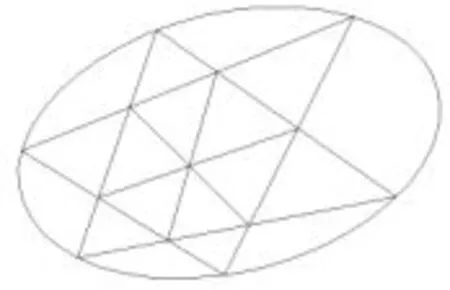
图5
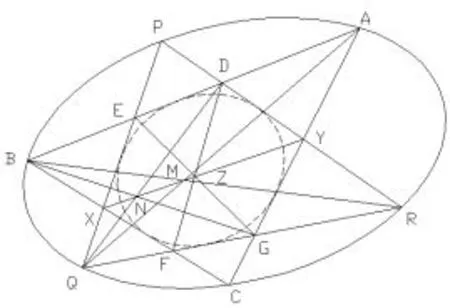
图6
简证如图6,依据帕斯卡定理,XMY三点共线.对BDA,QGR用帕普斯定理,有NMY共线,对BED,QFG用帕普斯定理,有XNZ共线.则XNMZY五点共线,即XZY三点共线,引理6成立.
引理7(彭赛列三角形闭合定理)对于双心椭圆K和C,假设存在一个内切外接双心圆的闭合三角形,则从外椭圆曲线K上任取一点P出发,内切外接双心圆K和C三次后一定能闭合,称为双心椭圆彭赛列闭合三角形.
简证布列安桑定理断言六条边和一条圆锥曲线相切的六边形的三条对角线共点,如图6,依据引理6和布列安桑定理,彭赛列闭合定理(N=3)成立.
引理8(欧拉几何定理)设三角形的外接圆半径为R,内切圆半径为r,外心与内心的距离为d,则有:d2=R2-2·r·R.

图7
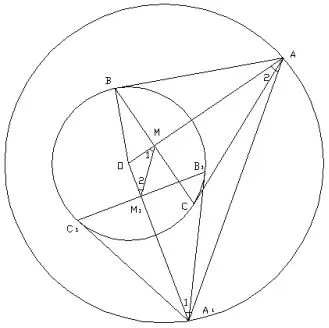
图8
引理9任意双心圆,小圆圆心为O点,在大圆上取二个点A和A1,过A点作小圆的切线交于B、C两个切点,过A1点作小圆的切线交于B1、C1两个切点,M为BC线段的中点,M1为B1C1线段的中点,则△OAA1~△OM1M.
证明如图8,假设小圆半径为r,依据射影定理可知:r2=OM·OA=OM1·OA1,则有:AA1MM1四点共圆,∠1=∠OMM1=∠OA1A;∠2=∠OM1M=∠OAA1,所以,△OAA1~△OM1M.
引理10(圆中圆定理)任意双心圆,在大圆上取一个动点A,作小圆的切线交于B、C两个切点,M为BC线段的中点,则M点的轨迹为一个圆.
简证一如图10,大圆上任意选取四点ABCD,做小圆切线,得到对应的极线中点A1B1C1D1四点.因为,ABCD四点共圆,即∠1+∠2+∠3+∠4=180°.依据引理9可知,分析A1B1C1D1四边形,对角之和为180°,所以,A1B1C1D1四点共圆.
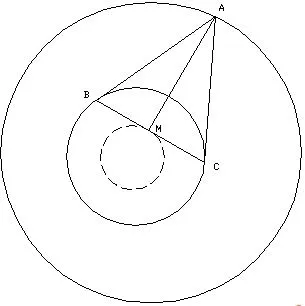
图9
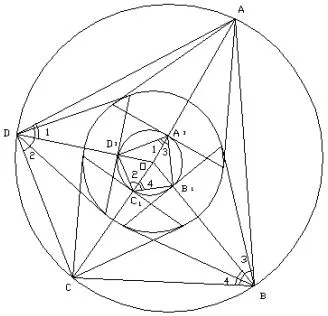
图10
简证二如图11,大圆上任意A,做小圆切线,得到对应的极线中点M点.A1A2在双心圆的两个圆心连线上,A1、A2二点相对应的极线中点为M1和M2点.依据引理9可知,∠M=∠1+∠2=90°,依据题意,M1和M2点是M轨迹两个圆心连线上的最左和最右端点.推理可知:M点的轨迹为一个圆,M1M2是M轨迹圆的直径.
引理11双心圆彭赛列三角形作闭合变换时,切点三角形的九点圆恒定不变.
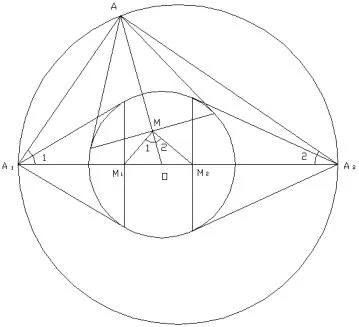
图11
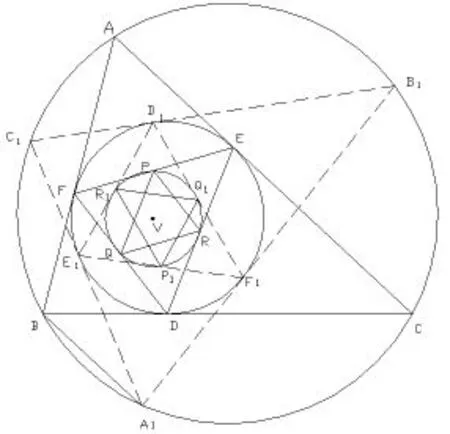
图12
简证如图12,彭赛列三角形△ABC闭合变换为三角形△A1B1C1,相应的切点三角形△DEF变换为切点三角形△D1E1F1,切点三角形的中位线三角形△PQR变换为中位线三角形△P1Q1R1.PQRP1Q1R1六点均是切线极线的中点,依据引理9可知,PQRP1Q1R1六点共圆于圆V.依据九点圆定义,切点三角形△DEF和切点三角形△D1E1F1具有相同的九点圆.因此,双心圆彭赛列三角形作闭合变换时,切点三角形的九点圆恒定不变.
定理12(六心连线不变性)双心圆彭赛列三角形作闭合变换时,切点三角形的垂心H,九点圆圆心V,重心G与原三角形内心I、外心O以及位似中心S六点共线,六心线恒定不变.
简证如图13,在双心圆中,△ABC彭赛列三角形闭合变换到△A1B1C1的位置.△ABC的切点三角形为△DEF,△DEF的垂足三角形为△PQR.△A1B1C1的切点三角形为△D1E1F1,△D1E1F1的垂足三角形为△P1Q1R1.△PQR和△P1Q1R1的外接圆分别是△DEF和△D1E1F1的九点圆.
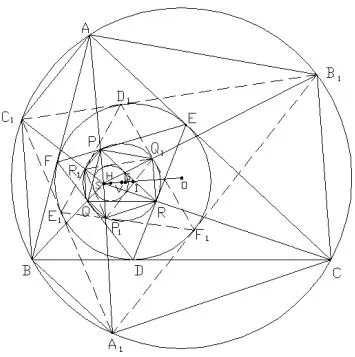
图13
依据引理 11可知,切点三角形△DEF和切点三角形△D1E1F1具有相同的九点圆.因此,△PQR和△P1Q1R1具有相同外接圆,圆心V相同.双心圆彭赛列三角形闭合变换时,△DEF和△D1E1F1切点三角形的九点圆圆心V位置不变,半径均为圆I半径的一半.因为,切点三角形为△DEF和切点三角形△D1E1F1的二组六心线中,其中三点是恒定不变(九点圆圆心V、原三角形内心I、外心O在命题中是固定的).
因为,切点三角形的九点圆圆心V,重心G,垂心H,外心I四点共线,且HG=2IG,IG=2V G,IH=2IV,这些点互相之间比例关系恒定的.因此,双心圆彭赛列三角形闭合变换时,切点三角形的九点圆心V和外心I恒定不变,所以,重心G,垂心H也恒定不变.所以,切点三角形为△DEF和△D1E1F1二组六心线中五点完全重合,五心恒定不变(九点圆圆心V,重心G,垂心H和原三角形内心I、外心O).因为,△PQR和△P1Q1R1的外接圆相同,六点共圆.又依据引理4可知,△ABC与△PQR位似,△A1B1C1与△P1Q1R1位似,二者位似比相同.所以,六边形ABCA1B1C1与六边形PQRP1Q1R1位似.因此,双心圆彭赛列三角形闭合变换时,△ABC与△PQR位似关系转变成为△A1B1C1与△P1Q1R1位似,二者的位似中心S点相同.定理12证明完毕.
三、彭赛列双心圆切点三角形的六心位置
双心圆彭赛列三角形闭合变换时,切点三角形的垂心H,九点圆圆心V,重心G与原三角形内心I、外心O以及位似中心S六点共线,且方向和位置恒定不变.在几何变换中发现了几何特性点不变的现象,具有重要研究意义.
彭赛列三角形闭合特性是仅仅取决于彭赛列双心圆,即取决于双心圆大圆半径R、小圆半径r,因此,六心之间的距离也仅仅取决于彭赛列双心圆的半径r、R两个参数.
1.双心圆圆心距离d
依据欧拉几何定理:d2=R2-2·r·R=f1(r,R).式中的d为三角形大圆圆心O和小圆圆心I之间的距离.
2.九点圆圆心V,垂心H和重心G的位置
九点圆半径为三角形外接圆半径的一半,如图14,,依据引理11的简证方法二得.依据射影定理,
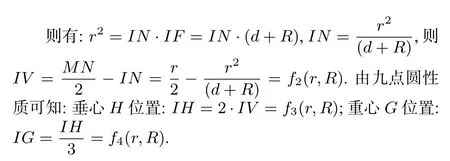
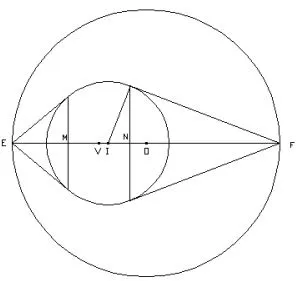
图14
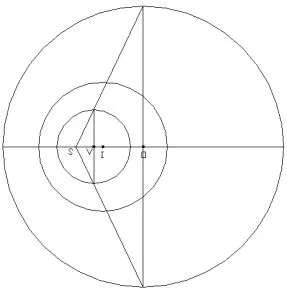
图15
3.位似中心S的位置
如图15,双心圆彭赛列三角形闭合变换时,所有切点三角形的九点圆相同,九点圆和大圆的位似中心S点,就是双心圆彭赛列三角形闭合变换时所有位似三角形的位似中心S点.假设距离IS为x,则,整理得:.
4.思考
1)彭色列三角形闭合变换时,原三角形的旁心也在六心线上.
2)彭色列三角形闭合变换时,所有切点三角形的三条边长的平方之和是恒定不变,即