解析文科数学全国卷中的线性规划问题

广东省东莞市第二高级中学(523129) 章锐阳

简单线性规划是新课程高中数学必修五第三章的内容.自从简单线性规划问题进入高考,简单线性规划已是高考的必考内容.它以目标函数的最值为重点,兼顾考查代数式的几何意义(如截距、斜率、距离、面积等),简单线性规划是沟通几何知识与代数知识的重要桥梁,是数形结合的集中体现,体现了高中数学常用的数学思想,如数形结合思想,转化与化归思想,而且还能体现学生综合分析问题的能力及解决实际问题的能力.

1.用图形法求解简单线性规划问题的步骤

图形法不仅直观,而且可从中得到有关简单线性规划问题的一些做题结论.图形法要求是：在平面上画出可行域,画出目标函数的等值线,将目标函数的等值线平移得到最优解.图形法的步骤为：

①建立平面直角坐标系;

②画图表示简单线性规划问题的约束条件,画出简单线性规划问题的可行域;

③画出目标函数z=ax+by的平行线ax+by=0;

④画图表示目标函数的等值线束(注意等值线束必须在可行域内);

⑤根据所求最值问题,将目标函数的等值线束保持与ax+by=0平行地平移,直到再继续移动就与可行域不相交时为止,此时该目标函数直线与可行域的交点即为最优解.

2.简单线性规划的题型

每年的文科数学全国卷总有一个简单线性规划问题,近八年来5次与目标函数最大值有关,2次与目标函数最小值有关,1次求与目标函数范围(最小值和最大值),大致可以分为以下四个类型.

2.1 已知线性约束条件,求线性目标函数最值

线性约束条件明确的简单线性规划题

目是最基本、最常见的类型,也是考生最容易得分的题目.只要准确画出可行域,问题就迎刃而解.下面列举了五年的文科数学全国卷真题,题目浅显易懂,做法简单.

题目1(2018年全国卷文科第14题)设x,y满足约束条则z=3x+2y的最大值为___.

题目2(2017年全国卷文科第7题)设x,y满足约束条则z=x+y的最大值为()

A.0 B.1 C.2 D.3

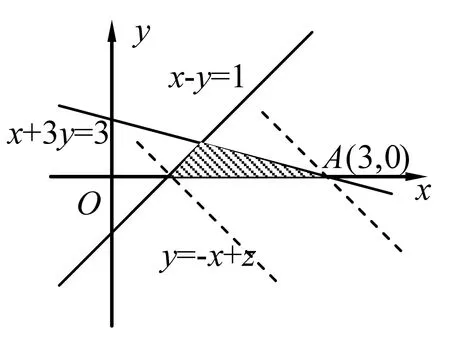
图1

图2

解如图1,目标函数z=x+y经过A(3,0)时最大,故zmax=3+0=3,故选D.

题目3(2015年全国卷文科第15题)若x,y满足约束条则z=3x+y的最大值为___.

解作出可行域△ABC,如图2.画出直线l0:3x+y=0,平移l0到l,当l经过点A时z最大,联立x+y-2=0与x-2y+2=0,解得交点A(1,1),所以zmax=4.

题目4(2013年全卷文科第14题)设x,y满足约束条件则z=2x-y的最大值为___.

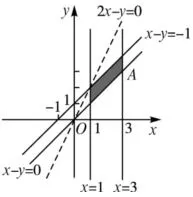
图3

图4

解析画出可行域如图3所示.画出直线2x-y=0,并平移,当直线经过点A(3,3)时,z取最大值,且最大值为z=2×3-3=3.

题目5(2011年全国卷文科第14题)若变量x,y满足约束条件则z=x+2y的最小值为____.

解析在坐标系中画出可行域,如下图4.可知当直线过点A时取得最小值,由,可得A的坐标为(4,-5),故z=x+2y的最小值为-6.故答案为-6.

从以上几年的高考真题中可以看出简单线性规划考题以填空题为主,题意简明易懂,都是直接给出线性约束条件和线性目标函数,考生只要根据线性约束条件准确地画出可行域,然后根据图形法求解,求解过程对考生要求更细心、准确.

2.2 寻找线性约束条件,求应用问题最值

在解决线性规划实际应用问题时,审题是关键.需要通过审题理解题意,找出各个量之间的关系,有时先列成表格,找出线性约束条件,写出所研究的目标函数,转化为简单的线性规划问题,再按照图形法完成求解.

题目6(2011年全国卷文科第16题)某高科技企业生产产品A和产品B需要甲、乙两种新型材料.生产一件产品A需要甲材料1.5kg,乙材料1kg,用5个工时;生产一件产品B需要甲材料0.5kg,乙材料0.3kg,用3个工时.生产一件产品A的利润为2100元,生产一件产品B的利润为900元.该企业现有甲材料150kg,乙材料90kg,则在不超过600个工时的条件下,生产产品A、产品B的利润之和的最大值为____元.

图5

解析设生产产品A,B的件数分别为x,y,获得利润为z元,则x,y满足约束条件为：目标函数为z=2100x+900y=300(7x+3y),画出满足不等式组的可行域,如图5所示.联立得即A(60,100).移动目标函数,可得到当其经过点A(60,100)时,z有最大值216000.故填216000.

解线性规划应用题时有三个注意点：①明确问题中的所有约束条件,并根据题意判断约束条件是否能够取得等号.②注意结合实际问题的实际意义,判断所设未知数x,y的取值范围,特别注意分析x,y是否为整数、是否为非负数等.③正确地写出目标函数,一般地,目标函数是等式的形式.

2.3 综合性强,隐蔽性较深的线性规划问题

题目隐含简单线性规划问题,题型灵活多变,在求解题目时必须把握问题的本质,进行分析与转化处理.通过直角坐标系,利用点的坐标确定可行域,然后利用图形法求解,求解过程要求考生更为细心、准确.

题目7(2012年全国卷文科第5题)已知正三角形ABC的顶点A(1,1),B(1,3),顶点在第一象限,若点(x,y)在△ABC内部,则z=-x+y的取值范围是()

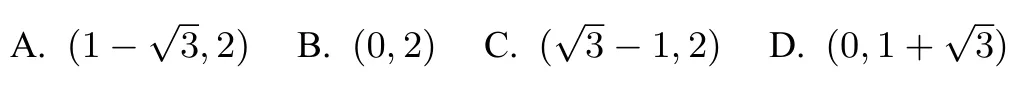
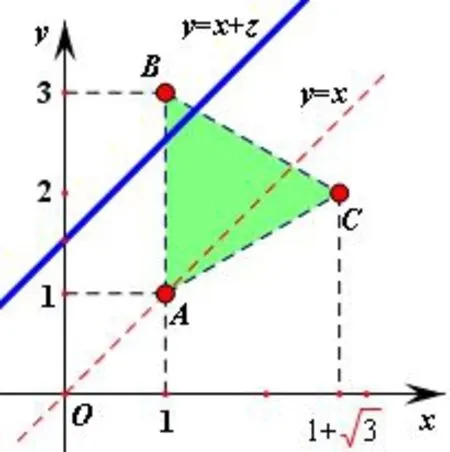
图6

解析正△ABC内部如图6所示,A(1,1),B(1,3),C(1+.将目标函数z=-x+y化为y=x+z,显然在B(1,3)处,zmax=-1+3=2;在C(1+因为区域不包括端点,所以,故选择A.

2.4 含参数的简单线性规划问题

线性规划问题参数可以分为三种不同类型：线性约束条件定,目标函数含参数;线性约束条件含参数,目标函数定;线性约束条件含参数,目标函数含参数.八年来唯一一次考查了含参数的简单线性规划问题,但是难度不大.

题目8(2014年全国卷文科第11题)设x,y满足约束条件且z=x+ay的最小值为7,则a=()

A.-5 B.3 C.-5或3 D.5或-3

解联立x+y=a与x-y=-1解得交点,z取得最值,解之得a=-5或a=3.但a=-5时,z取得最大值,舍去,所以a=3,故选B.

简单解决这类问题时,首先要注意对参数取值的讨论,以确定符合题意的可行域,寻找最优解,从而确定参数的值.

3.备考策略

简单线性规划问题是在线性约束条件,线性约束目标函数的情况下的一类最优解问题.在约束条件是线性的情况下,线性目标函数只有在可行域的顶点或者边界上取得最值,在做选择题或者填空题时,可以根据可行域的顶点直接进行检验求解,最大的检验结果为最大值,最小的检验结果为最小值.对于文科数学来讲,八年来全国卷线性规划问题考查的本质内容基本一致,都可以直接用可行域的顶点直接检验求解.因此我们在备考的时候,主流方向是教授图形法解决简单线性规划问题,但对于一些实在无法理解目标函数的等值线束的考生来说,我们就必须对他们训练顶点检验法,提高他们的得分能力.

考生应该做到：对于常考形式必须滚瓜烂熟,对于不常见的形式也必须知晓.因此相关非线性问题的问题求解也要清楚.对于给定平面区域求解一些非线性目标的最值或范围时,要根据解析几何知识理解目标的几何意义,根据几何知识解决问题,有时需要适当变换求解目标的形式,使得几何意义更加确定,便于问题的解决.常见代数式的几何意义主要有：表示点(x,y)与原点(0,0)的距离,表示点(x,y)与点(a,b)的距离.②表示点(x,y)与原点(0,0)连线的斜率,表示点(x,y)与点(a,b)连线的斜率.

总之,利用简单线性规划的图形法,可以提高学生综合分析问题的能力,逻辑思维能力以及运用数学知识解决实际问题的能力.本文从图形法解简单线性规划问题出发,将不等式作为解决优化问题的工具,用不等式组刻画平面区域,借助几何直观解决一些简单线性规划问题,有助于学生进一步体会优化思想,理解数形结合的方法以及不等式在解决与实际情境相关的优化问题中的工具作用.