高速车辆抗蛇行减振器可切换模糊控制研究
2018-11-15刘志明金天贺
张 坤, 刘志明, 金天贺
(北京交通大学 机械与电子控制工程学院, 北京 100044)
随着生活品质的提高,人们对列车运行速度的要求越来越高。但行驶速度的提高会受到蛇行临界速度的限制,所以高速车辆在二系悬挂中装有抗蛇行减振器。要提高列车的临界速度,就需要合理地增大抗蛇行减振器阻尼,但纵向阻尼力过大,会影响列车曲线通过的安全性。因此,横向稳定性和曲线通过性能之间的矛盾是车辆提速过程中亟待解决的问题之一[1-2]。如何通过控制抗蛇行减振器阻尼来解决此矛盾,是文中的主要研究内容。
现有研究大都通过改变车体、转向架等结构形式或者对悬挂参数进行优化,来协调横向稳定性与曲线通过性能[3-7]。抗蛇行减振器的研究主要集中在减振器参数优化、对车辆性能的影响等方面,如文献[8]对阻尼系数和节点刚度等参数进行了优化分析,文献[9]研究了抗蛇行减振器主要参数对车辆动力学性能的影响。上述方法虽然可以提高车辆整体动力学性能,但并不能彻底解决横向稳定性和曲线通过性能之间的矛盾。
文中基于某型磁流变减振器结构[10],提出一种抗蛇行减振器可切换模糊半主动控制模型,使抗蛇行减振器在直线和曲线轨道运行时分别在两个不同的阻尼范围内变化。在直线轨道运行时,抗蛇行减振器阻尼力较大,保证车辆的横向稳定性;在曲线轨道运行时,其阻尼力切换成较小值,以保证车辆具有较高的安全通过曲线性能。与传统的阻尼特性固定模式不同,可切换模糊控制可以根据线路几何状况来调整阻尼参数,并通过SIMPACK-Matlab联合仿真验证在高速车辆抗蛇行减振器中应用此半主动控制方法的控制效果。
1 高速车辆动力学模型的建立
1.1 车辆系统模型
文中建立的某型高速列车的车辆动力学模型由4条轮对、8个轴箱转臂、2个构架和1个车体组成,模型中还有牵引拉杆、横向止挡、抗侧滚扭杆,共50个自由度。该系统50个自由度的运动微分方程组可写成矩阵形式[11]:
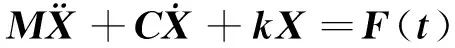
(1)
车轮采用的是S1002磨耗型型面,线路钢轨轨廓为UIC60型。动车组悬挂系统中的二系横向减振器以及抗蛇行减振器的阻尼力与其两端相对运动速度之间呈一定的非线性关系,减振器阻尼特性非线性关系如表1所示。

表1 车辆减振器非线性参数
用SIMPACK软件建立车辆动力学模型,如图1所示。
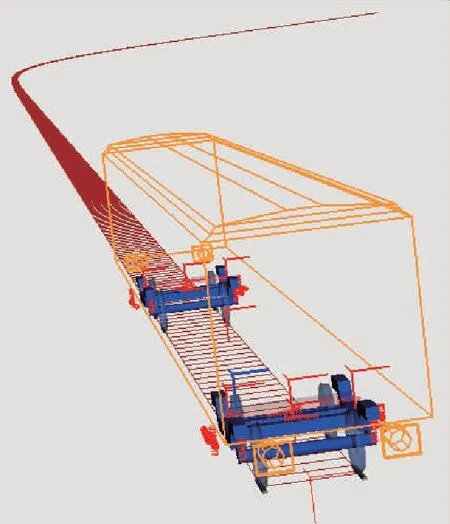
图1 车辆动力学模型
1.2 轨道几何参数
轨道不平顺激励对于车辆系统作为一种激励函数输入,它使得车辆系统产生各种强迫振动,这些振动对车辆动力学会造成重要影响。仿真模型中轨道的组成为200 m直线、500 m缓和曲线、1 000 m圆曲线、500 m缓和曲线与200 m直线。整体为一条完整线路,曲线半径为7 000 m,曲线超高150 mm。采用京津线实测的线路不平顺。
1.3车辆动力学模型的验证
车辆系统动力学模型建立后需验证其正确性,车辆以300 km/h在京津线轨道激励上匀速运行时车体和构架垂向振动加速度时间历程如图2,可得构架垂向振动加速度最大值为3.36 m/s2,车体垂向振动加速度最大值为0.37 m/s2,与线路实测高速车辆车体和构架垂向振动加速度最大值数量级一致。
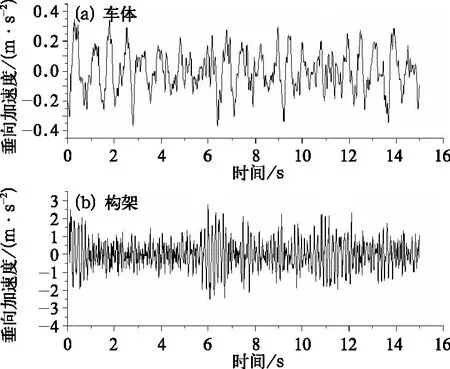
图2 构架及车体振动加速度时域图
计算得到车辆非线性临界速度为515 km/h,远超过实际最高运行速度350 km/h。
2 可切换模糊半主动控制
2.1 控制算法切换指标
为使车辆在直线与曲线轨道上同时获得良好的动力学性能,抗蛇行减振器阻尼需要在两种不同的阻尼特性之间进行切换以适应不同运行工况的需要。因此,需要设置合理的指标,实现直线、曲线轨道的判断。车辆通过曲线轨道时,由于轨道存在超高,车体发生倾斜,垂向位移会发生变化。文中选取车体质心垂向位移作为判断指标,采用所建的车辆动力学模型,模拟运行速度300 km/h,分别通过直线轨道和曲线轨道,轨道施加实测不平顺激励,仿真可得车体质心垂向位移如图3所示。由图可得,车体质心垂向位移在直线轨道和曲线轨道相差高达70 mm,证明所选取的指标是可行的;由仿真结果选取直线轨道与曲线轨道间切换值为20 mm。
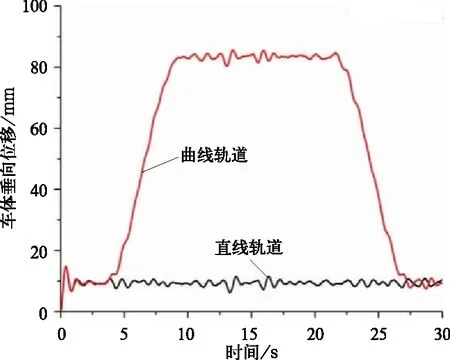
图3 直线与曲线轨道车体质心垂向位移
2.2 切换控制器设计
车辆在直线轨道运行时,临界速度越高表示车辆的横向稳定性冗余越充足。曲线通过时,脱轨系数的大小可以表征车辆运行的安全性,脱轨系数越小,曲线通过的安全性越高。
为了分析抗蛇行减振器阻尼特性对车辆运行横向平稳性与曲线通过性能的影响,以车辆选用的某抗蛇行减振器阻尼参数为基准,选取0.5倍至2.5倍的标准抗蛇行减振器阻尼作为阻尼参数波动范围,如图4所示。仿真计算车辆运行速度为300 km/h,线路施加实测不平顺激励,得到直线轨道的临界速度和曲线轨道的最大脱轨系数分别如图5和图6。
由图5可得,车辆在直线运行时,抗蛇行减振器阻尼越大,临界速度越大,即横向稳定性越好,但抗蛇行减振器阻尼力不能无限大,考虑到技术限制,在直线轨道运行时抗蛇行减振器饱和阻尼力取42.5 kN。由图6可得,车辆在曲线运行时,0.9倍标准抗蛇行减振器阻尼的脱轨系数最小,因此选取饱和阻尼力为15.3 kN作为曲线通过时的抗蛇行减振器饱和阻尼力。即可切换控制表达式如下:
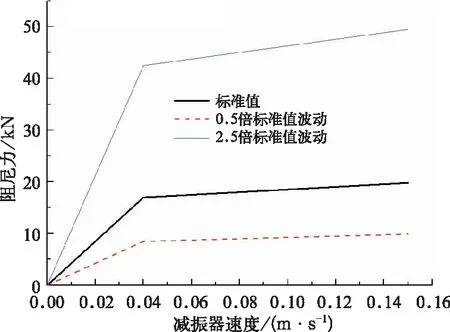
图4 抗蛇行减振器阻尼特性曲线
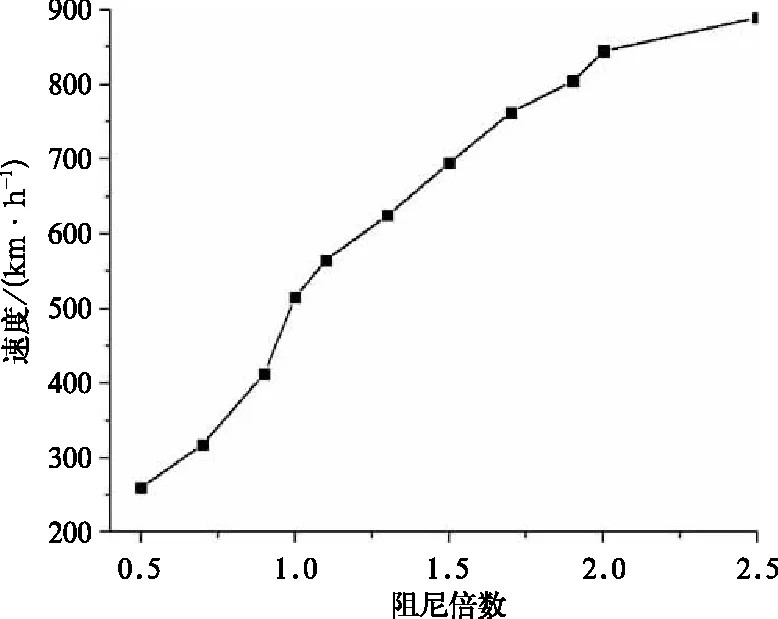
图5 非线性临界速度随阻尼力的变化
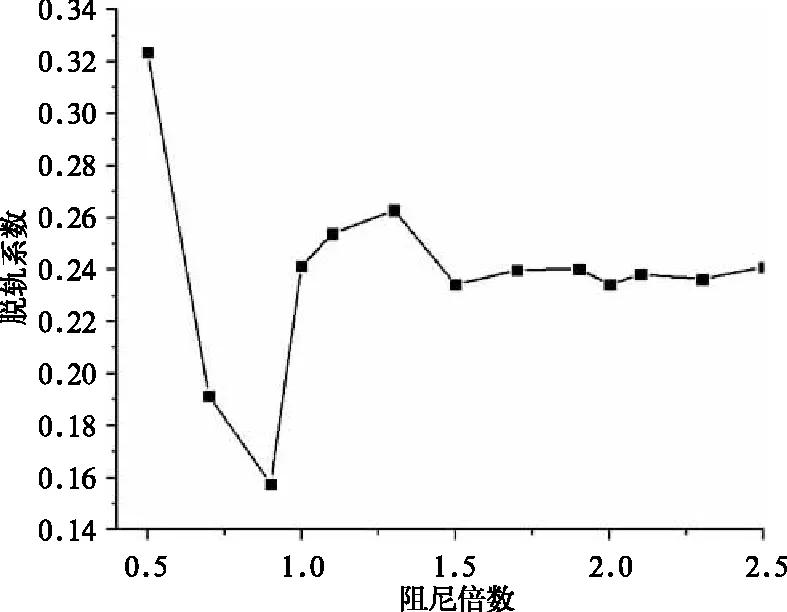
图6 脱轨系数随阻尼力的变化

(2)
式中,F为抗蛇行减振器饱和阻尼力;Δz为车体质心垂向位移。
可切换控制中,直线和曲线轨道运行时,抗蛇行减振器都是固定的阻尼特性,只有在特定运行条件下,动力学性能才能达到最优,不能随路况及车辆实时运行状态调整其阻尼特性。针对此问题,文中在直线和曲线轨道上分别采用模糊控制方法。
2.3 模糊控制器设计
根据车体质心垂向位移判断出的线路状况,分别对曲线与直线运行工况进行模糊控制。由于抗蛇行减振器卸荷后,阻尼系数较小,故只对工作区进行模糊控制。
根据抗蛇行减振器作用原理,选择减振器活塞相对速度与理想值的偏差以及偏差变化率作为模糊控制输入变量,减振器阻尼力为模糊控制器输出量。设偏差为E,偏差变化率为EC,输出抗蛇行减振器阻尼力为U。
模糊语言变量E的语言值设为9个,即{NB,NM,NS,NW,Z,PW,PS,PM,PB},模糊论域选为[-4,4],确定比例因子为10;偏差变化率的模糊语言变量EC的语言值设定为7个,即{NB,NM,NS,Z,PS,PM,PB},模糊论域选为[-4,4],确定比例因子为2;输出模糊语言变量U的语言值设定为9个,即{NB,NM,NS,NW,Z,PW,PS,PM,PB},模糊论域选为[-500,500],根据式(2)可以得出,车辆在直线轨道和曲线轨道运行时,抗蛇行减振器阻尼力不同,确定车辆在直线轨道运行时,比例因子为85,曲线轨道运行时,比例因子为30。
模糊控制输入输出变量的隶属度函数选用三角函数,模糊推理方法采用Mamdani方法,解模糊法为面积重心法,推理为max-min方法。
模糊规则确定的原则是:当抗蛇行减振器活塞相对速度为负大时,若其变化率为负,即速度有负向增大的趋势,为尽快减小已有速度值,并抑制速度的增大,减振器阻尼力应取负大;当速度为负中时且变化率为正时,系统本身已具有减小速度的趋势,所以为了尽快减小速度而又不超调,减振器阻尼力取负小;当速度为负小,系统接近稳态,若变化率为负时,为了抑制速度继续增大,减振器阻尼力应取负小。当抗蛇行减振器活塞相对速度为正值时,同理进行设置。具体的模糊规则如表2所示。
3 联合仿真结果及分析
在MATLAB/Simulink中建立抗蛇行减振器的控制模型,与上面SIMPACK中建立的车辆动力学模型,通过SIMAT接口进行数据传递,实现联合仿真。联合仿真集合了SIMPACK和MATLAB软件各自的优势,可以解决复杂的整车模型和控制器仿真。SIMPACK模型输出信号为4个抗蛇行减振器活塞速度及车内地板中心垂向位移,输入信号为MATLAB控制器计算得到的抗蛇行减振器阻尼力,联合仿真模型如图7所示。
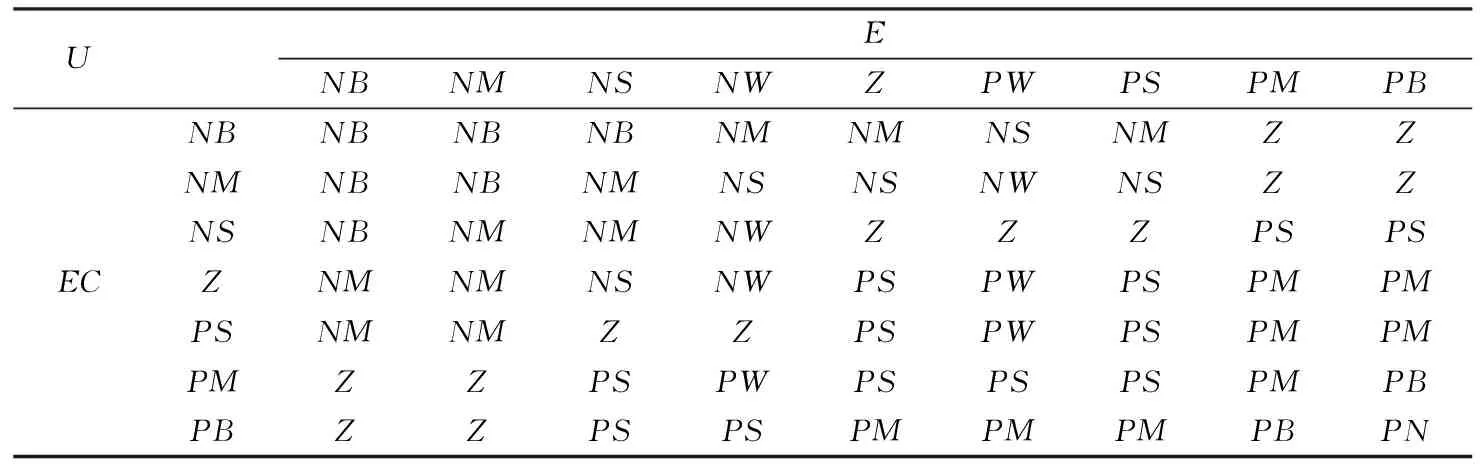
表2 模糊控制规则
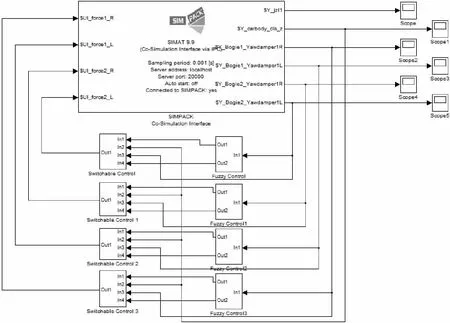
图7 可切换模糊控制联合仿真模型
为了考察可切换模糊半主动控制的效果,按照所建模型中设置的曲线轨道和直线轨道,施加线路实测不平顺激励,模拟运行速度300 km/h,仿真计算车辆直线运行和曲线运行工况下的相关动力学性能指标。
3.1 直线工况分析
由SIMPACK-Matlab联合仿真计算高速车辆在可切换控制和可切换模糊控制下的非线性临界速度,如图8所示,由图可得,与被动控制相比,切换控制临界速度由515 km/h提高到890 km/h,增幅为72.8%。可切换模糊控制临界速度由515 km/h提高到940 km/h,增幅高达82.5%,由此可得可切换模糊控制相对于被动控制抗蛇行减振器,车辆的横向稳定性和非线性临界速度得到了很大提高,且优于可切换控制模型。
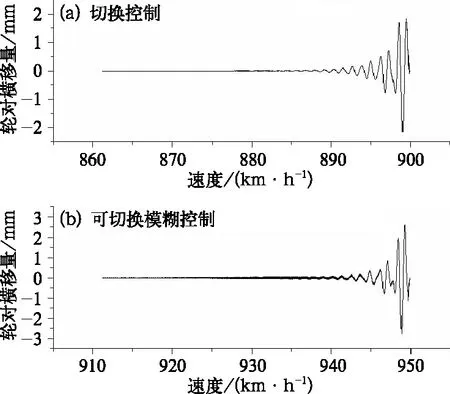
图8 半主动控制控制下车辆临界速度
3.2 曲线工况分析
仿真计算抗蛇行减振器在被动控制、可切换控制和可切换模糊控制下的车辆脱轨系数、轮重减载率、轮轨横向力和磨耗指数如图9~图12所示。
由图9~图12可以得到,切换控制下的曲线通过性能有所提高,脱轨系数由0.24降至0.15,降幅37.5%,轮重减载率由0.45降至0.44,降低2.2%,轮轨横向力由7.85 kN降至6.07 kN,降幅22.7%,磨耗指数由6.65降至6.08,降幅为8.6%;在可切换模糊控制下的曲线通过性能进一步提高,脱轨系数由0.24降至0.12,降幅50.0%,轮重减载率由0.45降至0.43,降幅为4.4%,轮轨横向力由7.85 kN降至5.37 kN,降幅31.6%,磨耗指数由6.65降至4.84,降幅为27.2%。
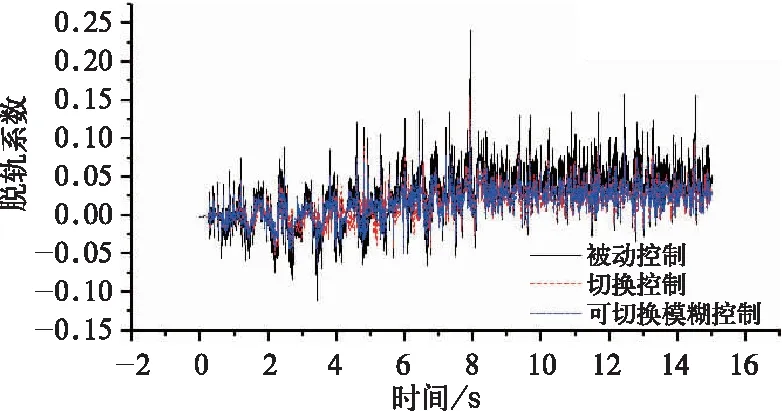
图9 半主动控制下车辆曲线通过的脱轨系数
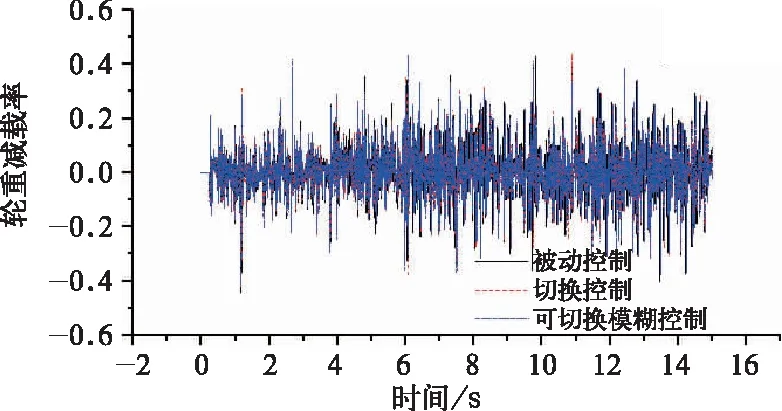
图10 半主动控制下车辆 曲线通过的轮重减载率
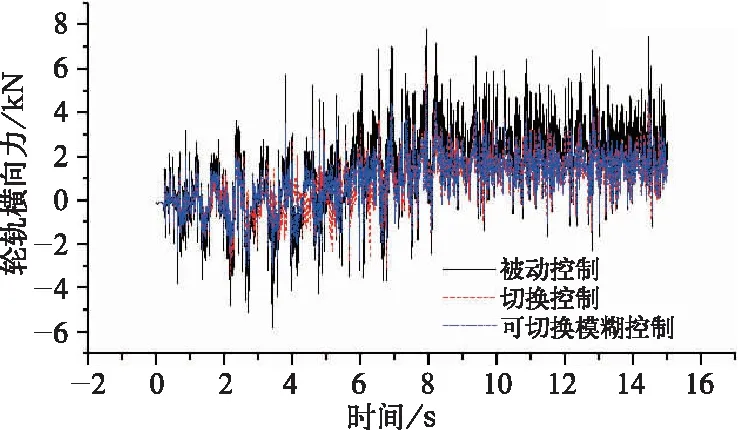
图11 半主动控制下车辆 曲线通过的轮轨横向力
4 结 论
通过建立高速车辆动力学模型仿真车辆运行工况,并与控制模型联合仿真,尝试解决高速车辆存在的横向稳定性与曲线通过性能相互矛盾的问题,得出结论如下:
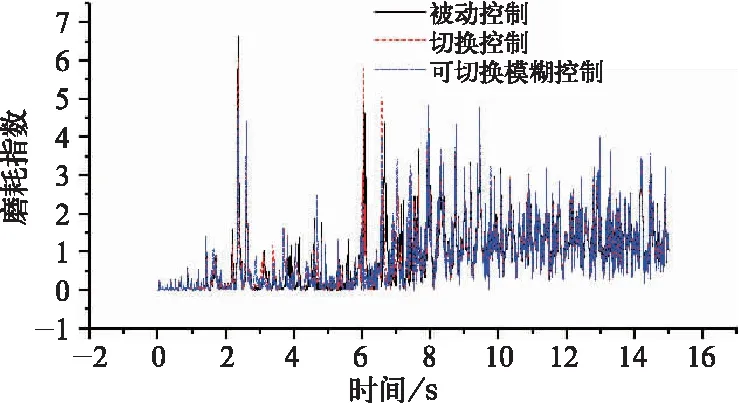
图12 半主动控制下车辆 曲线通过的磨耗指数
(1)提出了一种可切换半主动控制方法,以车体质心垂向位移为控制算法切换指标,自动调节抗蛇行减振器阻尼,使得车辆在直线轨道运行时,取得较高的阻尼力;通过曲线时,切换成较低的阻尼力。
(2)针对可切换控制方法中,车辆在直线和曲线轨道运行时,抗蛇行减振器只能在固定的阻尼特性之间切换,只有在特定运行条件下,动力学性能才能达到最优,且不能随路况及车辆实时运行状态调整其阻尼特性的问题,提出一种可切换模糊控制策略。
(3)车辆在直线运行工况下,与被动控制相比,可切换控制临界速度提高到890 km/h,可切换模糊控制临界速度提高到940 km/h;可切换模糊控制相对于被动控制抗蛇行减振器,车辆的横向稳定性和非线性临界速度得到了很大提高,且优于可切换控制模型。
(4)车辆在曲线轨道运行时,与被动控制相比,可切换控制与可切换模糊控制的抗蛇行减振器分别使车辆脱轨系数降低37.5%,50.0%,轮轨横向力降低22.7%,31.6%,磨耗指数降低8.6%,27.2%;可切换模糊控制模型的控制效果最优。
由仿真结果可得,可切换模糊控制要优于单一切换控制和被动控制,因此可切换模糊控制磁流变抗蛇行减振器可有效解决高速车辆提速过程中横向稳定性和曲线通过性能之间的矛盾。
