素环上的环同构及完全保交换性映射

张 婷，侯晋川

(太原理工大学 数学学院，太原 030024)

令R是环(或对合环，其对合运算记为*)，则对于每个正整数n，R上的n×n矩阵全体Mn(R)是一个环(或对合环)。令Φ:R→R是一个映射，对于任意n∈N,Φ可以自然地延拓为从Mn(R)到自身的一个映射Φn,其定义为

Φn((sij)n×n)=(Φ(sij))n×n.

注意到，如果Φ是R上的一个环同态(或*-环同构)，则对每一个n=1,2,…,Φn也是Mn(R)上的一个环同态(或*-环同构)。令(P)是环的某个性质，如果Φn保持性质(P),则称Φ是n-保持(P)的；如果对每个正整数n,Φ都是n-保持(P)的，则称Φ是完全保持(P)的。如果Φ是环同态且性质(P)是环同态的一个不变量，则Φ是完全保持(P)的。完全保持问题研究的是这一现象的逆问题，即，如果性质(P)是环同态的一个不变量，那么R上完全保(P)的映射是否是环同态，如何刻画这些完全保持映射。

算子代数和算子空间上的一些线性完全保持问题已经得到广泛的研究。例如，完全正线性映射和完全有界线性映射是算子代数和算子空间理论中非常重要的研究课题[1].HADWIN et al在文献[2]中讨论了B(H)上完全秩不增线性映射并对此类映射进行了刻画，之后文献[3]把[2]中的工作推广到B(X)上并在此基础上给出了初等算子的刻画；这里H为Hilbert空间，X为Banach空间，B(X)为X上有界线性算子全体构成的代数。文献[4-5]则分别给出有限von Neumann代数上完全保迹秩的线性映射和一般映射的刻画。文献[6-7]分别给出Banach空间上标准算子代数上的完全保可逆性满射和完全保谱满射的刻画。标准算子代数上完全保幂等性、平方幂零性、交换性和Jordan零积的一般满射的刻画可在文献[8-9]中找到。

本文继续对算子代数上的完全保交换性和斜交换性映射的刻画问题进行研究。本文在下述两个方面对已有的结论进行了推广或深化，一是在更多的算子代数上进行讨论，二是在标准算子代数的情形弱化了满射性假设。事实上，首先在更一般的纯代数框架下进行讨论，给出含单位元的素环(或素对合环)上完全保交换性(或斜交换性)满射的刻画。令R是含单位元I的素环，证明了满射Φ：R→R完全双边保交换性的充分必要条件是Φ具有形式Φ=LC∘π,其中C∈Z(R)是可逆元，π是R的环同构；令R是含单位元I的素对合环，其对合运算记为*,满射Φ：R→R完全双边保斜交换性的充分必要条件是Φ具有形式Φ=LC∘π,其中C∈Z(R)是可逆对称元，π是R的*-环同构。如果映射是保单位元的，即Φ(I)=I,则上述结果中环为素的假设可以去掉，即一般有单位环(对合环)上的满射是环同构(对合环同构)当且仅当它是保单位元的且完全双边保交换性(斜交换性)的。本文还将上述结论应用到C*-代数、von Neumann代数、Banach空间上标准算子代数、Krein空间上不定自伴标准算子代数及对称标准算子代数，获得这些算子代数上完全双边保交换性或斜交换性的满射的具体形式。对于标准算子代数的情形，映射的满射性假设可以减弱为值域包含所有的一秩幂等算子。

令R是一个环，R的中心为Z(R)={Z∈R∶AZ=ZA∀A∈R}.称R是素环如果对任意A,B∈R,ARB={0}蕴涵A=0或B=0;称环R是对合环或*-环如果存在一个可加映射*:R→R满足(AB)*=B*A*且(A*)*=A对所有A,B∈R成立。*称为对合环R的对合运算。记Q=Qml(R)是环R的极大左商环。Q的中心C=C(R)=Z(Q)称为环R的扩展中心，且有Z(R)⊆C.如果R是素的，则Q也是素的并且C是一个域。如果R是素对合环，则它的对称扩展中心CS={λ∈C∶λ=λ*}也是一个域(参见文献[10]).一个映射Φ:R→R称为环同态如果Φ是可加的且是可乘的。双射环同态称为环同构。类似地，当R是素对合环时，一个映射Φ:R→R称为*-环同态(或对合环同态)如果Φ是环同态且Φ(A*)=Φ(A)*对任意A∈R都成立。双射*-环同态称为*-环同构。对任意A∈R,将对角矩阵diag{A,A,…,A}∈Mn(R)记为A(n);记LA为R上的左乘子，即LAT=AT对任何T∈R成立。显然，LA是可加映射。对于映射Φ:R→R,我们称Φ是双边保交换性的如果对任意A,B∈R,AB=BA⟺Φ(A)Φ(B)=Φ(B)Φ(A);当R是对合环时，其对合运算记为*,称Φ是双边保斜交换性的如果对任意A,B∈R,AB=BA*⟺Φ(A)Φ(B)=Φ(B)Φ(A)*.

1 环同构和完全保交换性映射

在本节中，用映射的完全保交换性给出环同构的刻画。

定理1设R是含单位元I的素环且Φ:R→R是满射，则下列陈述等价：

1)Φ完全双边保交换性。

2)Φ2双边保交换性。

3) 存在可逆元C∈Z(R)和环同构π:R→R使得Φ=LC∘π.

证明:因为对每个正整数n,πn是Mn(R)上的环同构且Φn=(LC∘π)n=LC(n)πn，所以3)⟹1)⟹2)显然成立。下面只需证2)⟹3).假设Φ2双边保交换性。

断言1Φ(0)=0.

对于任意T∈R,有

将Φ2作用于上式可得

此蕴涵

Φ(0)2=Φ(0)Φ(T) .

(1)

根据Φ的满射性，存在T0∈R使得Φ(T0)=0.将T=T0代入等式(1)可得Φ(0)2=0.再取使得Φ(T1)=I的T1∈R,将其代入等式(1)可得Φ(0)=Φ(0)2=0.

断言2Φ是单射。

假设T,S∈R满足Φ(T)=Φ(S).因为

则有

将上式中的Φ(T)用Φ(S)来代替，有

由于Φ2是双边保交换性的，故有

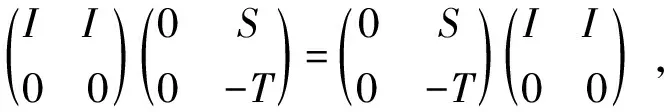
由此可得T=S.所以Φ是单射从而Φ是双射。

断言3Φ(I)∈Z(R).

对任意T∈R,因为

所以有

此蕴涵

Φ(I)Φ(T)=Φ(T)Φ(I)

(2)

对所有T∈R都成立。因Φ是满射，所以有0≠C=Φ(I)∈Z(R).根据R的素性可知R的扩展中心C=C(R)是一个域。故C在C中是可逆的。对任意的T∈R,令Ψ(T)=C-1Φ(T).由于Ψ2((Tij)2×2)=C-2(Φ(Tij))2×2且C-2∈C(R),易知，映射Ψ:R→C-1R仍然是2-双边保交换性的且Ψ(I)=I.

断言4Ψ是环同构。

对任意T,S∈R因为

有

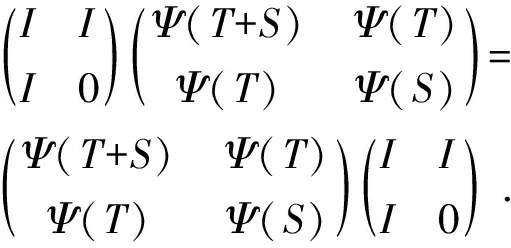
由此可知Ψ(T+S)=Ψ(T)+Ψ(S),即，Ψ是可加的。

对任意T,S∈R,因为Ψ是可加的并且

所以有

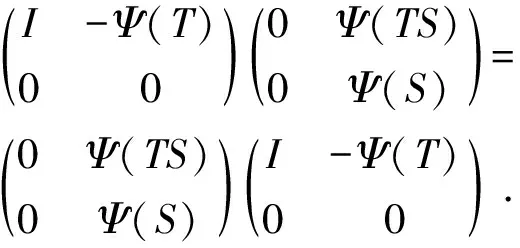
此蕴涵Ψ(TS)=Ψ(T)Ψ(S).所以Ψ是可乘的。因为R是一个环，Ψ的可乘性及可加性蕴涵C-1R也是一个环。因此，C-2=C-1I·C-1I∈C-1R,从而必有C-1∈R.所以，Ψ实际上是R的环自同构并且Φ=LC∘Ψ.令π=Ψ,则Φ=LC∘π.证毕。

由定理1的证明，如果假设Φ(I)是R中的可逆元，则环的素性假设可以去掉。即有

定理2设R是含单位元I的环且Φ:R→R是满射。如果Φ(I)是可逆的，则下列陈述等价：

1)Φ完全双边保交换性。

2)Φ2双边保交换性。

3)C=Φ(I)∈Z(R)且存在环同构π:R→R使得Φ=LC∘π.

下面的推论用完全保交换性的语言给出环同构的一种刻画。

推论1令R是含单位元I的环且Φ:R→R是保单位元的满射。则下列陈述等价：

1)Φ完全双边保交换性。

2)Φ2双边保交换性。

3)Φ是环同构。

现在将定理1应用到一些算子代数上。

令H是一个复Hilbert空间，如果M是B(H)的一个C*-子代数并且满足双换位子性质，即，M"=M,其中

M'={T:T∈B(H),TA=AT∀A∈M} ,

且M"=(M')',则称M是von Neumann代数。如果M的中心Z(M)=M∩M'=CI,则称M是因子。每个因子von Neumann代数都是素的。

推论2令M是一个因子von Neumann代数且Φ:M→M是一个满射。则下列陈述等价：

1)Φ完全双边保交换性。

2)Φ2双边保交换性。

3) 存在非零数c和M的环自同构π使得Φ=cπ.

对于矩阵代数和标准算子代数情形，可以弱化映射的满射性条件。下面的推论可以看作是文献[9]相应结论的推广。

推论3令X是实数或复数域F上的Banach空间且A是X上的标准算子代数。如果映射Φ：A→A的值域包含所有的一秩幂等算子，则下列陈述等价：

1)Φ完全双边保交换性。

2)Φ2双边保交换性。

3) 存在非零数c∈F，环自同构τ:F→F和τ-线性双射A:X→X使得Φ(T)=cATA-1对所有T∈A成立。进而，如果X是实的，则A是线性有界可逆算子；如果X是复的并且dimX=∞，则A是线性或共轭线性有界可逆算子。

证明：仅需证2)⟹3).假设2)成立。通过验证定理1的证明，易知对任意T∈A有Φ(0)2=Φ(0)Φ(T)(见式(1)).因为Φ的值域包含所有的一秩幂等算子，故对任意对任意一秩幂等算子x⊗f，有

Φ(0)2=Φ(0)x⊗f.

(3)

如果Φ(0)≠0，则存在x∈X使得Φ(0)x≠0.因为dimX≥2,故存在两个线性无关的泛函f1,f2∈X*使得x⊗f1和x⊗f2都是一秩幂等算子。根据式(3)有Φ(0)x⊗f1=Φ(0)2=Φ(0)x⊗f2,矛盾。因此我们有Φ(0)=0.类似于定理1的证明，可知Φ是单射，并且对任意算子T∈A都有Φ(I)Φ(T)=Φ(T)Φ(I)(见式(2)).特别地，Φ(I)与每个一秩幂等算子都是交换的，此蕴涵存在非零c∈F使得Φ(I)=cI.类似定理1的证明，Ψ=c-1Φ是A到自身的单射环同态。注意到一个非零算子A∈A是一秩的当且仅当对任意一秩幂等算子B,C,BAC=0蕴涵BA=0或AC=0.通过这个事实易证Ψ保算子的秩一性。Ψ的可乘性蕴涵Ψ(FI)⊆FI,由此可以推出对任意一秩幂等算子x⊗f都有

Ψ(Fx⊗f)⊆FΨ(x⊗f).

所以所有一秩算子都包含在Ψ的值域中且Ψ|FI+F(X)是FI+F(X)上的环同构，其中F(X)表示B(X)中有限秩算子全体构成的子代数。因此，由众所周知的结果，存在环自同构τ:F→F和τ-线性双射A:X→X使得Ψ(F)=AFA-1对所有F∈FI+F(X)成立。现在，对任何T∈A,因为

Ψ(T)A(x⊗f)A-1=Ψ(Tx⊗f)=AT(x⊗f)A-1=ATA-1A(x⊗f)A-1

对所有一秩算子x⊗f都成立，故有Ψ(T)=ATA-1.这就证明了，Φ(T)=cATA-1对任何T∈A都成立。通过文献[11]和[12(定理2.4.2)]可知关于A的断言也是正确的。证毕。

特别地，有

推论4令Mn(F)是实数或复数域F上的n×n矩阵全体构成的代数且Φ:Mn(F)→Mn(F)是一个映射，如果Φ的值域包含所有的一秩幂等矩阵，则下列陈述等价：

1)Φ完全双边保交换性。

2)Φ2双边保交换性。

3) 存在非零数c,环自同构τ:F→F和可逆矩阵A∈Mn(F)使得Φ(T)=cATτA-1对所有T∈Mn(F)成立。这里对任意T=(tij)∈Mn(F),Tτ=(τ(tij)).

2 *-环同构和完全保斜交换性映射

在本节中，讨论素*-环上的*-环同构和完全保斜交换映射的关系。

下面是本节的主要定理。

定理3令R是含单位元I的素对合环，其对合运算记为*.令Φ:R→R是一个满射。则下列陈述等价：

1)Φ完全双边保斜交换性。

2)Φ2双边保斜交换性。

3) 存在可逆对称元C∈Z(R)和R的*-环同构π使得Φ=LC∘π.

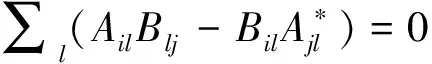
Φn(A)Φn(B)-Φn(B)Φn(A)*=
(Cπ(Aij))(Cπ(Bij))-(Cπ(Bij))(Cπ(Aij))*=
(C2π(∑lAilBlj))-(C2π(∑lBilAjl*))=
(C2π(∑l(AilBlj-BilAjl*)))=0 .

反之，Φn(A)Φn(B)-Φn(B)Φn(A)*=0蕴涵C2π(∑l(AilBlj-BilAjl*))=0对任意i,j∈{1,2,…,n}都成立。因为R是素的，且C≠0,故C在扩展中心C(R)中可逆，由此可知对任意T∈R,C2T=0蕴涵T=0.根据π(∑l(AilBlj-BilAjl*))=0和π的单射性可得∑l(AilBlj-BilAjl*)=0.故必有AB=BA*=0.因此，对任意正整数n,Φn是双边保斜交换性映射。

所以3)⟹1)⟹2)成立。下面仅需证明2)⟹3)成立。假设Φ2双边保斜交换性。

断言5Φ(0)=0.

对任意T∈R,有

将Φ2作用于上式可得

此蕴涵

Φ(0)2=Φ(T)Φ(0) .

(4)

类似定理1中断言1的证明，可知Φ(0)=0.

断言6Φ是单射。

假设T,S∈R满足Φ(T)=Φ(S).因为

有

将上式中的Φ(T)用Φ(S)来代替，有

由于Φ2双边保斜交换性，故可得

此蕴涵T=S.因此Φ是单射从而Φ是双射。

断言7Φ(I)=Φ(I)*且Φ(I)∈Z(R).

对任意T∈R,因为

所以有

由此可得，对所有T∈R有

Φ(I)Φ(T)=Φ(T)Φ(I)*.

(5)

由于Φ是满射，存在T0∈R使得Φ(T0)=I.将T=T0代入等式(5)有Φ(I)=Φ(I)*.因此，Φ(I)是对称元且对任意T∈R有Φ(I)Φ(T)=Φ(T)Φ(I).根据Φ的满射性，有C=Φ(I)∈Z(R).

根据断言6，可知C≠0.R的素性蕴涵C在C(R)中可逆。对任意的T∈R,令Ψ(T)=C-1Φ(T).根据断言7，易知Ψ:R→C-1(R)是2-双边保斜交换性的且Ψ(I)=I.

断言8 对任意T∈R,Ψ(T*)=Ψ(T)*.

对任意T∈R,因为

所以有

因而，Ψ(T*)=Ψ(T)*.

断言9Ψ是可加的。

对任意T,S∈R,因为

所以有

因此Ψ(T+S)=Ψ(T)+Ψ(S),即，Ψ是可加的。

断言10Ψ是*-环同构且C-1∈R.

对任意T,S∈R,因为

所以有

此蕴涵Ψ(TS)=Ψ(T)Ψ(S).因而Ψ是*-环同构。由此可知，C-1R是*-环。特别地，C-2∈C-1R表明C-1∈R,即C在R中可逆。因此Ψ实际上是R的*-环同构并且Φ=LC∘Ψ.令π=Ψ,则有Φ=LC∘π.证毕。

由定理3的证明，如果假设Φ(I)是R中的可逆元，则对合环的素性假设可以去掉。即有

定理4设R是含单位元I的对合环，其对合运算记为*.令Φ:R→R是满射，如果Φ(I)是可逆的，则下列陈述等价：

1)Φ完全双边保斜交换性。

2)Φ2双边保斜交换性。

3)C=Φ(I)∈Z(R),C=C*且存在*-环同构π:R→R使得Φ=LC∘π.

下面的推论用完全保斜交换性的语言给出*-环同构的一种刻画。

推论5令R是含单位元I的对合环，其对合运算记为*.令Φ:R→R是一个保单位元的满射。则下列陈述等价：

1)Φ完全双边保斜交换性。

2)Φ2双边保斜交换性。

3)Φ是*-环同构。

下面将定理3应用到一些算子代数上。

推论6令A是含单位元I的素C*-代数且Φ:A→A是一个的满射。则下列陈述等价：

1)Φ完全双边保斜交换性。

2)Φ2双边保斜交换性。

3) 存在实数c≠0和A的*-环同构π使得Φ=cπ.

证明：根据文献[13](推论2.3)可知，素C*-代数的扩展中心是复数域C.因此，CS(A)=R.故由定理3可知推论是显然的。证毕。

每一个因子von Neumann代数都是含单位元的素C*-代数。因此根据推论6，下面的推论是直接的。

推论7令M是因子von Neumann代数且Φ:M→M是一个满射。则下列陈述等价：

1)Φ完全双边保斜交换性。

2)Φ2双边保斜交换性。

3) 存在实数c≠0和M的*-环同构π使得Φ=cπ.

显然，每个不定自伴标准算子代数A是一个含单位元I和具有对合运算†的素对合环。根据定理3，如果Φ是满射，则以下推论是正确的。然而在此情形，可以弱化映射的满射性条件。

推论8令H是实或复的Krein空间且dimH≥2.令A⊆B(H)是不定自伴标准算子代数，如果映射Φ:A→A的值域包含所有一秩幂等算子，则下列陈述等价：

1) 对任意正整数n，Φn:Mn(A)→Mn(A)满足，对任意的A,B∈Mn(A),

AB=BA†⟺Φn(A)Φn(B)=Φn(B)Φn(A)†.

2)Φ2:M2(A)→M2(A)满足，对任意A,B∈M2(A),

AB=BA†⟺Φ2(A)Φ2(B)=Φ2(B)Φ2(A)†.

3) 存在实数c≠0和†-酉或共轭†-酉算子U:H→H使得Φ(T)=cUTU†对任意T∈A成立。

证明：一个有界线性或者共轭线性算子U:H→H称为†-酉算子如果U†U=UU†=I.所以3)⟹1)⟹2)是显然的。为证2)⟹3)，假设条件2)成立，应用定理3，易知对任意T∈A有Φ(0)2=Φ(T)Φ(0)(见式(4)).因为Φ的值域包含所有一秩幂等算子，所以对任意一秩幂等算子x⊗f都有

Φ(0)2=(x⊗f)Φ(0) .

(6)

此蕴涵Φ(0)2是一秩算子。如果Φ(0)≠0，则一定存在某个f∈H使得Φ(0)†f≠0.由于dimH≥2，可找到两个线性无关的向量x1,x2∈H使得〈x1,f〉=〈x2,f〉=1.根据等式(6),有Φ(0)2=xi⊗Φ(0)†f,此时一秩算子Φ(0)2的值域包含{x1,x2}，矛盾。因此，Φ(0)=0.

下面证明存在非零实数c使得Φ(I)=cI.类似定理3的证明，可知Φ是单射且Φ(I)Φ(T)=Φ(T)Φ(I)†对所有T∈A都成立。特别地，对所有一秩幂等算子x⊗f都有

Φ(I)x⊗f=(x⊗f)Φ(I)†=x⊗Φ(I)f.

(7)

类似定理3证明，可知对任意T∈A有Φ(T†)=Φ(T)†,且存在†-环同态π使得Φ=cπ.因为π是值域包含所有的一秩幂等算子的环同态，且根据推论3的证明，存在F上的环自同构τ和τ-线性双射A:H→H使得π(T)=ATA-1对所有T∈A成立。此外，根据π(T†)=π(T)†对任意T∈A成立，有

AT†A-1=(ATA-1)†=(A-1)†T†A†

对任意T∈A都成立。由此可得A-1=A†,即AA†=A†A=I.对任意实数λ和任意†-自伴算子T∈A，λT仍是†-自伴算子，因此A(λT)A†=τ(λ)ATA†是†-自伴的。因此τ(λ)必为实数，即，τ把实数映为实数。所以τ必定是恒等映射或共轭映射，即A是线性或共轭线性的。令U=A，则3)成立，证毕。

令H是复Hilbert空间且{ei}i∈Λ是H的一组

推论9令H是复Hilbert空间且dimH≥2.令A⊆B(H)是给定一组基下的对称标准算子代数，如果映射Φ:A→A的值域包含所有一秩幂等算子。则下列陈述等价：

1) 对任意正整数n，Φn:Mn(A)→Mn(A)满足条件：对任意的A,B∈Mn(A),

AB=BAT⟺Φn(A)Φn(B)=Φn(B)Φn(A)T.

2)Φ2:M2(A)→M2(A)满足条件：对任意A,B∈M2(A),

AB=BAT⟺Φ2(A)Φ2(B)=Φ2(B)Φ2(A)T.

3) 存在复数α≠0,C上的自同构τ和τ-线性双射A:H→H使得Φ(T)=αATA-1对所有T∈A都成立。对于dimH=∞的情形，A是线性或共轭线性的有界可逆算子。

证明：3)⟹1)⟹2)显然。类似推论8的证明，可得对所有T∈A都有Φ(TT)=Φ(T)T.且存在非零复数α,C上的自同构τ和τ-线性双射A:H→H使得Φ(T)=αATA-1对所有的T∈A都成立。对于dimH=∞的情形，A是有界可逆线性或共轭线性的。根据Φ(TT)=Φ(T)T,易知A-1=AT.所以3)成立，证毕。