热冲击作用下花岗岩温度场分布规律数值模拟研究

2018-11-15熊贵明郤保平吴阳春陈路海

太原理工大学学报 2018年6期

熊贵明，郤保平,b，吴阳春，陈路海

(太原理工大学 a.矿业工程学院，b.原位改性采矿教育部重点实验室，太原 030024)

近年来，为扎实推进经济持续健康发展，我国大力发展高效清洁能源产业，坚持走绿色低碳循环发展的新路子。干热岩是一种清洁安全高效的能源资源，对干热岩的开发利用有利于增加清洁能源供给，优化能源结构，提高能源综合利用效率，建立多元供应体系，对保障国家能源安全有着重要意义。我国干热岩资源储量巨大，初步估算3～10 km深处干热岩资源总计为2.5×1025J，相当于8.56×1014t标煤[1]。特别是干热岩发电技术可大幅度降低温室效应和酸雨对环境的影响，且不受季节、气候制约，可以有效取代煤炭、石化能源消耗，有效保护生态环境。更为重要的是干热岩开发成本低，利用干热岩发电的成本仅为风力发电的1/2，或太阳能发电的1/10.正因为干热岩具有这么多优点，干热岩的开发备受关注。

自20世纪70年代初学者们提出干热岩开发构想以来，很多国家都投入了大量人力财力进行研究[2-4]。到目前为止，国内外对干热岩的生热、导热、控热、储热、释热构造和规律性研究仍然很少[5]。我国对干热岩开发研究较晚，且研究主要集中在勘探、钻井、压裂和监测等方面，目前主要存在以下问题[6-9]：

1) 在干热岩钻井过程中，如何控制钻井液导致的井壁围岩坍塌崩落、缩颈或地层破裂等失稳问题。

2) 在热储层建造过程中，怎样通过水力致裂、热激发或化学激发产生杂乱无章、分布均匀、没有主流方向的裂缝网络等裂缝扩展问题。

3) 在工质与岩石进行热交换提取热量的过程中，如何选择工质(水、液氮等)、流速、注液压力和开采年限等参数，确保经济利益最大化。

由此可以看出，在干热岩开发的整个过程中，热冲击作用会引起岩体内的温度场重新分布，进而产生热应力，促使岩石热力学性质发生变化[10-14]。因此研究干热岩在热冲击作用下的温度场分布规律是干热岩开发的基础。

研究干热岩开发整个过程，必须围绕岩石在热冲击作用下的温度场分布规律这一主线进行。本文采用Comsol Multiphysics 5.3a软件，依据某干热岩项目人工热储层的花岗岩参数，建立热冲击作用下花岗岩的温度场数学物理模型；通过对其进行数值模拟，分析热冲击作用下花岗岩在不同工质(H2O、液态CO2和液N2)和初始温度时的温度场变化规律。

1 花岗岩温度场数学模型

热冲击和热破裂两个概念的内涵如下：

1) 岩石受到急剧的加热和冷却时，其内部产生很大的温差，从而引起很大的冲击热应力，这种现象称为热冲击。一次大的热冲击所产生的热应力能超过岩石的屈服极限，从而导致岩石失稳。

2) 岩石受热后，由于其内部各种造岩矿物颗粒的热膨胀系数不同，岩石内部产生热应力并产生裂缝；在热应力作用下岩石的内部裂缝逐渐扩展，裂缝相互连通形成裂缝网络，从而引起储层岩石物理性质(孔隙度、渗透率等)的改变。这种由热应力引起的岩石破裂称为岩石热破裂。

总之，热冲击强调过程，而热破裂强调结果。本文采用热冲击速度、温度梯度等概念分别去阐释岩石表面和内部的温度场分布规律。其中，热冲击速度是指单位时间内温度变化量，温度梯度是指单位长度内温度变化量。

1.1 基本假设

干热岩的主要成分是花岗岩，花岗岩由多种成矿物质组成。热冲击作用时，岩石内部多种物质因具有不同的热效应，相互制约、相互影响，因此热冲击过程是一个相当复杂的过程。本文假设花岗岩仅受温度场的影响。此外，还对模型作如下假设：

1) 花岗岩各向同性，不发生相变。

2) 花岗岩的初始温度是均匀的。

3) 花岗岩热冲击过程中忽略热对流和热辐射，只考虑热传导。

4) 花岗岩在热冲击作用下的温度变化过程满足局部热平衡。

1.2 岩石瞬态热传导模型

根据传热学理论，由能量守恒定律，得三维圆柱体瞬态温度场方程[15]：

(1)

岩石内部没有热源，即热流量Φ=0，且圆柱体的几何形状和温度作用都对称于圆柱体的中心轴线。因此这一问题属于空间轴对称问题，式(1)可简化为：

(2)

式中：ρ为岩石密度；c为岩石比热容；k为岩石导热系数；T为岩石瞬时温度；τ为时间；r为岩石试件半径；z为岩石试件高度。为了简化模型，将岩石的热力学参数(弹性模量、热膨胀系数和泊松比)取为常数。

为了得到花岗岩温度值的唯一结果，须给出一定的边界条件，具体如下。

第一类边界条件：取温度为定值，即

T1=C.

(3)

第二类边界条件：给定边界上为绝热边界，即

(4)

第三类边界条件：给定边界上物体表面与周围流体间的表面传热系数h及流体的温度Tf，但不发生对流传热，即

(5)

综合式(2)—(5)可得出，热冲击作用下花岗岩温度场的物理模型如下:

(6)

式中：T为岩石边界温度；C为常数；n为岩石换热表面的外法线的长度；h为岩石表面传热系数；Tw为岩石表面温度；Tf为流体温度；r0为岩石的最大半径；b为岩石最大高度；T0为岩石初始温度。

2 热冲击作用下花岗岩有限元模型的建立

2.1 模型建立

图1 花岗岩试件数值计算物理模型(单位：mm)Fig.1 The granite physical model of numerical calculation

选取某干热岩项目人工热储层花岗岩为研究对象，对室内实验进行数值模拟。模拟对象采用φ50 mm×100 mm的圆柱体花岗岩试件，见图1。由于该模型所加载的边界条件均满足轴对称条件，在三维模型中取一截面进行研究。在这里规定，沿圆柱体底面圆的半径方向为径向，沿圆柱体的高度方向为轴向。为了便于研究花岗岩的温度场分布规律，在花岗岩试件上布置监测点1—10(见图1)。监测点1—6相邻两点之间距离为5 mm，监测点6—9相邻两点之间距离为25 mm.

2.2 参数选取

模拟中选取的花岗岩的比热容c=850 J/(kg·K)，密度ρ=2 600 kg/m3，导热系数λ=2.9 W/(m·K)，泊松比μ=0.25，弹性模量E=60 GPa，热膨胀系数α=7×10-6K-1.

2.3 花岗岩热冲击模拟实验方案

花岗岩试件的初始温度分别为373.15，473.15，573.15，673.15，773.15，873.15 K；工质分别为常温水(293.15 K)、液态二氧化碳(236.15 K)和液氮(77.15 K).本模拟方案为：将花岗岩试件加热到初始温度后，将沿轴向1/4部分的花岗岩试件浸入不同工质；按照表1方案模拟花岗岩试件热冲击下温度的变化情况。其中，底部和其他部分均为绝热边界。以图1截面图中左下角O为原点，则监测点1—10的坐标分别为(0,25)，(5,25)，(10,25)，(15,25)，(20,25)，(25,25)，(25,50)，(25,75)，(25,100)，(0,100).

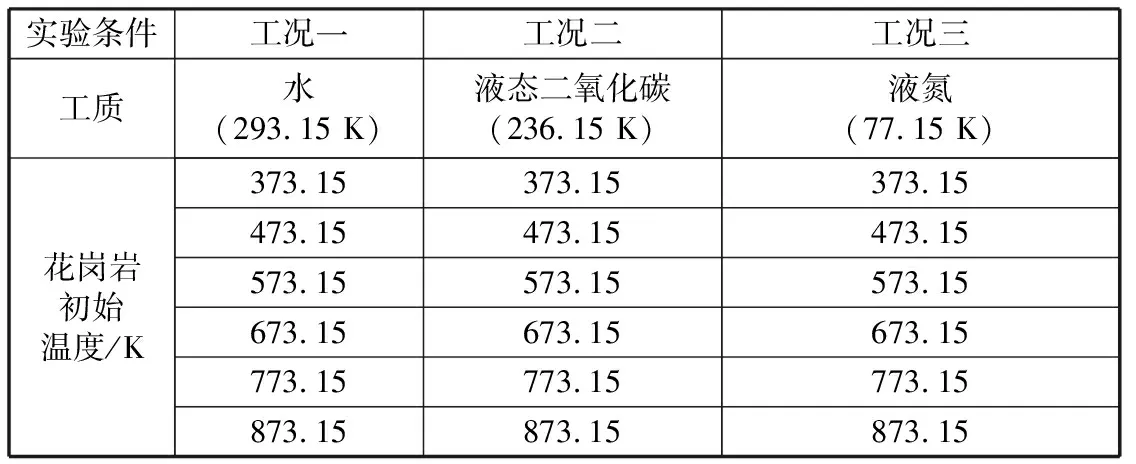
表1 数值模拟实验方案Table 1 Numerical simulation experiment scheme

2.4 网格划分与求解设置

网格划分是数值计算的重要一环，网格划分的质量直接影响整个模型计算过程的精细程度。本模型为二维轴对称，对称轴为r=0，采用Comsol Multiphysics 5.3a软件网格绘制功能中的三角形网格进行划分。

在Comsol Multiphysics 5.3a软件中添加瞬态研究，热冲击时间设置为500 min，时间间隔设为0.1 min，使用参数化扫描，求解花岗岩在热冲击作用下的温度场分布规律。

3 结果与讨论

3.1 热冲击作用下花岗岩温度场总体变化规律

在干热岩开发中，从钻井、人工热储建造到热能提取整个过程均涉及到岩石的温度场，因此，研究花岗岩温度场的变化规律是干热岩开发最关注的信息点。

由图2可知，伴随着热冲击作用，无论是哪种工质，热冲击作用下花岗岩的温度场均以波的形式呈倒梯形向内部以一定的速度传播；工质接触的面积越大，温度场传播速度越快；热冲击波传播所经过的点温度会突然降低，直至最后趋于稳定。

图2(a)、(b)和(c)中的温度场云图仅能看到温度场特定时间的分布云图，不能明显地看出温度随时间的变化规律。

花岗岩初始温度：873.15 K图2 不同工质下花岗岩热冲击作用1 min时剖面温度场云图Fig.2 Temperature field cloud map of 1min time profile of hot shock of granite under different working conditions

在不同工质与初始温度的条件下，热冲击作用时花岗岩的温度随时间的增加而降低。取离冲击波源最远的监测点10为研究对象，如图3所示。在所研究的温度范围内，对于工质一(H2O)而言，当初始温度小于473.15 K时，花岗岩在1.1 min波及到整块岩石；当初始温度大于473.15 K时，花岗岩在1.4 min波及到整块岩石。此外，初始温度小于673.15 K时，花岗岩达到与工质相同温度的时间随着初始温度的升高而增加；而初始温度大于673.15 K时，花岗岩随初始温度的升高所需时间减少；当初始温度大于773.15 K时，花岗岩不再发生变化，且保持在236 min.

对于工质二(液态CO2)而言，当初始温度小于473.15 K时，花岗岩在1.2 min波及到整块岩石；当初始温度大于473.15 K时，花岗岩在1.5 min波及到整块岩石；同时，达到与介质相同的温度的变化规律同工质一；但在初始温度大于773.15 K时，花岗岩不再发生变化且保持在243 min.

图3 热冲击作用下花岗岩温度随时间的变化Fig.3 Temperature change with time under hot shock

对于工质三(液N2)而言，花岗岩在1.5 min波及到整块岩石，与岩石的初始温度无关；同时，达到与介质相同的温度变化规律同工质一；但在初始温度大于773.15 K时，花岗岩不再发生变化且保持在294 min.

由此可见，在不同的工质中，花岗岩温度场的热冲击作用在100 s左右波及到整块花岗岩且变化规律一致，可见热冲击具有时间效应；随着工质温度的降低，达到与介质相同的温度的时间变长；在初始温度673.15～773.15 K之间存在一个温度阈值，可能会引起花岗岩的相态转变，进而影响花岗岩温度场的变化规律。

由于热冲击作用下花岗岩的温度场分布规律一致，下面仅选取工况一对热冲击作用下花岗岩表面及内部温度场进行讨论与分析。

3.2 热冲击作用下花岗岩表面温度场变化规律

花岗岩表面监测点的热冲击速度随时间变化的曲线如图4.可见，热冲击作用下花岗岩的热冲击速度随时间的增加而降低；花岗岩表面在同一时间任一点的热冲击速度相等，表明热冲击作用下的花岗岩温度是以冲击波的形式向前传递，进而影响花岗岩的温度场分布。

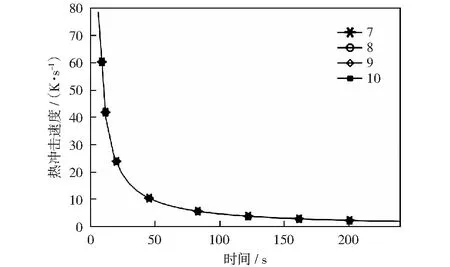
花岗岩初始温度：473.15 K图4 花岗岩表面热冲击速度随时间的变化Fig.4 Hot shock velocity of granite surface changes with time

花岗岩表面某点在不同初始温度下的热冲击速度随时间变化曲线如图5所示。由图5可知，热冲击作用下花岗岩温度在15 s之内迅速下降；随着时间的增加，热冲击速度迅速降低且趋于零。可见热冲击作用具有瞬时性，且热冲击速度随着花岗岩初始温度的升高而增大。

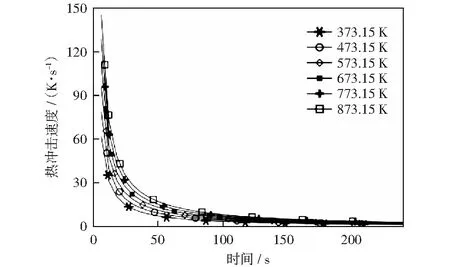
图5 花岗岩表面点7热冲击速度随时间的变化Fig.5 Hot shock velocity of granite surface point 7 with time

3.3 热冲击作用下花岗岩内部温度场变化规律

取花岗岩内部监测点1—5，各监测点温度梯度随时间变化的曲线见图6.可以看出，热冲击作用下花岗岩沿径向的温度梯度随时间增加呈现先增加后减小，最后趋于零；花岗岩内部监测点5、4、3、2、1达到温度梯度峰值所用的时间分别是0，0.8，1.2，3.3，3.6 min.在热冲击作用边界上，花岗岩瞬间温度梯度达到相当大的值；离热冲击作用边界距离越远，沿径向热传导温度梯度峰值越低且所用的时间越长，说明热冲击作用波沿径向的传播过程会沿程损失，热冲击作用程度随热边界距离增大而减弱。

初始温度：473.15 K图6 花岗岩沿径向温度梯度随时间的变化Fig.6 Temperature gradient of the granite in the radial direction changes with time

由于各监测点温度场变化规律一致，选取点1研究在不同初始温度下花岗岩内部温度场的变化，见图7.图7显示：热冲击作用下的花岗岩随着初始温度的升高，温度梯度增大；不同初始温度的花岗岩热冲击温度梯度随时间的增加呈现先增加后减小，最后趋于零。经监测，当花岗岩的初始温度为373.15 K时，其温度梯度峰值是1 395 K/m；当花岗岩初始温度分别为473.15，573.15，673.15，773.15，873.15 K时，其温度梯度峰值分别是373.15 K时温度梯度峰值的2.30，1.61，1.35，1.26，1.20倍。这说明温度差越大，热冲击作用越强烈，岩石中热量损失自然越大。

图7 不同初始温度下花岗岩点1温度梯度随时间的变化Fig.7 Variation of temperature gradient of granite point 1 with time at different temperatures

综上所述，花岗岩的热冲击温度变化曲线可分为三个阶段：第一阶段为温度加速变化阶段，温度快速增加，温度梯度随时间的增加呈直线增大到峰值；第二阶段为温度减速变化阶段，温度减速增加，温度梯度随时间的增加由峰值减小到零；第三阶段为温度稳定阶段，温度不再变化，温度梯度为零，达到热平衡。

3.4 热冲击作用下花岗岩表面温度实验与数值模拟结果对比

由于目前实验设备的限制，热冲击作用下花岗岩的物理实验只能观测花岗岩表面的温度场规律。因此，选取工质一(H2O)，将数值模拟所得花岗岩表面在热冲击作用下5 s时热冲击速度随温度的变化曲线与花岗岩试件在相同条件下实验所得的曲线进行对比，结果如图8所示。从热冲击速度随温度的变化趋势来看，数值模拟与物理实验得到的结果相差不大。但数值模拟建立在简化的基础上，未能真实地反映花岗岩本身性质。

图8 花岗岩表面热冲击速度随初始温度变化的实验与模拟结果对比Fig.8 Comparison of experimental and simulation results of thermal shock velocity of granite surface with initial temperature