基于双向RRT算法的管线路径规划及建模仿真

王素琴，王 飞，袁建平，陈晓龙，陈显龙

(1.华北电力大学 控制与计算机工程学院，北京 102206；2.北京恒华伟业科技股份有限公司，北京 100011)

管线的种类和数量日益增多，大到保障城市正常运行的各类工程管线，小到设备内部连接各种元器件的线缆。管线敷设环境越来越复杂，如何更加快速、合理地进行管线的路径规划至关重要。

管线路径规划问题是指在给定的空间内，从指定起点到终点，设计一条不与其他物体发生干涉，同时又满足各种约束条件的路径。路径规划问题的求解方法很多，如遗传算法[1-2]、蚁群算法[3]、A*算法[4-6]、RRT算法[7]。PARK et al[8]针对航空航天电缆设计和生产提出了基于Agent的二维电缆路线设计。ITO[9]采用遗传算法来进行管线布局设计中路径的交互式规划。权建洲等[10]提出基于改进A*算法的电子制造装备布线路径搜索方法，引入评估函数优化搜索。吴保胜等[11]提出了基于重力规则的蚁群算法路径搜索策略。上述算法一般需要对搜索空间进行栅格化建模；当搜索空间较大时，会占用大量存储空间，影响计算效率。另外这些算法往往容易陷入局部最优解。

快速扩展随机树算法(RRT)是一种树形数据存储结构和算法，通过不断递增的方法建立，用于快速遍历空间的未探索区域。RRT算法在进行路径规划时不需要对环境进行具体建模，灵活性高，对场景有很好的适应性。刘潇等[12]提出了基于障碍物与目标吸引的改进快速扩展随机树算法用于线缆自动布线。徐联杰等[13]提出了基于障碍物碰撞信息的快速搜索随机树改进算法。RRT算法虽然能够在较短的时间内搜索出一条或多条路径，但是无法进行修改，所求路径为折线段，无法满足部分曲线路径弯曲半径的要求，交互性较差，不满足工程的实际需要。

考虑到弯曲变形、规划环境对管线路径规划的影响，本文使用双向RRT算法规划出一条路径后，引入Catmull-Rom样条曲线对路径关键点进行曲线拟合，添加了管线路径弯曲半径的约束，同时在虚拟环境中实现三维管线路径规划的模拟仿真及调整。此算法进一步提高了RRT算法在管线路径规划中的适应性和稳定性。

1 管线路径规划问题分析

管线按可弯曲程度分为可弯曲管线和不易弯曲管线。通过某些加工措施易将其弯曲的管线为可弯曲管线，如电信电缆、电力电缆等；通过加工措施不易将其弯曲的管线或强行弯曲损坏的管线为不易弯曲管线，如给水管道、电信管道等。管线路径规划问题也可以看作碰撞球的干涉问题[11]，即在三维环境中，以路径离散点为球心，球直径略大于管线直径(管线需要与障碍物保留一定的间隙，因此碰撞球的直径需要大于管线直径，大小可按照工艺要求设定，一般设为管线半径的1.2倍)，进行碰撞干涉检测。如果该碰撞球沿着路径进行搜索时不与环境中的障碍物发生干涉，那么这条路径是可行的。

对部分可弯曲管线进行路径规划设计时，还需要考虑最小弯曲半径的约束。由于这类管线绝缘及其构造特性要求，任何敷设方式及其全部路径均应满足最小弯曲半径要求。以电力电缆为例，单芯电缆的最小弯曲半径不小于电缆外径的15倍，多芯电缆的最小弯曲半径不小于电缆外径的10倍。

2 管线路径规划方法

2.1 基本RRT算法

RRT算法是一种常见的用于机器人路径规划的方法，它本质上是一种随机生成的数据结构——树，该算法自LAVALLE[14]提出以来已经得到了极大的发展，到现在依然有改进的RRT不断地被提出。

在RRT算法进行路径规划前，需要设置一些参数，包括路径搜索的起点qinit，终点qgoal，搜索步长l，最大搜索次数N等。然后创建扩展随机树T，以qinit为随机树的根节点。然后根据图1所示的节点扩展方法进行循环扩展，其中l表示搜索步长，具体步骤如下。

1) 采用随机采样的方法得到一个随机采样点qrand.

2) 找到距离采样点qrand最近的树节点qnear，进行节点扩展得到待定节点qnew.

3) 如果从qnear到qnew发生碰撞干涉，舍弃qnew进入下一次循环。

4) 如果qnear到qnew不发生碰撞干涉，将qnew加入扩展树，作为qnear的子节点。判断qnew是否足够接近qgoal，若足够接近，则直接与终点相连，循环终止，否则进入下一循环。

图1 节点扩展Fig.1 Node expansion

2.2 节点扩展策略优化

基本RRT算法在节点扩展时，由于qrand点的生成是随机的，导致了随机树扩展过于分散，且搜索时间过长，甚至在设定的有限次循环中无法到达目标点。针对这一问题，可以在节点扩展时，根据随机概率决定qrand是目标点还是随机点，增加qrand为qgoal的概率，当qrand为目标点时，节点扩展方向为目标方向，加快随机树到达目标点的速度。引入路径缓存[15]的方法，在随机树搜索路径时以一定概率选择之前成功规划路径上的节点，使随机树的搜索更高效。

2.3 双向扩展随机树

双向快速扩展随机树(BI-RRT)是在扩展策略上对基本RRT算法进行改进[16]，从起点和终点各自创建一棵扩展随机树。在每次循环过程中，先扩展其中一棵随机树，然后尝试将另一棵随机树扩展到当前新扩展的节点，使两棵扩展随机树朝向对方扩展；两棵随机树交替扩展，直至两棵随机树节点相遇(距离小于预设值)。基本RRT和双向RRT算法在二维路径规划上的效果对比如图2所示。

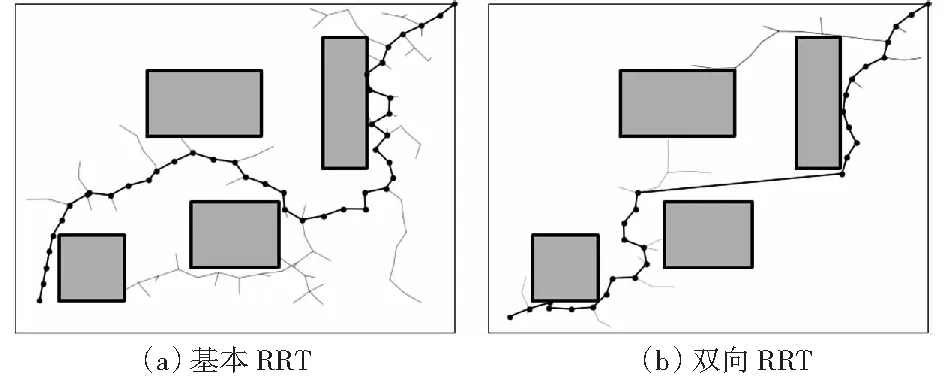
图2 RRT和BI-RRT比较Fig.2 Comparison of RRT and BI-RRT

虽然双向RRT算法在增加新节点时要判断是否可以将两棵树连接起来，增加了资源的消耗，但是提高了随机树扩展的效率和精度。

2.4 路径平滑处理

经过BI-RRT算法规划出来的原始路径含有许多冗余节点，不能直接作为管线路径，需要采用贪心算法来过滤这些冗余节点，从而获得更优化的路径规划结果。如图3所示，从起点qinit开始，依次寻找能够无碰撞连接终点qgoal的顶点，记录此点q'(1)，再从起点qinit开始，依次寻找能够无碰撞连接q'的顶点，记录此点q'(2)，直到起点qinit和q'(x)能够无碰撞连接，将所有的q'(x)连接就得到了平滑后的路径。

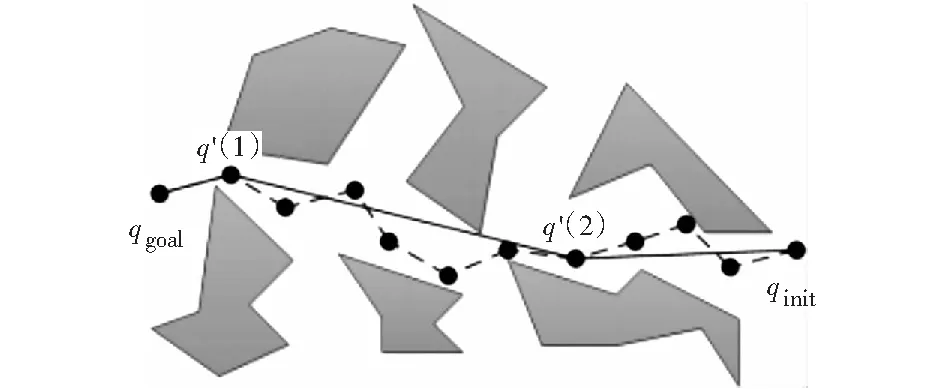
图3 路径平滑处理Fig.3 Path smoothing

2.5 基于关键点的曲线拟合

经过平滑处理的路径是由离散点形成的折线段组成，通常不满足可弯曲管线敷设要求，因此还需要进行折线段的光滑拟合。本文采用Catmull-Rom曲线对路径离散点进行拟合。Catmull-Rom曲线是由4个控制点P0，P1，P2，P3定义的插值样条曲线，绘制从P1到P2的曲线，如图4所示。

Catmull-Rom曲线的构造公式见式(1).

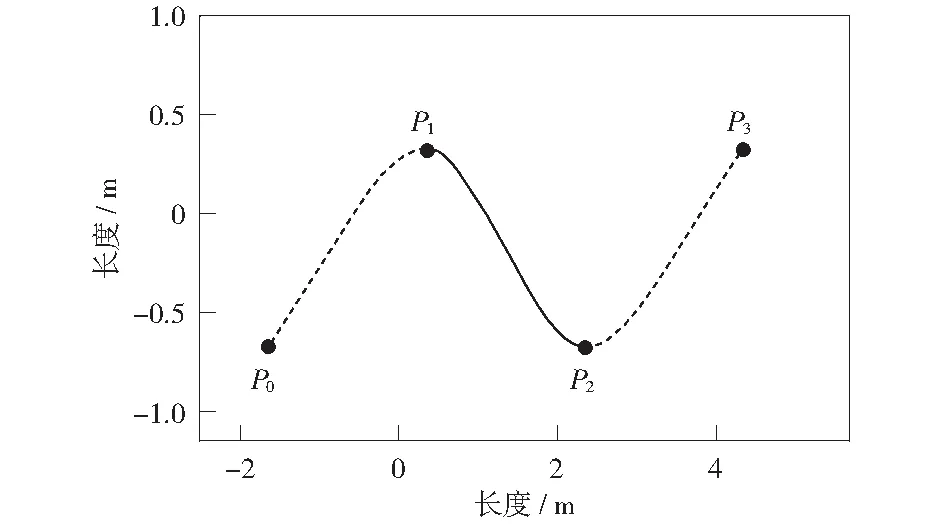
图4 Catmull-Rom曲线Fig.4 Catmull-Rom curve

(1)

式中，P(t)是指拟合出来的单段三次Catmull-Rom曲线，变量t的取值范围是[0,1].当t从0到1线性变化时，曲线就从P1点(t=0)移动到P2点(t=1)，生成P1和P2之间的曲线段。将式(1)转换为多项式形式，如式(2)所示。

(2)

式中：

在Catmull-Rom曲线中，首尾控制点P0和P3只是作为曲线拟合的辅助点，算法只会生成P1到P2之间的曲线段。如果需要曲线生成P0到P3的曲线段，则需要构造新的辅助点，例如可以使用[2P0-P1,P0,P1,P2]来绘制P0和P1之间的曲线，使用[P1,P2,P3,2P3-P2]来绘制P2和P3之间的曲线。

2.6 基于关键点的管线路径调整

采用Catmull-Rom曲线对规划路径进行曲线拟合后，可能会与其他物体发生干涉或不满足某些约束条件，这时可以通过自动或手动调整关键点的位置进行管线路径的适应性调整。

对于Catmull-Rom曲线，改变某个关键点的位置对该点相邻的曲线段有直接影响，对其他曲线段的影响很小。如图5所示，当曲线上点P3移动到P'3的位置时，只有P2，P3间和P3，P4间的曲线段发生明显变化。这一特点正是可弯曲管线路径规划设计所需要的，在不影响已完成的管线段的情况下，改变需要调整的管线段，保证路径规划的连续性。

2.7 最小弯曲半径约束

对可弯曲管线进行路径规划设计时，必须考虑最小弯曲半径的约束条件，对不满足该约束的管线段进行优化调整。管线路径的曲率半径计算方法[17]如公式(3)所示。

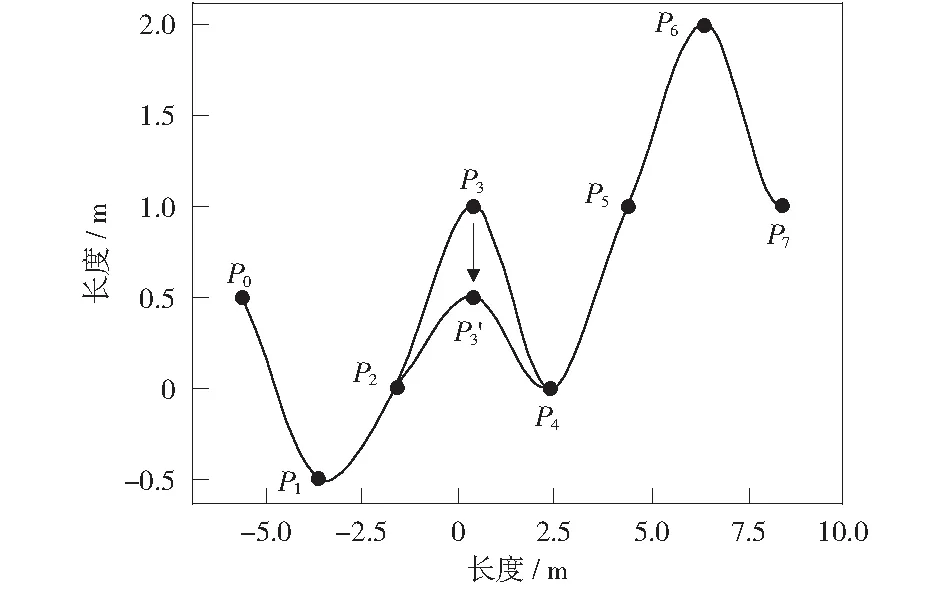
图5 调整路径关键点Fig.5 Adjust path key points

式中：r为管线的弯曲半径；P'和P"分别为P(t)关于自变量t的一阶导数和二阶导数。将曲线P(t)展开得到x，y，z三个方向关于自变量t的函数x(t)，y(t)，z(t)；x'(t)，x"(t)，y'(t)，y"(t)，z'(t)，z"(t)分别是分量x(t)，y(t)，z(t)关于自变量t的一阶导数和二阶导数。

计算管线路径上各个点的曲率半径，判断是否满足最小弯曲半径的要求。对不满足弯曲半径约束的路段，可以通过移动关键点位置或者增加、减少关键点的方式进行调整。

3 建模仿真

为了更加形象、直观地展示管线路径规划结果，在Unity场景下引入动态建模方法，结合路径中心线与管线单元模型生成实体管线模型。

3.1 管线建模

本文采用将管线路径和管线单元模型结合的建模方法，根据改进RRT算法和平滑处理后获得管线路径关键点；通过Catmull-Rom获得管线走线路径后，将管线单元模型顺次拼接得到完整的管线三维实体模型。管线单元模型如图6所示。

图6 管线单元模型Fig.6 Pipeline unit model

首先获取单元模型的三角面顶点信息，计算模型长度。三角面顶点信息包括顶点坐标、法线向量、纹理坐标和切线向量。然后根据管线路径的长度和方向，依次计算所有分段的三角面信息。根据单元模型三角面顶点信息和管线路径走向，将所有分段顺次拼接，同时去除位置相同的顶点，实现各分段的无缝链接，得到网格状三维管线模型。图7表示将单元模型按照管线路径方向顺次拼接、去除位置相同的顶点，虚线段之间为一个单元模型。

图7 单元模型合成管线模型Fig.7 Unit model synthesis pipeline model

3.2 实验仿真

本文所述RRT算法实验平台为Python3引入的matplotlib环境和Unity物理引擎。

3.2.1 基本RRT算法

图8(a)和图8(b)是用基本RRT算法在障碍物位置和数量一样、起点和终点相同的情况下，实验两次搜索出来的两条路径。在这种情况下，两条路径差别很大，存在路径搜索分散、耗时长、误差大等问题。

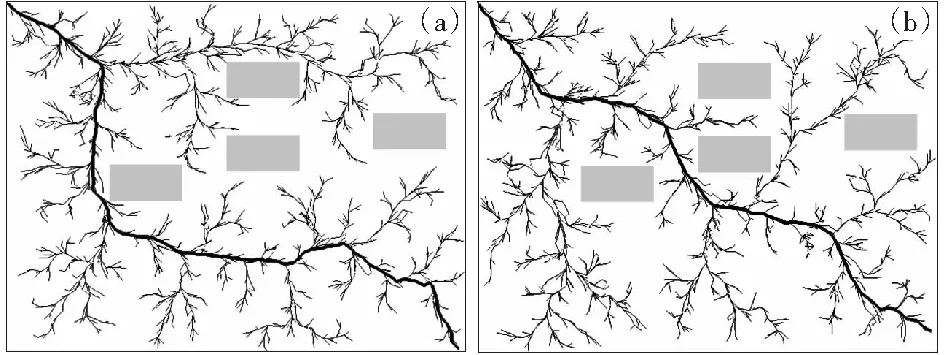
图8 基本RRT实验结果Fig.8 Results of basic RRT

3.2.2 节点扩展优化

在基本RRT算法的基础上，引入路径缓存的思想，增加随机节点为目标节点的概率。图9所示为连续6次规划得到的路径，6条路径在走向上大体一致，且路径更加平缓。

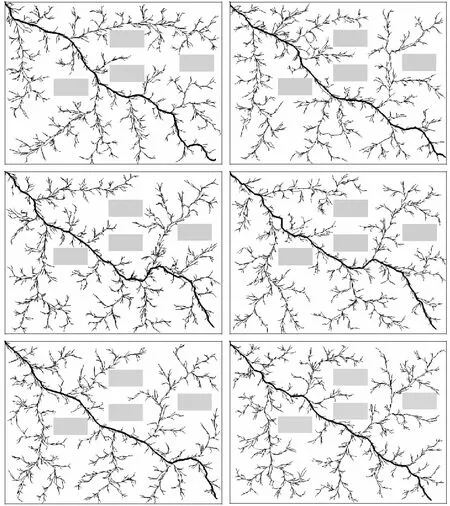
图9 节点扩展优化实验结果Fig.9 Results of node expansion optimization

3.2.3 路径平滑处理

基于RRT算法得到的初始路径包含大量的冗余节点。采用贪心算法删除这些节点，能够有效缩短管线路径长度，同时使路径更平滑，如图10所示。其中，折线为平滑后的路径。

图10 路径平滑处理实验结果Fig.10 Result of path smoothing experiment

3.2.4 双向快速扩展随机树

在单棵随机树的基础上，增加一棵从终点开始生长的扩展随机树。图11所示为三维环境下，基本RRT和双向RRT的对比实验结果。可以发现，在相同实验环境下，双向RRT在节点扩展和搜索效率上比基本RRT更优。

3.2.5 基于关键点的曲线拟合

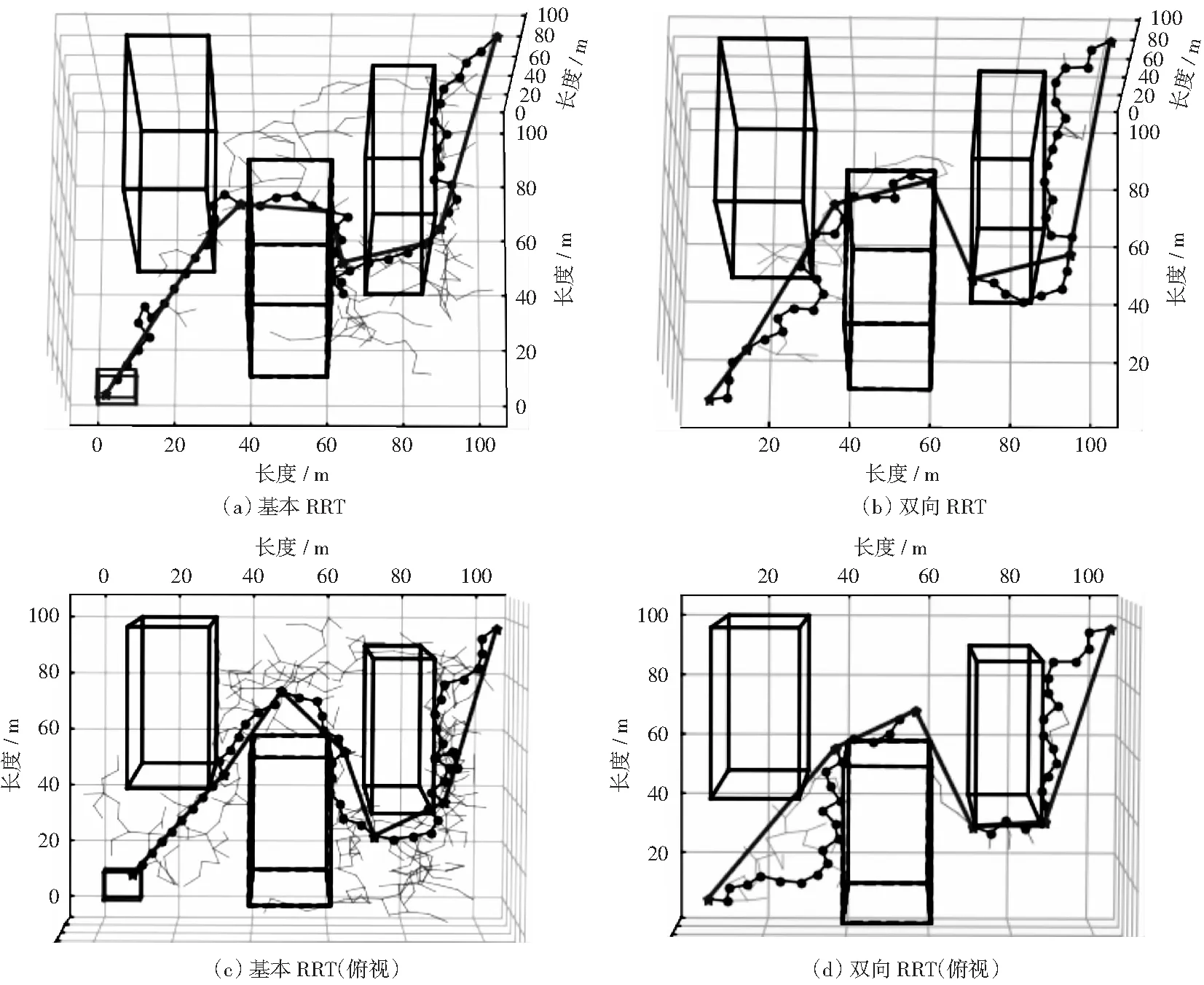
图11 基本RRT和双向RRT管线路径规划实验Fig.11 Basic RRT and Bi-RRT pipeline path planning experiments

经过平滑处理后的管线路径，虽然减少了关键点的数量，缩短了路径长度，但是在关键点处的折线路径可能无法满足某些管线的敷设要求，因此需要使用样条曲线拟合。本文采用Catmull-Rom曲线对关键点进行曲线拟合，拟合效果如图12所示。其中图12(a)和图12(b)为二维实验图，图(c)和图(d)为三维实验图，折线为平滑处理后的路径，曲线为拟合处理后的路径。

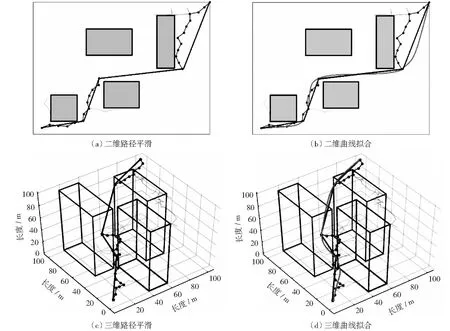
图12 管线路径曲线拟合实验结果Fig.12 Pipeline path curve fitting experiment

3.2.6 仿真实验对比分析

本文在Python环境下，采用同样的地图场景和A*算法、遗传算法进行对比实验，验证所提出算法的优越性和适应性。

图13表示本文方法在同一场景下迭代60次得到的路径长度。其中纵坐标表示路径长度，横坐标表示迭代次数。从图中可以看出，在引入路径缓存的情况下，本文算法能够快速收敛并稳定到一个较优的长度。

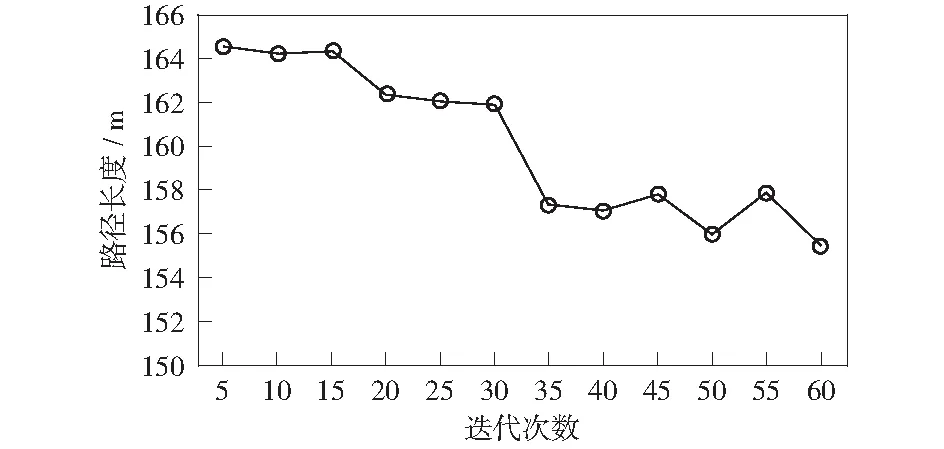
图13 进行60次迭代得到的路径长度Fig.13 Path length obtained from 60 iterations

在实验中，如果程序结束能够找到一条从始至终的路径，表示这次规划是成功的。表1所示实验结果为本文方法与A*算法、遗传算法在同一场景下进行50次实验得到的结果。可以看出，各算法均有很高的成功率，相比于A*算法和遗传算法，本文方法能够在更短的搜索时间内找到一条长度更短的路径。

表1 相同实验环境下三种算法实验结果Table 1 Results of three algorithess under the same experimental environment

3.2.7 Unity场景实验

在Unity平台上进行虚拟环境下的管线路径仿真模拟。图14表示经过搜索算法和关键点优化后得到的曲线路径。

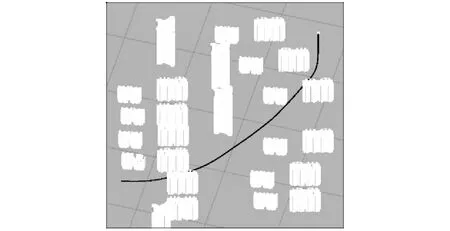
图14 管线路径规划与仿真建模Fig.14 Pipeline path planning and simulation modeling

4 结束语

本文在双向快速扩展随机树的基础上，引入路径缓存的方法，使扩展树的生长更具有方向性、高效性。采用贪心算法对管线初始路径进行平滑处理。利用Catmull-Rom曲线进行路径关键点的曲线拟合和调整，同时添加弯曲半径约束，使得管线路径更加合理、有效。

根据上述方法，本文设计实现了在Unity虚拟环境中进行管线路径规划，在规划路径的同时，进行三维管线实体仿真建模，实现管线的局部调整，使系统更加灵活。

本文方法适用于结构相对规则的管线、轨道类的路径规划设计和模拟仿真，在动态环境下的路径搜索和仿真还需要进一步研究。