基于局部自动编码器的手写数字分类
2018-11-15卢海峰陆慧娟
卢海峰,卫 伟,陆慧娟
(中国计量大学 信息工程学院,杭州 310018)
1 引 言
黄广斌等在2006年提出的超限学习机(Extreme Learning Machine,ELM)在分类和回归问题上具有泛化性能好、分类精度高、训练速度快等优点[1].然而随机初始化的特性正是其缺点所在[2],即输入权值和阈值的随机初始化导致了模型性能的不稳定性.文献[3]将受限玻尔兹曼机与ELM将结合,在对数据降维的同时,得到了ELM的输入权值和阈值.文献[4,5]分析了初始化不同的参数对ELM性能的影响:文献[4]针对输入权值的不同分布进行了研究,文献[5]针对输入权值和阈值的方差进行了研究.当训练样本参与到输入权值的初始化过程时,ELM分类精度得到了明显的提高[6,7],但它们都只是简单地组合训练样本,并没有充分提取和表达训练样本集的特征.文献[8]将训练样本先经过自动编码器(auto-encoder,AE),再将其输出权值用于ELM输入权值的初始化,并提出了基于AE逐层提取特征的方法.文献[9]提出了类限制超限学习机(class-constrained extreme learning machine,C2ELM),算法将训练数据按类通过AE进行训练,大大降低了计算过程中的使用内存,在一定程度上也提高了分类精度.输入权值的稀疏性可以进一步提高模型的性能,文献[10]将图像的局部区域作为输入权值的初始化,提出了局部感知的ELM.本文从文献[9,10]得到灵感,首先结合权值的稀疏性和分类训练的方法提出了基于局部自动编码器(local auto-encoders,LAE)的类限制超限学习机(receptive field class-constrained extreme learning machine,RF-C2ELM),然后比较ELM-AE(Extreme Learning Machine Auto Encoder)、C2ELM和RF-C2ELM在不同隐层结点数下的训练时间,接着将C2ELM和RF-C2ELM扩展为多层神经网络,并与ML-ELM(Multi Layer Extreme Learning Machine)作比较.
2 相关知识
2.1 ELM
对于任意N个互不相同的训练样本与对应标签的集合,数据组织形式为(xi,ti),其中xi=[xi1,xi2,…,xin]T∈Rn是模型的输入,ti=[ti1,ti2,…,tim]T∈Rm是整个模型的期望输出,i=1,2,…,N.假设SLFNs(Single-hidden layer feedforward neural networks)具有K个隐层结点,模型可以表示成:
(1)
其中oi=[oi1,oi2,…,oim]T∈Rm为模型的实际输出,ωi=[ωi1,ωi2,…,ωiK]T∈RK为连接输入层和隐层的权值向量,βi=[βi1,βi2,…,βim]T∈Rm为连接隐层和输出层的权值向量,bi为第i个隐层结点的阈值,f(·)为隐层的激活函数,通常选择sigmoid函数作为激活函数,ωi·xj表示ωi和xj的内积.如果具有K个隐层结点的SLFNs能以零误差逼近样本,(1)式可以简化成:
Hβ=T
(2)
其中
(3)
于是有:
(4)
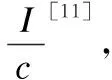
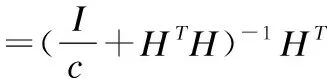
(5)
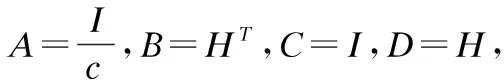
(A+BCD)-1=A-1B(C-1+DA-1B-1)-1
(6)
得到:
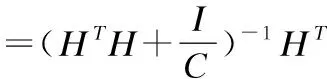
(7)
(8)
其中I为单位矩阵,C为正则化因子.
2.2 AE
AE最早由Rumelhart于1986年提出[13],其主要目的是对于一给定的数据集学习压缩的或分布式的特征表达[14].AE是一种典型的单隐层前馈神经网络,其期望输出恰好等于输入,即T=X.训练AE的方法主要有向后传播算法(BP)和基于ELM的方法[8].前者通过逐步迭代来不断修改网络参数,后者则是随机初始化输入权值和阈值,通过最小二乘法[15]计算得到输出权值.后者具有精度高、训练时间短等优点,因此本文采用该方法表达输入数据的特征.计算其输出权值的表达式式(9)所示.
(9)
2.3 C2ELM
C2ELM与ELM-AE的不同之处是:C2ELM先将训练样本按标签进行划分,再将每类训练数据通过AE,得到的输出矩阵初始化为ELM输入权值的某个分块矩阵[9];ELM-AE则是将所有训练数据通过AE,得到的输出矩阵初始化为ELM的整个输入权值矩阵[8].
虽然C2ELM的分类精度只比ELM-AE高出一点,但其训练时间远小于ELM-AE.原因在于对类别样本数据进行自动编码时,大大降低了内存的使用,从而加快了AE的过程.
2.4 ML-ELM
ML-ELM将ELM-AE进行堆叠,构造了一个多层神经网络[8].ML-ELM的构造过程如下:先将原始训练样本通过AE,把输出权值初始化为第一层的连接权值,然后把第二层神经元的输出信息通过AE,把计算得到的输出权值初始化为第二层连接权值,以此类推,直到构建完只剩最后一层连接权值为止,最后一层的连接权值可由式(8)得到.第j层神经元的输出可用式(10)表示:
Hj=g((βj)THj-1)
(10)
其中j≥1,训练样本输入X可看成是第0层输出H0.此外,训练每层连接权值的AE的输入权值和阈值是正交的,即满足:
aTa=I,bTb=1
(11)
其中a=[a1,…,ak]为正交随机输入权值,b=[b1,…,bk]为正交隐层阈值.
3 RF-C2ELM
在ELM中,稀疏的输入权值可以有效提高模型的预测精度.在手写数字分类中,文献[10]采用随机选取图像矩形区域来初始化ELM的输入权值,控制矩形区域内的图像信息保持不变,区域外的图像信息全部置0.输入权值ω1=[ω1,ω2,…,ωk]T的每一行ωi向量都是每个隐层结点选取图像矩形块后将区域外的信息置0再转换成行向量的结果.但是,将原始的图像信息初始化为输入权值并不能很好地表达该类数据的特征.因此,本节介绍一种基于LAE的类限制超限学习机.
3.1 算法描述
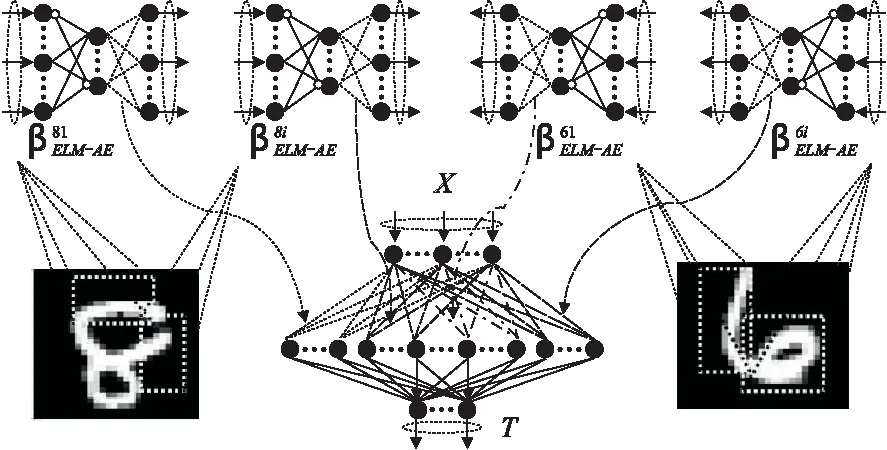
图1 RF-C2ELM结构示意图
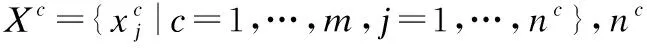
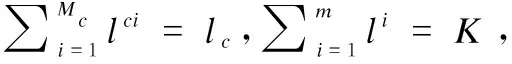
(12)
RF-C2ELM结构示意图如图1所示.
算法过程描述如下:
输入:训练样本{(xi,ti)|i=1,…,N},ELM隐层结点数K.
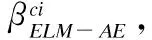
Step1. 标准化训练样本,在-1到1之间按均匀分布随机初始化隐层结点的阈值b,T=Ø.
Step2. 根据隐层结点数K为每类的每个AE随机选择矩形域集合T,按面积比例分配隐层结点数.
Step3. 对于每个矩形域,从所有输入样本中获得属于该类的样本xc,根据矩形域的范围将域外的数据置0.
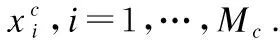
Step5. 利用公式(9)得到AE的输出权值βELM-AE.
Step6. 利用公式(12)合并ELM的输入权值WELM.
Step7. 利用公式(3)计算ELM的输出矩阵H.
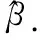
3.2 时间复杂度的比较与分析
为了突出ELM-AE、C2ELM和RF-C2ELM三种算法在训练时间上的差异,这一小节比较三种算法在初始化ELM输入权值上的时间复杂度.
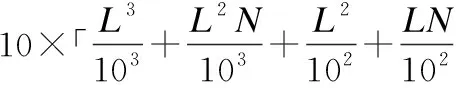
4 多层ELM
为了验证所提出的RF-C2ELM是否较好地提取了训练样本的特征,这一节将C2ELM与RF-C2ELM都扩展为多层ELM,并连同ML-ELM作预测性能的比较.
为了使图像分类精度更高,不同算法的实现在某些细节上存在着差异,比如AE输入权值和阈值是否正交和ELM第一层输出是否增加阈值.具体差异详见表1.
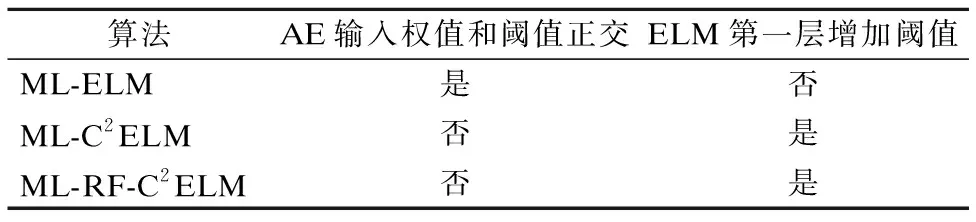
表1 三种算法在实现上的差异
另外,C2ELM并不是完全按类训练数据,而是附加了一个所有训练样本参与计算的权值[9],而ML-C2ELM与ML-RF-C2ELM则是完全按类训练数据,直接将每类训练样本交给单个或多个AE训练,从而在最大内存占用率和训练时间上获得更多性能的提升.
5 实验结果
实验执行的环境是windows 7操作系统上的MATLAB R2010b,计算机内核i5-6500@3.2GHz,内存8G.
MNIST手写数字集是测试ELM最常用的数据集.MNIST由60000个训练样本和10000个测试样本组成,每个样本的输入数据由784个像素组成,共10类.
图2是单隐层ELM在MNIST测试集上的误差率.从图中不难看出,ELM-AE、C2ELM和RF-C2ELM的误差率远小于随机初始化参数的ELM,而且RF-C2ELM的误差率明显小于ELM-AE和C2ELM,说明该算法在浅层(即三层)神经网络下提取到了更好的特征.
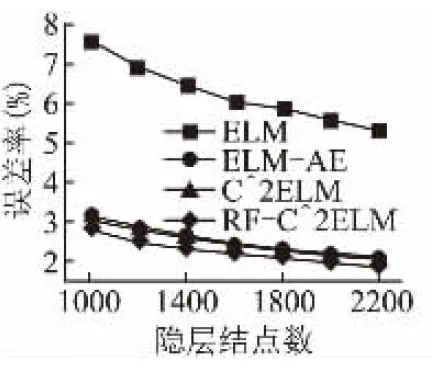
图2 网络结构为“784-?-10”的测试集误差
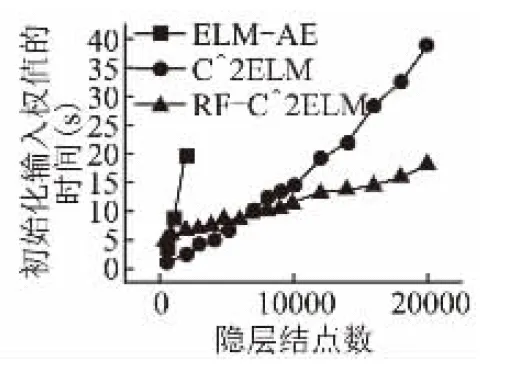
图3 单隐层输入权值的训练时间随隐层结点数的变化
为了验证优化的第一层连接权值是否能有效逐层传递特征,下文将重点放在多层ELM上.接下来的实验以4层神经网络为例,即双隐层前馈神经网络,其中输入层结点数为784,第二层结点数固定为700,第三层结点数可调,输出层结点数为10.网络结构可表示为784-700-?-10,“?”表示该层结点数可调.图3记录了训练输入权值的时间随隐层结点数的变化.我们可以得到以下结论:RF-C2ELM初始化ELM输入权值的时间基数较大,但随隐层结点增长的速度较慢.当隐层结点数较少时,RF-C2ELM的训练时间较长,但当隐层结点数大约超过7000时,RF-C2ELM则是三种算法中效率最高的.由于单台计算机内存有限,为了使可调的结点数达到更高的上限,在多层ELM上采用在线序列学习[17]的方式,将数据分批训练,可调结点数最高可达6000.MNIST测试集与训练集在784-700-?-10结构下的误差率分别如图4和图5所示.
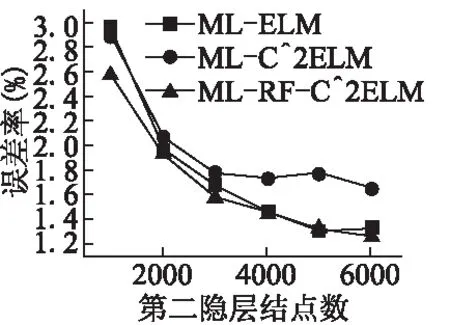
图4 网络结构为“784-700-?-10”下的测试误差率
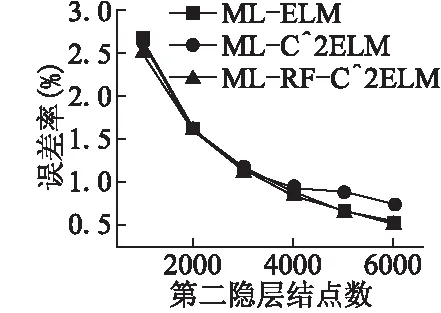
图5 网络结构为“784-700-?-10”下的训练误差率
表2列出了三种算法在网络结构为“784-700-6000-10”下的测试集误差率,表中Ri表示初始化第i层连接权值的AE的正则化因子,其中i∈{1,2},R3表示计算ELM输出权值的正则化因子.从图表可以看出ML-RF-C2ELM的预测精度最高,说明该算法能有效提取特征并进行特征逐层传递.
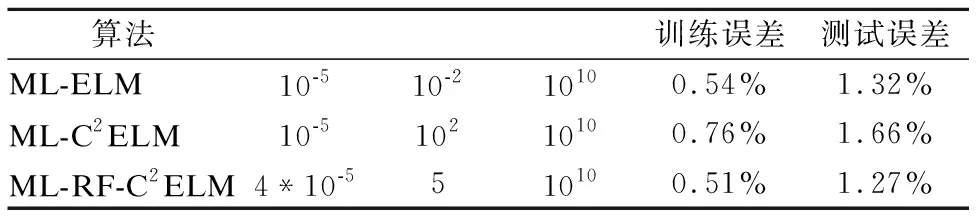
表2 网络结构为“784-700-6000-10”下的测试误差率
6 结 语
本文提出了一种基于LAE的类限制ELM,将其同C2ELM一起扩展到多层神经网络,目的是为了验证该方法的特征提取能力和逐层传递能力.实验结果表明,ML-RF-C2ELM在图像分类问题上能保持较高的预测精度.
