基于凸包的最小有向包围盒生成算法
2018-11-15秦启飞胡志刚
秦启飞,胡志刚
(中南大学 软件学院,长沙 410075)
1 引 言
物体的包围盒广泛应用于图像处理、模式识别、碰撞检测、模具分型设计和机械控制等领域[1,2].目前应用最广泛的OBB(Oriented Bounding Box,有向包围盒)根据物体本身的几何形状来决定包围盒的大小和方向,可以对原模型进行紧凑的拟合[3].对于给定的三维点集,怎样高效而准确地得到其最小有向包围盒一直是国内外学者关注的问题[4].
一般考虑物体的所有顶点在空间的分布,通过不同的算法找到最佳方向,以确定OBB包围盒的几个轴.主要使用数值和统计优化方法来找到非最优,但在实际使用中足够好的近似值.目前的主流方法是使用主成分分析(PCA)[5],根据物体表面的顶点,计算特征向量来估计点集中最大扩展的方向,并作为OBB的主轴.这个过程必须使用凸包上的连续集合表示来完成,否则近似值可能是无界差的[5].为了获得接近最优的结果,Barequet and HarPeled提出一个(1 +α)逼近方案[6],而另一方面,Larsson和 Kallberg则提出可以采用预定义的启发式方法来获得更好的计算速度[7].国内的陈柏松等[4]提出了基于非线性主成分分析的最小包围盒计算方法,在计算时间和运行结果上都取得了不错的效果,但是该方法利用了顶点之间的连接信息,无法处理无连接关系的点集数据.
还有学者提出使用粒子群优化[8]和遗传算法[9]来计算最佳结果,取得了不错的效果.但这些算法中包含随机因子,不能保证在所有情况下都找到最佳包围盒.
法国的Chang等提出混合包围盒旋转识别算法HYBBRID,采用遗传搜索方法对SO(3,)的所有方向的进行暴力搜索[10].对于给定OBB的候选方向,将模型重复地投影到与当前候选OBB的主轴相对应的平面上,将其转化为2D问题,使用Toussaint的旋转卡尺方法[11]在线性时间内进行求解.这减少了暴力搜索的难度,将问题转化为在单位半球中搜索较优的起始方向向量.通过不断重复计算得到最佳OBB的取向.然而,在该方法中搜索是在连续的空间上进行的,不能通过对一组离散的取向进行采样.
综合上述分析,已知的使用近似值,数值计算或启发式方法的算法,效果都不够出色.本文提出一种快速准确的几何算法来解决该问题.首先对三维点集的凸包进行分析,总结了凸包和其最小体积有向包围盒的4种边面接触类型.通过枚举凸包所有边可能的组合,选取包围盒的最优方向.实验证明,该算法可以快速生成符合模型体积特征的最小有向包围盒,且拟合效果良好.
2 问题定义
2.1 问题描述
由于模型内部的点对问题的解决没有任何帮助,所以本研究基于凸包的边上进行操作.可以使用Quick Hull算法[12]或其改进方法[13,14]在O(n log n)时间复杂度内计算点集的凸包.
最小有向包围盒生成问题定义如下:
输入:三维点集构成的凸包顶点集V
输出:最小有向包围盒O
2.2 相关符号与概念
为了更好地进行后续讨论,首先对相关符号和概念进行介绍:
定义1.支持顶点 (Supporting Vertices).在凸包中,方向向量n的方向上的一个或多个最高顶点,成为支持顶点,表示为Supp(n).
定义2.对向(Antipodal).对于两个顶点v1和v2,如果存在一个方向向量n,使得v1∈Supp(n)和v2∈Supp(-n),则称v1和v2的位置关系为对向.其几何描述为:如果可以找到封闭OBB的某个方向,使得凸包上的两个顶点位于OBB的相对面上,则该两个顶点是对向的.
定义3.侧向(Sidepodal).对于两个顶点v1和v2,如果存在两个方向向量n1和n2,使得v1∈Supp(n1),v2∈Supp(n2),并且n1·n2=0,则称v1和v2互为侧向.其几何含义是,对于一个闭合的OBB,如果可以找到一个方向使得顶点v1和v2位于该OBB相邻的两个相邻面上,则称v1和v2互为侧向.
支持,对向和侧向的概念同样可以用来表示凸包的的边和面的关系.如果一条边e和顶点v分别位于该OBB的两个相邻面,那么也称边e和顶点v相互侧向.
如果x是凸包的顶点或边,则凸包中x的所有对向顶点的集合将表示为AntiV(x),凸包中x的所有对向边的集合表示为AntiE(x).同样,SideV(x)和SideE(x)表示x所有侧向的顶点和边的集合.此外,对于上述的侧向集合, SideV(e1,e2)表示集合的交集SideV(e1)∩ SideV(e2)的简写.显然,如果一条边e:v1→v2,是特征x的对向边或侧向边,那么边e上的顶点v1和v2也具有相同的性质.即:
如果:e∈AntiE(x),那么:{v0,v1}∈AntiV(x),
如果:e∈SideE(x),那么:{v0,v1}∈SideV(x),
如果:e∈SideE(x1;x2),那么:{v0,v1}∈SideV(x1,x2).
因此,遍历对向边集或侧向边集,等效为遍历其顶点的集合.值得注意的是,对于侧向关系,反过来则不成立.即使两个相邻的顶点对于特征x是侧向的,连接它们的边却不一定也与x侧向.
符号N(v)表示顶点v的邻居顶点集合.从凸包内部测量的连接边e的两个相邻面之间的角度通常称为边e的二面角(Dihedral Angle).因为凸包是凸形,所以所有的二面角的范围都在(0,180)内.最后,在边e两侧指向凸包外侧的两个相邻面的法线表示为f<(e)和f>(e).这些法向量具有以下属性:
引理:如果OBB的面与凸包的边e齐平,那么OBB的该面的(非归一化的)法向量n为:
n=f<(e)+(f>(e)-f<(e))*t,t[0,1]
证明:该公式直接来自线性插值.t=0的值对应于OBB与法向量f(e)的面齐平的情况,t=1的值对应于与法向量f>(e)的面齐平的OBB.由于边的二面角从不为0,所以线性内插值不会产生简并零向量.
实际上,我们可以使用几何的方法将凸包的顶点和边与支持函数相关联.
引理:给定凸包的一个顶点v和一条边e,当且仅当存在一个方向向量n使得v∈Supp(n)且(n·f<(e))(n·f>(e))≤0时,顶点v∈Sidev(e).
证明:根据引理,与边e齐平的OBB的面的法向量n2具有性质:
n=f<(e)+(f>(e)-f<(e))*t.当且仅当存在向量n使得v∈Supp(n)和n·n2=0时,顶点v与边e侧向.将法向量进行替换,给出下列公式:
n·(f<(e)+(f>(e)-f<(e))*t)=0,t[0,1]
(1)
公式左侧是关于t的线性表达式,所以当t取0和1时,表达式取得极限值,分别为:n·f<(e)和n·f<(e).因此,当且仅当n·f<(e)和n·f<(e)中一个为正数,一个为负数时,该方程有解.即:
n·f<(e)≤0,且n·f<(e)≥0,
或者n·f<(e)≥0,且n·f<(e)≤0.
无论哪种情况,将两个表达式相乘就可以得到引理.
对于凸包的顶点和边,不论是对向还是侧向,都是非传递的关系.本文将通过对凸包的顶点图进行计算来得到相关关系,具体的实现算法在2.3节给出.
2.3 对向和侧向关系判断算法
基于2.2的论述,给出以下判断顶点与边和两条边是否为对向关系的算法:

图1 算法AreAntipodal(v,e)
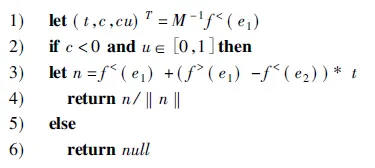
图2 算法AntipodalDir(e1,e2)
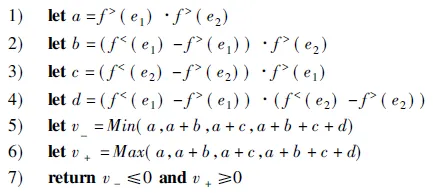
图3 算法AreSidepodal(e1,e2)
图1中算法输入为:顶点v,边e;输出为:顶点和边是否是对向关系.图2中算法输入为:凸包的两条边e1,e2,输出为:使得两条满足对向关系的单位向量.
同样,可以使用图三中算法来判断两条边是否为侧向关系.图3中算法输入为:凸包的边e1,e2;输出为:两条边是否是侧向关系.
3 最小有向包围盒生成算法
3.1 凸包与其OBB的4种接触类别
该算法总体策略是:通过计算通过凸包边的组合唯一确定OBB方向,而不是对球体中的所有可能定向方向进行暴力搜索.
Freeman和Shapira[11]提出并证明了,在二维情况下,图包的最小面积的包围矩形的一条边必定与凸包的一条边共线,因而考虑凸包的每条边,以此作为凸包的包围矩形的一条边.在三维情况下,通过对大量实例的分析,提出以下假设:
假设1:凸包至少有三条不同的边,与其最小体积OBB包围盒的表面共面,其中至少两条边位于OBB的相邻面上.
该假设意味着凸包的特定边e位于OBB的特定表面f上.基于上述假设,根据凸包及其封闭OBB的边缘接触不同情况,分为以下4个类别,与OBB接触的边以粗线条突出显示:
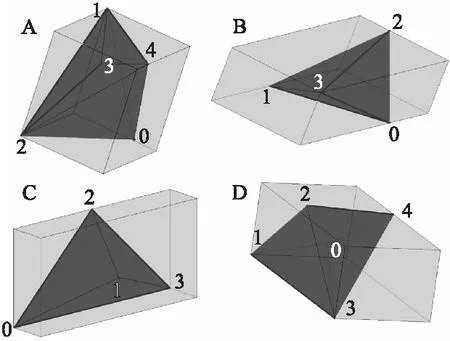
图4 凸包及其OBB的四种不同边缘接触示例
1)类别A:凸包三条边位于OBB的三个相互相邻的面.
该类别的实例如图2-A所示,其中顶点坐标为:
0:(1,0,2);1:(1,4,3);2:(4,0,4);3:(4,2,1);4:(3,2,0)
凸包的边1→2,1→4和2→3位于OBB的三个相互相邻的面,顶点0位于与边1→2所在平面相对的面上.
2)类别B:凸包三条边位于OBB的三个面,其中两个是对面.
该类别的实例如图2-B所示,其中顶点坐标为:
0:(0,2,0);1:(0,2,2);2:(0,4,0);3:(2,0,2)
凸包的边0→1,0→3和2→3位于OBB的三个面.其中,边0→1和2→3位于两个相对面.
3)类别C:凸包三条边位于OBB两个相邻的面.
凸包的三条边位于OBB的两个相邻面,即凸包的一个面和一条边与OBB重合.该类别的实例如图2-C所示,其中顶点坐标为:
0:(0,0,0);1:(5,2,2);2:(5,5,0);3:(10,0,0)
凸包的三条边位于顶点0→2→3形成的平面,顶点1位于该面的对面.需要注意的是,在上述示例中,相邻面的交边0→3,刚好位于凸包与OBB重合面,但这种情况不总是发生.
4)类别D:凸包两条边位于OBB三个面,其中两个是对面.
OBB的三个不同面上仅与凸包的两条边齐平.这是一种特殊情况,其中凸包的边与OBB的边重合.此时,OBB上必须存在两个包含凸包边的对向面,否则将包围盒和凸包沿公共共享边投影到2D平面(将共享边缩减至一点)时,所得2D矩形没有与所得2D多边形的任何边重合,因此不是最优解.该类别的实例如图2-D所示,其中顶点坐标为:
0:(0,4,2);1:(0,4,4);2:(2,4,2);3:(3,0,1);4:(1,4,0)
在该示例中,最小体积OBB仅与凸包的两条边齐平,但是这些边位于OBB的三个不同的面.顶点0是不与OBB接触的内部顶点.
3.2 搜索最小封闭OBB包围盒
通过搜索测试图2所示的每种类别情况:
1)对于类别A和类别B:
对凸包中每条边e1∈E进行遍历,寻找可能位于OBB的相邻侧面上的所有边e2∈SideE(e1).然后,针对类别A,搜索OBB中与先前两个面相互相邻的第三个面上的所有边e3∈SideE(e1,e2).对于类别B,搜索OBB中与边e1接触的面相对的第三面上的所有边e3∈AntiE(e1).
2)对于类别C:
对凸包中面f∈F进行遍历.确定OBB的一个面法线n1.对边集F中任意一边e1,遍历e3∈SideE(e1).
3)类别D:
类别D可以看作类别B中e1=e2时的特殊情况,因此在搜索类别B时隐式处理此类别,因此不需要单独进行测试.其几何含义时,边可能和自身是侧向的.
执行上述迭代的过程如图5所示.

图5 算法FindMinOBB(V,F ,E)
算法伪码包含几个中间过程函数.函数ComputeBasis(e1,e2,e3)和函数CompleteBasis(n1,e)是两个空间几何计算函数,作用是通过3条边或者1条边和1个向量建立包围盒的基底.函数ComputeOBB计算凸包的六个极端顶点,分别对应OBB的每个面,为计算OBB的方向提供基础.使用Dobkin-Kirkpatrick层次数据结构,最多需要O(log n)时间.函数RecordOBB是常数时间的计算,它计算新创建OBB的体积,与之前的记录的OBB进行比较,并存储两者中较小的一个.
算法中输入为:凸包顶点集V,表面集F,边集E;输出为:最小包围盒OBB.算法包含两个单独的顶级循环.第一个用(行1-行13)来处理类别A,B和D,第二个循环(行14-行21)处理类别C.在第一个循环结构中,外层循环(行1-行13)确定凸包的一条边,这是一个O(n)的操作.第二层循环(行2-行13)遍历第一条边的所有侧向边.时间复杂度为O(logn+|SideE(e1)|).
第一个最内圈循环(3行-7行)针对类别A的情况进行处理,时间复杂度为O(logn+|SideE(e1,e2)|).首先建立OBB的方向,对于给定的三条边,调用函数ComputeBasis计算基底(n1,n2,n3).然后,调用函数ComputeOBB和RecordOBB处理该基底.
第二个最内圈循环(行8-行13)针对分类B的情况进行处理,时间复杂度为:O(logn+|AntiE(e1)|).对满足条件的边进行迭代,首先使用算法2计算OBB一个面的法向量,通过函数ComputeBasis计算基底,然后调用函数ComputeOBB和RecordOBB完成计算.
最后,第二个顶级循环体(行14-行21)针对类别C进行遍历.凸包中每个面都可以直接确定一个法向量.内圈循环(行17-行21)时间复杂度为:O(logn+|SideE(e1)|),对边e1的对向边集进行遍历,为OBB的第二个轴的确定一个候选方向,以完成后续计算.
第一循环结构中的步骤总数为:
|E|(logn+|SideE(e*)|)(logn+|SideE(e*,e*)|+|AntiE(e*)|)logn
第二个循环为|F|(logn+|SideE(e*)|)logn.在标准球型Sphere(n)数据集上,算法运行时间是O(n3/2(logn)2).在最坏的情况下2,如在圆柱型Cylinder(n)数据集的情况下,算法运行在O(n3logn)时间.
4 实验分析
4.1 实验数据
本文进行了大量的实验来测试算法的拟合效果和执行效率.实验使用C++编程语言和开源软件包MathGeoLib[15]实现,所有实验均运行于Dell T700 型号PC机器,处理器为Intel Core i7 3.6GHz,内存为16GB,操作系统为Windows 10专业版.测试程序使用Microsoft Visual Studio 2017编译器构建,采用64位编译,所有基准测试中均为单线程执行.
实验选用两个不同的数据集进行验证,分别为:1.标准球体数据Sphere(n),n表示凸包中顶点数量,模型通过程序自动生成.2.GAMMA Group 3D网格研究数据库[16],包含5个不同的类别的数据集,共计2088种不同的3D模型,包括:
·来自数据集2001的55个模型.
·来自数据集ANIMALS.的381个模型.
·来自数据集ARCHITEC的530个模型.
·来自数据集GEOMETRY.的437个模型.
·来自数据集MECHANICAL的685个模型.
4.2 实验结果分析
对于标准球型数据集Sphere(n),首先采用Quick Hull算法计算凸包顶点,然后使用本文所述算法搜索其最小体积OBB包围盒,以下所有指标均不包括运行Quick Hull算法所需的时间.如图5所示,对于相同半径的球体,当凸包顶点数达到500时,已经可以较好地还原物体形状.而本文所述算法搜索到的最小体积封闭OBB包围盒,可以对所有的凸包进行紧密的包围,取得了良好的效果.
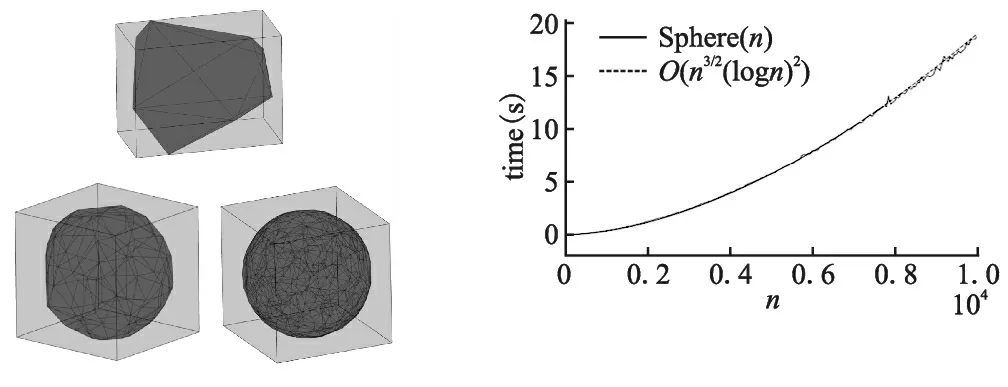
图6 Sphere(n)数据集OBB示例 图7 数据集Sphere(n) 中计算最小体积OBB耗时
算法运行时性能如图6所示,其中X轴表示数据凸包中顶点的数量,Y轴表示计算OBB所对应的时间,实际数据以细线绘制.结果表明,当凸包顶点数在10000以下时,算法表现与预期的O(n3/2(logn)2)性能回归曲线有较好的匹配.由于包围盒仅取决于模型的凸包,因此先将GAMMA Group真实模型数据集中的模型进行预处理.
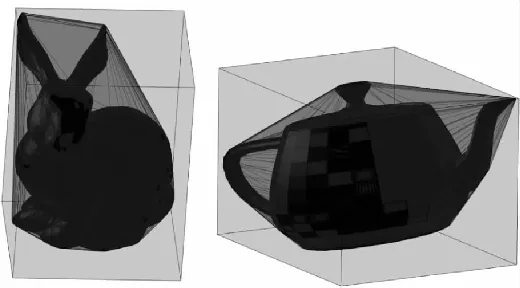
图8 GAMMA Group模型OBB示例
算法的拟合效果如图8所示,可以看出对复杂物体模型,算法所计算出的包围盒也可以进行非常紧密的包围.图9中散点图显示了算法的性能情况,X轴为该对象的凸包上的点数,Y轴表示计算OBB所需的时间(秒).这个基准测试的结果表明,大多数现实世界模型对象的计算性能与Sphere(n)的情况非常相似.如图9所示在参与测试的2088个模型中,大部分模型表现接近最佳预期.

图9 GAMMA Group数据集下计算最小体积OBB耗时
在GAMMA Group数据库的5个不同数据集中,分别对本文所提算法和文献[10]中的HYBBRID算法进行对比试验,包围效果如图10所示.因为模型个体形状差异较大,所以选取算法在不同数据集中最优、中等和最差各情况表现比较所得OBB包围盒与原模型的体积之比,比值越小表示可以更紧密的包围.其中Optimal、Median、Max为本文所提算法数据,与之对比的是HYBBRID Optimal、HYBBRID Median、HYBBRID Max 三个指标.从图中可以看出,本算法在最优情况下,包围效果与HYBBRID算法相同或者略优;在中位数情况下明显优于HYBBRID算法;在最坏情况下,表现比HYB-BRID算法略差.而从图11可以看出,在5个不同的数据集上,本算法的平均耗时均低于HYBBRID算法,具有更好的计算性能.
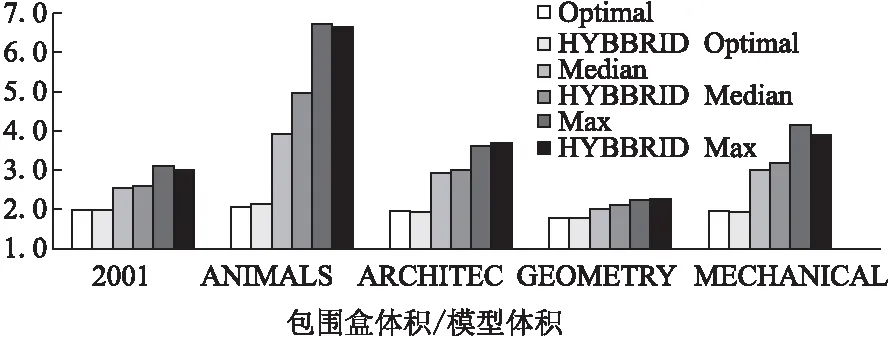
图10 与HYBBRID算法包围效果对比
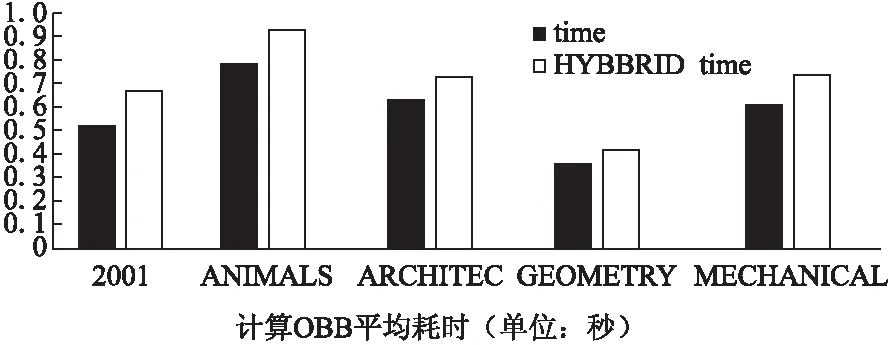
图11 与HYBBRID算法性能对比
5 总结与展望
本文首先对三维点集凸包中点线面关系进行分析,总结了凸包与其最小OBB包围盒的4种边面接触类型.并提出了一种计算三维点数据的最小定向包围盒的新算法,该方法首先针对输入点集构造凸包,通过快速迭代凸包边的组合,唯一确定OBB的最优方向.最后通过实验证明,该算法能够精确地找到所有模型的最小OBB包围盒,且具有更好的性能表现.
该算法是一个离散的过程,不使用连续统计的数值优化或迭代.因此,该方法是稳定和可预测的.同时,与以前公开的结果不同,该方法相对容易实现,并且可以以不同的方法对其进行编程,以平衡实现复杂度与运行时复杂度.
此外,因为算法在凸包的边集合上只读顺序遍历,它可以很容易被改写为并行算法,因此也适用于处理大数据集.
针对模型极端复杂的场景,该算法的包围效果还存在进一步优化空间.且该算法只适用于计算最小体积OBB包围盒,暂未考虑对于追求最小表面积的OBB包围盒场景.因此,后续研究可以就复杂模型的包围优化,以及针对最小表面积情况进行进一步探索.
