基于OpenMP的旋翼气动噪声并行计算

任明霞，杨爱明

(复旦大学 航空航天系，上海 200433)

相对于固定翼飞机，直升机因其独特的起降方式，在军用和民用领域得到了广泛的应用.但是直升机面临的一个重要问题就是噪声问题.在民用领域，该问题严重影响乘坐舒适性和地面环境；在军用领域，该问题严重影响直升机的隐身性能.旋翼噪声的精确数值预测方法作为低噪声旋翼优化设计的先导技术，无疑具有重要的工程应用价值.

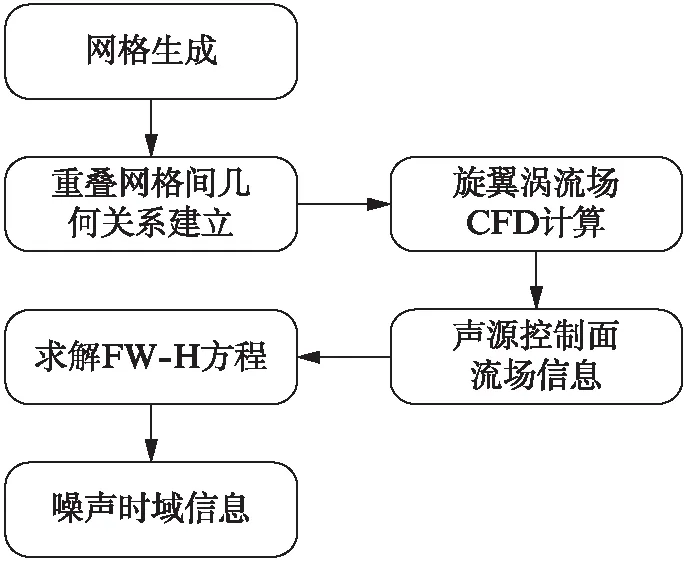
图1 旋翼噪声计算技术流程图Fig.1 Technology flowchart of rotor noise calculation

如果观测点距离直升机较近，直接利用计算流体动力学(Computational Fluid Dynamics, CFD)方法计算观测点处的噪声是可行的.但是对于远场噪声问题，观测点与直升机距离较远，直接应用CFD方法计算远场噪声问题是不现实的，其主要原因在于数值耗散和数值色散的影响.目前主流的噪声计算方法是一种将CFD与声比拟相结合的方法.在近场，通过数值方法求解Euler方程或Navier-Stokes(N-S)方程，得到声源控制面上的信息；在远场通过求解描述声波传播的波动方程得到远场的压力波动.Ffowcs Williams和Hawkings[1]于1969年在Lighthill声比拟研究的基础上，将N-S方程重新整理成非齐次波动方程的形式，得到了著名的FW-H方程.该方程可以描述运动物体产生的远场噪声问题，目前旋翼噪声的数值预测大多采用该方程.由于FW-H方程是一个微分方程，直接求解比较困难，NASA的科学家Farassat[2]提出了一种积分方法，得到了FW-H方程的两个求解公式，即F1和F1A.该积分方法甚至可以将声源面取为可穿透的控制面.本文对旋翼远场噪声的数值计算采用可穿透的控制面，通过F1A公式进行求解.

根据Farassat的积分公式求解FW-H方程，需要先得到直升机旋翼的流场信息，图1为旋翼噪声计算的技术路线示意图.在本文工作中，旋翼流场的数值计算采用格心格式的有限体积方法[3],时间推进采用双时间推进方法[4-5]，子迭代由LU-SSOR方法[6]完成.旋翼涡流场的CFD计算中，由于隐式LU-SSOR方法在每个迭代过程中占据主要的计算时间，因此对LU-SSOR算法进行并行计算无疑可以提高旋翼涡流场的计算效率，大大缩减程序运行时间.

并行编程是使用程序语言显式地进行说明，从而实现将计算任务中不同部分分配给不同的CPU同时执行.目前，工程技术人员常用的编程语言是消息传递接口[7](Message Passing Interface, MPI)和直接控制共享内存式并行编程的应用程序接口[8](Open Multi-Processing, OpenMP).MPI需要明确划分数据结构并重构源程序，编程困难且开发周期长，而OpenMP主要针对循环进行并行，能有效克服并行编程的可移植性和扩散性能差的缺点.基于此，本文选用OpenMP进行源程序的并行优化,针对隐式LU-SSOR算法存在较强数据依赖性的问题，发展了两种并行策略.

1 数值方法

1.1 流场计算方法

在绝对坐标系下，积分形式的RANS方程为：

(1)

式中：W为守恒变量；Hc和Hv为对流通量和粘性通量.表达式如下：

(2)

(3)

式(2)和(3)中：ρ，(u,v,w)，p，E，H，k，T和τ分别为流体密度，流体速度在3个坐标方向上的分量，压强，单位体积的总能，单位体积的总焓，热传导系数，温度和粘性应力；V和Vb分别为流体速度矢量和网格速度矢量.为了封闭方程，还需要引入如下的状态方程：

p=(γ-1)ρ[E-0.5(u2+v2+w2)].

(4)

在计算旋翼的悬停流场时，由于在旋转坐标系下观察流体的绝对运动，流动是定常的.因此将控制方程在旋转坐标系下表达无疑是方便的.引入如下公式：

(5)

式中：

B=Bxi+Byj+Bzk=Br=Bxrir+Byrjr+Bzrkr,

(6)

(7)

(i,j,k)和(ir,jr,kr)分别为绝对坐标系和旋转坐标系下的坐标轴方向单位矢量；ω为旋转坐标系相对于绝对坐标系的旋转角速度矢量.将式(5)应用于绝对坐标系下的控制方程(1)中的3个动量方程，则可以得到如下的旋转坐标系下的控制方程：

(8)

(9)

与绝对坐标系下的控制方程(1)相比，方程(8)中多了一项源项.方程(9)中各物理量的介绍在此省略.式(8)和(9)中，下标r代表旋转坐标系.值得指出的是，式(8)和(9)中所有矢量均为绝对矢量，仅对其分量在旋转坐标系下表达而已.

旋翼流场的数值计算采用格心格式的有限体积方法.对于任意控制体Vi,j,k，应用式(1)可得

(10)

(11)

式中：

(12)

1.2 时间推进

用二阶向后差分近似式(10)中的物理时间导数项可得

(13)

为了得到物理时间t上的时间精确解Wn+1，我们在式(13)中引入守恒变量对伪时间τ的导数项，则可以得到：

(14)

显然，伪时间方向上的定常收敛解即为物理时间上的时间精确解.为了方便起见，我们将待求变量Wn+1重新记为W*，则式(14)可改写为：

(15)

式(15)在伪时间方向上的时间推进格式采用隐式LU-SSOR方法.首先采用一阶向后差分近似伪时间导数项

(16)

然后将残值R进行线化处理(仅处理无粘部分)，即：

(17)

将式(17)代入式(16)，则可得到：

(18)

式中：A，B和C分别为3个方向上的Jacobian矩阵，即

交界面处的Jacobian矩阵按照如下的迎风格式处理：

(19)

其他方向依此类推.式(19)中A±的定义为：

式中：ρA为A的谱半径；σ为一个略大于1的常数；I为单位矩阵.上述定义可以保证A+的所有信息向正方向传播，而A-的所有信息向负方向传播.定义如下3个算子：

(20)

则式(18)可以写成如下的算子形式：

(L+D+U)ΔW*=RHS,

(21)

RHS由下式定义：

(22)

又因为

(L+D+U)ΔW*≈(L+D)D-1(U+D)ΔW*,

(23)

则我们可以得到如下的方程：

(L+D)D-1(U+D)ΔW*=RHS.

(24)

该方程的求解可以分为两步，即上扫和下扫过程：

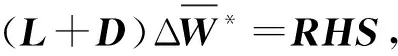
更新 (W*)m+1=(W*)m+1+ΔW*.

值得指出的是，为了提高计算效率，一般将伪时间步长取为无穷大，则子迭代过程近似为高效的Newton迭代.

2 OpenMP并行计算

由以上推导过程可知，LU-SSOR方法存在很强的数据依赖性，因此不能利用一般的OpenMP并行语句进行并行处理.基于此，本文根据NAS并行基准[9]发展了超平面(Hyperplane)和管道流(Pipelining)两种并行策略.

2.1 超平面策略

由于隐式LU-SSOR存在很强的数据依赖性，因此不能简单地在I/J/K任意一个方向上做OpenMP并行计算.超平面算法的思想是构造平面M=I+J+K，计算沿着构造平面进行，然后将任务在J方向上分配给不同的线程，实现并行计算.

以二维情况为例，如图2，超平面方法将计算空间划分为一个个的平面，M=I+J，然后在J方向上进行并行计算.实心圆为流场信息已知的网格点，空心圆为待求解流场信息的网格点.以点(Ia,Ja)为例，在用双时间算法进行推进过程中，点(Ia,Ja)的流场值依赖于点(Ia-1,Ja)和点(Ia,Ja-1).超平面算法可以保证点(Ia-1,Ja)和点(Ia,Ja-1)的流场值先于点(Ia,Ja)更新，从而解决了数据依赖性问题.即对于任意一个超平面L，其上的网格点数值仅仅与上一个超平面(L-1)上的网格点有关，超平面内的网格点之间没有数据依赖性.

2.2 管道流策略

管道流方法的核心思想是在最外层方向上(比如K方向)建造一条管道，在该管道内，每个线程相当于一个流水线.然后将里层(比如J方向)的任务静态地分解成许多子任务，并分配给相应的线程.

图2 超平面算法示意图Fig.2 Hyperplane algorithm schematic

图3 管道流算法示意图Fig.3 Pipelining algorithm schematic

图3给出了拥有n条线程(T0，T1，T2，…，Tn-1)或称管道流线的管道流算法示意图.在K方向上建造管道，使每个线程都将K的取值遍历一遍.对于第N层(K=N)，J方向上的任务被分成M份，并依次分配给n个不同的线程.因为存在数据依赖，任务队列中任务KNJM的执行需要在任务KN-1JM和KNJM-1之后.可通过恰当地设置标志数组实现相应的线程同步，从而解决数据依赖问题.

3 算 例

3.1 并行测试

为了验证发展的针对隐式LU-SSOR方法的两种并行策略，选取展弦比为13.71的UH-1H桨叶进行测试.桨叶网格的大小为149(弦向)×41(法向)×81(展向)，背景网格的大小为241(周向)×81(纵向)×101(径向).计算在Intel(R)Xeon(R)CPU E5-2650 v3 @2.30GHZ服务器上进行，该服务器共有40个线程.

以一个扫描周期为例，利用超平面(Hyperplane)和管道流(Pipelining)两种方法对原有串行程序进行并行化处理，得到一个扫描周期内的耗时t(单位： s)随所用线程个数n(单位： 个)变化的关系图，如图4(见第592页).可以看出，当线程个数达到18时，并行加速比达到3.13，说明本文发展的两种并行策略使流场计算的效率得到大幅度提高,因此直升机旋翼噪声计算的周期大大缩减.

3.2 Caradonna-Tung旋翼有升力悬停

图4 超平面和管道流并行效果Fig.4 Parallel effects of hyperplane and pipelining

Caradonna-Tung旋翼[10]由两片桨叶组成，桨叶形状为矩形，展弦比为6，翼型为NACA0012，桨叶半径为1.143m，弦长19.05cm，翼型无扭转，无尖削.本算例的计算状态为： 桨尖马赫数为0.439，总距角为8°.

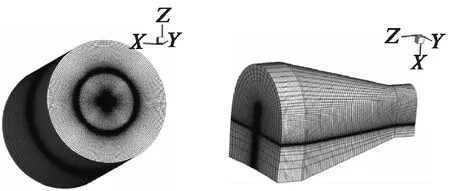
图5 背景网格(左)和桨叶网格(右)Fig.5 Background grid(left) and rotor mesh(right)

计算网格采用两块重叠网格，背景网格大小为221(周向)×121(纵向)×121(径向)，桨叶网格大小为121(弦向)×81(法向)×81(展向)，如图5所示.背景网格在周向均匀分布，在垂直方向于桨盘平面附近进行加密，径向在桨尖附近进行加密.旋翼桨叶网格的生成采用了双曲型网格生成方法[11]，只需要给定初始表面网格分布即可自动生成体网格.为了提高重叠网格的计算效率，避免旋翼桨叶网格在计算过程中出现重叠，外边界的大小沿展向从小到大分布.

本算例并行计算共耗时12.5h,而串行计算耗时39.9h,计算速度提高了3.2倍.图6给出了计算得到的不同展向位置翼型压力系数(CP)分布与试验值的对比，计算结果与试验值吻合很好，说明了本文发展的并行计算方法的准确性.

图6 不同展向位置翼型压力系数分布Fig.6 Distribution of pressure coefficients at different span positions

对该算例进行网格无关性分析，选取不同的网格数量级进行计算，如表1.图7给出了不同网格数量级计算得到的悬停拉力系数与NASA理论计算数值的对比，横坐标为网格数量n(万)，纵坐标为拉力系数CT.由图7可知，该算例当旋翼网格数量达到60万，背景网格数量达到200万时，计算收敛.

图7 悬停拉力系数与理论值对比Fig.7 Comparison of hover thrust coefficient with theoretical value

表1 旋翼网格和背景网格分布

注： 括号内的数值为网格的数量.

3.3 AH-1/OLS有升力前飞

AH-1/OLS模型旋翼[12-13]由两片桨叶组成，桨叶平面形状为矩形，桨叶带8.2°的线性负扭转，展弦比为9.22，静止状态下，在距离旋转中心75%展长处扭转角为0°，翼型为OLS翼型[14-15].桨叶在前飞过程中不仅有旋转运动，还包括挥舞、变距、摆振等运动.若定义旋翼桨叶的方位角为Ψ，变距角为θ，挥舞角为β，摆振角为δ，则桨叶的运动规律为：

ψ=ψ0+ωt,
β=β0+βlccos(ψ)+βlssin(ψ),
θ=θ0+θlccos(ψ)+θlssin(ψ),
δ=δ0+δlccos(ψ)+δlssin(ψ).

对AH-1/OLS旋翼的10014工况进行远场距离相关性分析，对应的计算状态为：

Mtip=0.664,μ=0.164,αTPP=1°,Re=1.6×106,CT=0.0054.

变距和挥舞运动规律如下：

θ(t)=6.14°+0.9°cos(ψ)-1.39°sin(ψ),
β(t)=0.5°+1.0°cos(ψ).

计算所用背景网格为圆柱形网格，在计算过程中也随桨叶做旋转运动.本文选取不同的远场距离进行了计算比较，如图8所示，r表示背景网格的半径，d表示背景网格的纵向长度.表2给出了4种计算状态和不同远场距离的拉力系数与试验值的误差，其中R为旋翼桨盘半径.由表可知随着远场距离的增大，计算收敛.

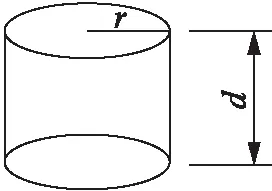
图8 远场边界示意图Fig.8 Far-field boundary schematic

表2 远场距离选择(a)和拉力系数的计算值与误差(b)

为了将数值计算的噪声与试验值作对比，选取该旋翼有噪声试验数据的3017工况进行噪声计算.3017工况的计算状态为：Mtip=0.663,μ=0.162,αTPP=1°,Re=1.6×106.变距运动规律为：

θ(t)=5.03°+1.98°cos(ψ)-2.04°sin(ψ).

选取旋翼控制面计算噪声.图9(见第594页)给出了旋翼控制面上的压强分布.图10(见第594页)给出了计算得到的噪声与试验值的对比，横坐标为方位角ψ，纵坐标为压力脉动p′，单位为Pa.计算结果与实验值吻合较好，说明本文发展的旋翼气动噪声数值预测方法的可靠性.在该工况下，串行计算耗时112.94h，并行计算耗时37.8h，计算速度提高了2.99倍.

图9 旋翼控制面上的压强分布示意图Fig.9 Diagram of pressure distribution on rotor control surface

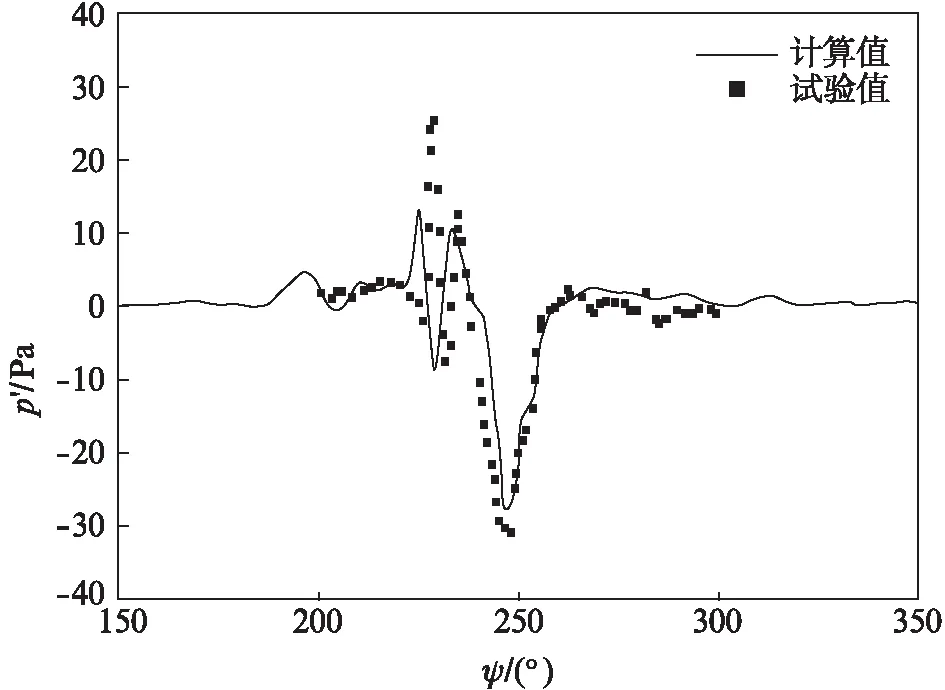
图10 计算噪声与试验值对比Fig.10 Comparison of calculated noise with test data

4 结 语

本文基于CFD/FW-H方法对旋翼的气动噪声进行了数值预测并基于OpenMP对源程序进行了并行优化.针对隐式LU-SSOR算法存在数据依赖性难以实现并行的问题，发展了超平面(Hyperplane)和管道流(Pipelining)两种并行策略，实现了LU-SSOR算法的OpenMP并行计算.算例显示，当并行计算的线程达到18时，两种并行策略使得旋翼涡流场的计算速度提高3倍以上.因此，旋翼噪声的计算周期大大缩短，说明本文发展的两种并行策略具有重要的工程应用价值.