探讨解未定式极限的方法

刘建峰，熊艳琴

（南京信息工程大学 数学与统计学院，江苏 南京 210044）

1 引言

极限是贯穿数学分析始终的基本问题，数学分析中的包括连续、导数、积分在内的几乎全部的基本概念都离不开极限.因此，极限运算是数学分析中十分重要的内容，而未定式极限是极限运算中的一个重要类型.未定式极限问题的出现还要早于极限理论[1]，甚至还要早于微积分的出现.早在16世纪就已经有了关于未定式极限的问题出现，比如求解瞬时速度就是求解一个型未定式极限.事实上，微积分处理的问题中的一部分——求导问题，就是一类型未定式极限问题.可以说，解决型未定式极限问题是微积分诞生的一个诱因.

未定式极限问题，本质上就是一类特殊的极限的四则运算问题.假设变量

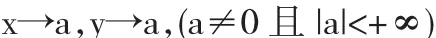
则变量x与变量y之间的四则运算都可以直接使用实数的四则运算法则，先对变量取极限，这时极限值就是一个实数，对实数就可以使用实数的四则运算法则，即极限运算与四则运算可以进行交换.但当a=0或a=∞时，情况出现了变化.极限取值不能简单确定，这也是未定式极限这一名称的由来.

求解未定式极限的最常用的方法是洛必达法则[2,3]，洛必达法则可以解决绝大多数的比式型的未定式极限，洛必达法则的出现是解决未定式极限问题的历史性的一刻.为了借用洛必达法则基本解决未定式极限问题，将其余非比式型的未定式极限转化为比式型的未定式极限也就显得十分必要了.

2 求解未定式极限的方法

方法一：约去0因式

定义1[1,2]若函数f(x)是由多个因式组成，函数u(x)满足，且 f(x)=u(x)f1(x)，则称 u(x)是 f(x)当 x→ω 时的一个0因式.若函数f1(x)同时满，称 u(x)是 f(x)当 x→ω时的全部0因式.

以v(x)=u(x)q(x)为例，则f(x)=u(x)f1(x),g(x)=v(x)g1(x)=u(x)q(x)g1(x)，从而

例1求极限

解原式

注：在运用约去0因式方法时，需要通过因式分解将分母的0因式分解出来，再与分子约分消去0因式.如果不能将分母的全部0因式约去，则约去0因式方法不能解决未定式极限问题.

方法二：等价无穷小替换

定义2[1,2]，则称当x→ω时u(x)是无穷小量.在此前提下，若，则称当 x→ω 时 u(x)和 v(x)是等价无穷小量，记为u(x)～v(x)(x→ω).

定理 1[1]若 u(x)～f(x)(x→ω).，则有：

下面通过一个例子来说明如何运用等价替换方法求解未定式极限.

例2求极限

解首先

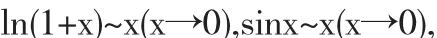
则有

可以看到，在解题的最后一步运用到了约去0因式方法，等价无穷小替换与约去0因式一般是相伴出现的.

注：等价无穷小替换一般不单独用来处理不定式极限，而是结合其他方法，通过等价替换将函数的结构变得简单同时，需要注意的是，在乘除运算中可以使用等价无穷小替换，但在加减运算中使用替换可能会导致错误.比如，我们来看下面一个例子.

例3求极限

解可以看到分母是一个差式，如果直接进行等价无穷小替换，则会得到如下结果

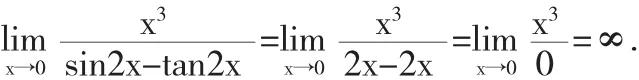
但实际上

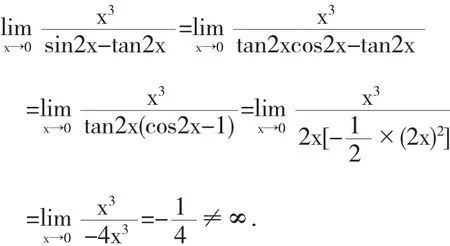
方法三：洛必达法则

定理2[2,3]对于极限，当函数 f(x)和 g(x)在 U0(ω)上可导，且g'(x)≠0时.若此时有

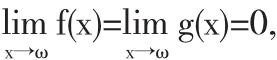
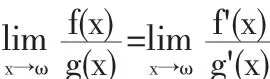
例4求极限

解显然，该极限是型未定式极限，运用洛必达法则，有

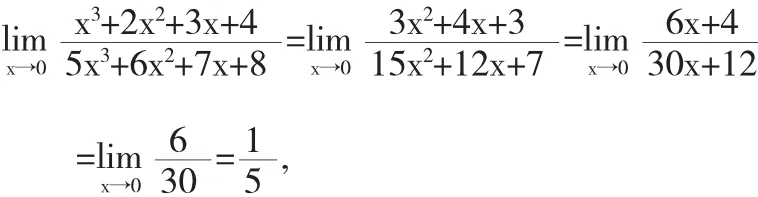
例5求极限

解显然，该极限是型未定式极限，反复运用洛必达法则得到

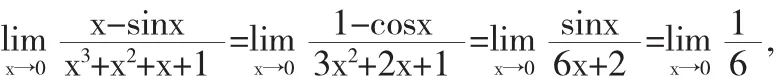
方法四：泰勒公式

定理3[1,2,4]设函数f(x)在ω处有n阶导数，则存在ω的一个邻域 u(ω)，任意 x∈U(ω)，有

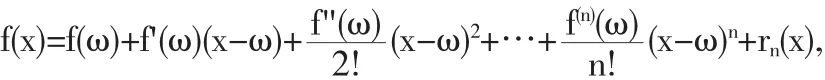
称rn(x)为Peano余项，且满足

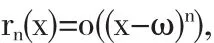
前n+1项组成的多项式

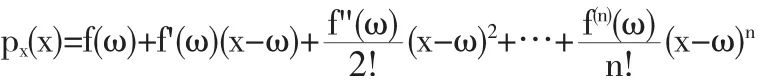
称为f(x)的n次Taylor多项式.

上述公式称为f(x)在x=ω处的带Peano余项的Taylor公式.

例6求极限

解将在x=0处展开

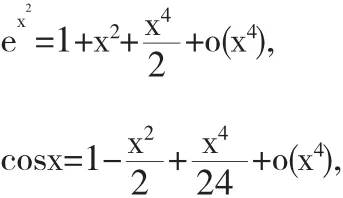
代入极限，得

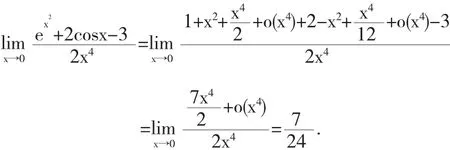
例7求极限

解若对这个未定式极限直接运用泰勒公式，需要将函数与sin2x在x=0处展开到5阶，即将函数ln展开到5阶，有

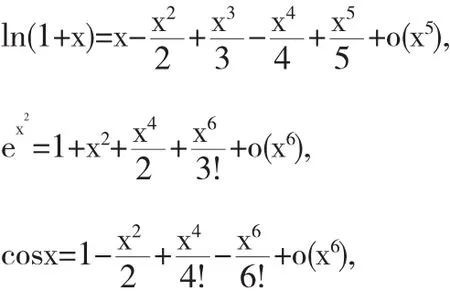
代入极限，得

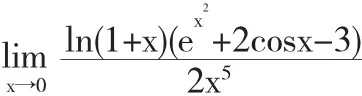
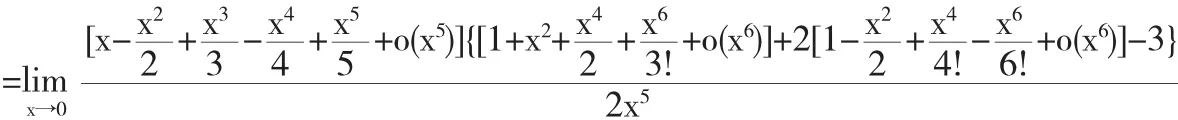
这样计算十分繁琐，但若在运用泰勒公式之前先运用约去0因式与等价无穷小替换的方法，就可以大大简化计算.

首先

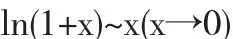
则有

分子、分母同时约去0因式x，得到极限

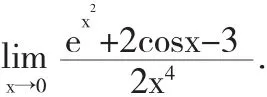
可以发现，在运用了约去0因式与等价无穷小替换方法之后，原本较复杂的未定式极限化为了较易处理的极限，极限的求解过程在例6中已经给出.

3 求解未定式极限方法之间的联系

3.1 约去0因式与等价无穷小替换之间的联系

约去0因式要求分母得0因式能够和分子约分消去，但这一要求比较高，而等价无穷小替换能够为约去0因式服务，使得分母得0因式被约去的概率大大提高.同时若在等价无穷小替换之后不进行约去0因式，则等价无穷小替换的操作就没有了意义，等价无穷小替换之后必然进行约去0因式.这两种方法往往相伴出现.

3.2 等价无穷小替换与泰勒公式之间的联系

等价无穷小替换，本质上就是略去尾式后的在x=0处的泰勒公式.参考等价无穷小替换

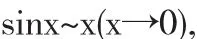
sinx在x=0处的泰勒公式为

令两端 x→0，略去 o(x)，得

即sinx的等价无穷小替换

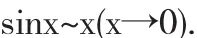
3.3 洛必达法则与泰勒公式之间的联系

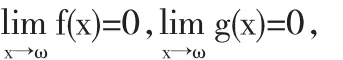
将函数f(x)和g(x)在x=ω处进行泰勒展开，得

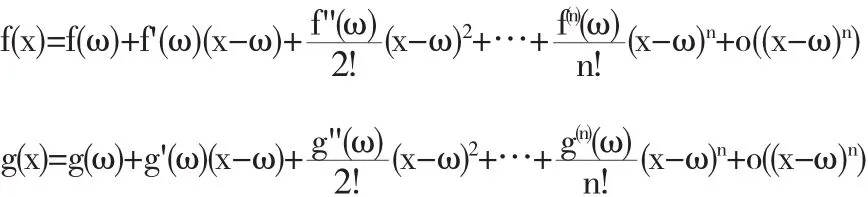
两端令x→ω，得

故

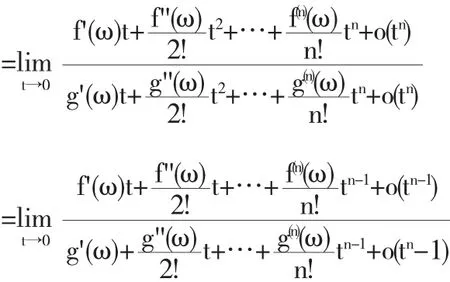
当 g'(ω)≠0 时，且函数 f'(x)和 g'(x)在 U(ω)上连续，则有

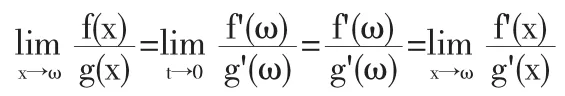
即运用一次洛必达法则.

当 g"(ω)≠0 时，且函数 f"(x)和 g"(x)在 U(ω)上连续，则有

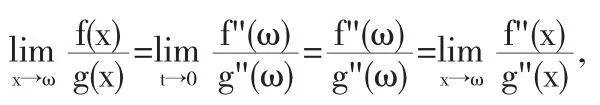
即反复运用两次洛必达法则.

此后反复以上步骤，可发现泰勒公式是洛必达法则的核心，是洛必达法则的本质，在运用上相比与洛必达法则较为复杂，但使用范围更广.